Skip to main content

Advertisement

SpringerLink
Log in

Upper primary school teachers’ mathematical knowledge for teaching functional thinking in algebra

  • Published:
Journal of Mathematics Teacher Education Aims and scope Submit manuscript

Abstract

This article is based on a project that investigated teachers’ knowledge in teaching an important aspect of algebra in the middle years of schooling—functions, relations and joint variation. As part of the project, 105 upper primary teachers were surveyed during their participation in Contemporary Teaching and Learning of Mathematics, a research project funded by the Catholic Education Office, Melbourne (2008–2012). Analysis of the survey responses revealed that two-thirds of teachers demonstrated content knowledge on a pattern generalisation task appropriate for upper primary levels of schooling (8- to 12-year-old students), but less than half demonstrated reasonable pedagogical content knowledge (PCK). On a paired variable (function machine) task, only one quarter of teachers demonstrated appropriate PCK. Although two-thirds of the teachers indicated that they currently taught content from the “Patterns and Algebra” strand of the new Australian Curriculum, less than half were able to provide examples of appropriate learning experiences for students. More than two-thirds of teachers expressed concern about their ability to teach this area of mathematics. Implications for the professional learning of teachers to improve their mathematics knowledge for developing students’ functional thinking are presented.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2

Similar content being viewed by others

Notes

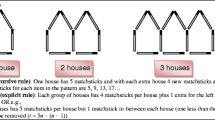
  1. Such a procedure might be as follows: ‘the ‘jump’ between consecutive numbers in the sequence is the number that goes before the ‘n’ (4 for the caterpillar pattern) and then you add or take away another number to adjust the ‘n’ term get the rule’ (‘+2’ in the case of the caterpillar pattern to get ‘4n + 2’). The author has seen this procedure outlined in secondary mathematics textbooks.

References

  • Adler, J., Davis, Z., Kazima, M., Parker, D., & Webb, L. (2005). Working with learners’ mathematics: Exploring a key element of mathematical knowledge for teaching. In H. Chick & J. L. Vincent (Eds.), Proceedings of the 29th Conference of the International Group for the Psychology of Mathematics Education (Vol. 2, pp. 1–8). Melbourne, Australia: PME.

  • Australian Council for Educational Research. (2010). Released items: Future teacher mathematics content knowledge (MCK) and mathematics pedagogical content knowledge (MPCK)—Primary: TEDS-M International Study Center. East Lansing, USA: Michigan State University.

    Google Scholar 

  • Australian Curriculum Assessment and Reporting Authority. (2009, January, 2011). The Australian curriculum: Mathematics Retrieved October 1, 2011, from http://www.australiancurriculum.edu.au/Mathematics/Curriculum/F-10.

  • Ball, D. L., & Bass, H. (2000). Interweaving content and pedagogy in teaching and learning to teach: Knowing and using mathematics. In J. Boaler (Ed.), Multiple perspectives on the teaching and learning of mathematics (pp. 83–104). Westport, CT: Ablex.

    Google Scholar 

  • Ball, D. L., Hill, H. C., & Bass, H. (2005). Knowing mathematics for teaching: Who knows mathematics well enough to teach third grade, and how can we decide? (pp. 14–46). Fall: American Educator.

    Google Scholar 

  • Ball, D. L., Thames, M. H., & Phelps, G. (2008). Content knowledge for teaching: What makes it special? Journal of Teacher Education, 59(5), 389–407.

    Article  Google Scholar 

  • Blanton, M. L., & Kaput, J. J. (2008). Building district capacity for teacher development in algebraic reasoning. In J. L. Kaput, D. W. Carraher, & M. L. Blanton (Eds.), Algebra in the early grades (pp. 361–388). New York: Taylor & Francis Group.

    Google Scholar 

  • Cai, J., & Moyer, J. (2008). Developing algebraic thinking in earlier grades: Some insights from international comparative studies. In C. Greenes & R. Rubenstein (Eds.), Algebra and algebraic thinking in school mathematics (pp. 169–180). Reston, VA: The National Council of Teachers of Mathematics.

    Google Scholar 

  • Carpenter, T. P., Fennema, E., Peterson, P. L., Chiang, C.-P., & Loef, M. (1989). Using knowledge of children’s mathematics thinking in classroom teaching: An experimental study. American Educational Research Journal, 26(4), 499–531.

    Article  Google Scholar 

  • Carraher, D. W., Schliemann, A. D., Brizuela, B. M., & Earnest, D. (2006). Arithmetic and algebra in early mathematics education. Journal for Research in Mathematics Education, 37(2), 87–115.

    Google Scholar 

  • Cobb, P. (2000). Conducting teaching experiments in collaboration with teachers. In A. E. Kelly & R. A. Lesh (Eds.), Handbook of research design in mathematics and science education (pp. 307–333). Mahwah, NJ: Lawrence Erlbaum Associates.

    Google Scholar 

  • Confrey, J., & Smith, E. (1994). Exponential functions, rates of change, and the multiplicative unit. Educational Studies in Mathematics, 26(2/3), 135–164.

    Article  Google Scholar 

  • Creswell, J. W. (2007). Qualitative inquiry and research design: Choosing among five approaches (2nd ed.). Thousand Oaks, CA: Sage.

    Google Scholar 

  • Downton, A., Knight, R., Clarke, D., & Lewis, G. (2006). Mathematics assessment for learning: Rich tasks & work samples. Melbourne: Mathematics Teaching and Learning Centre, Australian Catholic University.

    Google Scholar 

  • Driscoll, M. (1999). Fostering algebraic thinking: A guide for teachers, grades 6–10. Portsmouth, NH: Heinemann.

    Google Scholar 

  • English, L. D., & Warren, E. (1998). Introducing the variable through pattern exploration. The Mathematics Teacher, 91(2), 166–170.

    Google Scholar 

  • Friel, S. N., & Markworth, K. A. (2009). A framework for analyzing geometric pattern tasks. Mathematics Teaching in the Middle School, 15(1), 24–33.

    Google Scholar 

  • Goulding, M., Rowland, T., & Barber, P. (2002). Does it matter? Primary teacher trainees’ subject knowledge in mathematics. British Educational Research Journal, 28(5), 689–704.

    Article  Google Scholar 

  • Greenes, C., Cavanagh, M., Dacey, L., Findell, C., & Small, M. (2001). Navigating through algebra in prekindergarten—grade 2. Reston, VA: The National Council of Teachers of Mathematics.

    Google Scholar 

  • Hadjidemetriou, C., & Williams, J. (2002). Teachers’ pedagogical content knowledge: Graphs from a cognitivist to a situated perspective. In A. D. Cockburn & E. Nardi (Eds.), Proceedings of the 26th PME International Conference (Vol. 3, pp. 57–64).

  • Hill, H., Ball, D. L., & Schilling, S. G. (2008). Unpacking pedagogical content knowledge: Conceptualising and measuring teachers’ topic-specific knowledge of students. Journal for Research in Mathematics Education, 39(4), 372–400.

    Google Scholar 

  • Hodgen, J., Küchemann, D., & Brown, M. (2010). Textbooks for the teaching of algebra in lower secondary school: Are they informed by research? PEDAGOGIES, 5(3), 187–201.

    Article  Google Scholar 

  • Jacobs, V. R., Lamb, L. L. C., & Philipp, R. A. (2010). Professional noticing of children’s mathematical thinking. Journal for Research in Mathematics Education, 41(2), 169–202.

    Google Scholar 

  • Kaput, J. J. (1999). Teaching and learning a new algebra. In E. Fennema & T. Romberg (Eds.), Mathematics classrooms that promote understanding (pp. 133–155). Mahwah, NJ: Erlbaum.

    Google Scholar 

  • Kaput, J. J. (2008). What is algebra? What is algebraic reasoning? In J. L. Kaput, D. W. Carraher, & M. L. Blanton (Eds.), Algebra in the early grades (pp. 5–17). New York: Taylor & Francis Group.

    Google Scholar 

  • Kieran, C. (2004). Algebraic thinking in the early grades: What Is It? The Mathematics Educator, 8(1), 139–151.

    Google Scholar 

  • Kruteskii, V. (1976). The psychology of mathematical ability in school children. Chicago: University of Chicago Press.

    Google Scholar 

  • Kuchemann, D. (2010). Using patterns generically to see structure. PEDAGOGIES, 5(3), 233–250.

    Article  Google Scholar 

  • Lee, L., & Freiman, V. (2004). Tracking primary students’ understanding of patterns. Paper presented at the Annual Meeting—Psychology of Mathematics & Education of North America, Toronto, CA.

  • Lins, R., & Kaput, J. J. (2004). The early development of algebraic reasoning: The current state of the field. In K. Stacey, H. Chick, & M. Kendal (Eds.), The future of the teaching and learning of algebra (pp. 47–70). Boston: Kluwer Academic Publishers.

    Google Scholar 

  • MacGregor, M., & Stacey, K. (1995). The effect of different approaches to algebra on students’ perceptions of functional relationships. Mathematics Education Research Journal, 7(1), 69–85.

    Article  Google Scholar 

  • Markworth, K. A. (2010). Growing and growing: Promoting functional thinking with geometric growing patterns. Unpublished PhD, University of North Carolina at Chapel Hill, Chapel Hill.

  • Mason, J. (1996). Expressing generality and roots of algebra. In N. Bednarz, C. Kieran, & L. Lee (Eds.), Approaches to algebra: Perspectives for research and teaching (pp. 65–86). Dordrecht: Kluwer Academic Publishers.

    Chapter  Google Scholar 

  • Menzel, B., & Clarke, D. (1999). Teacher mediation of student construction of algebra knowledge. In J. M. Truran & K. M. Truran (Eds.), Proceedings of the twenty-second annual conference of The Mathematics Education Research Group of Australasia Incorporated, held in Adelaide, South Australia, 4–7 July (pp. 365–372): MERGA.

  • Moss, J., Beatty, R., Barkin, S., & Shillolo, G. (2008). “What is your theory? What is your rule? Fourth graders build an understanding of function through patterns and generalising problems. In C. Greenes & R. Rubenstein (Eds.), Algebra and algebraic thinking in school mathematics (pp. 155–168): National Council of Teachers of Mathematics.

  • Mullis, I. V. S., Martin, M. O., Gonzalez, E. J., & Chrostowski, S. J. (2004). TIMSS 2003 international mathematics report: Lynch school of education. Boston College: TIMSS and PIRLS International Study Center.

    Google Scholar 

  • Nathan, M. J., & Koellner, K. (2007). A framework for understanding and cultivating the transition from arithmetic to algebraic reasoning. Mathematical Thinking & Learning, 9(3), 179–192.

    Article  Google Scholar 

  • Nathan, M. J., & Petrosino, A. (2003). Expert blind spot among preservice teachers. American Educational Research Journal, 40(4), 905–928.

    Article  Google Scholar 

  • National Council of Teachers of Mathematics. (2000). Principles and standards for school mathematics. Reston, VA: NCTM.

    Google Scholar 

  • O’Toole, J., & Beckett, D. (2010). Educational research: Creative thinking & doing. Melbourne: Oxford University Press.

    Google Scholar 

  • Rivera, F. (2010). Visual templates in pattern generalization activity. Educational Studies in Mathematics, 73(3), 297–328.

    Article  Google Scholar 

  • Roche, A., & Clarke, D. (2011). Some lessons learned from the experience of assessing teacher pedagogical content knowledge in mathematics. In J. Clark, B. Kissane, J. Mousley, T. Spencer & S. Thornton (Eds.), Mathematics traditions and [new] practices: Proceedings of the 23rd biennial conference of the Australian Association of Mathematics Teachers Inc. and the 34th annual conference of the Mathematics Education Research Group of Australasia Inc., (Vol. 2, pp. 658–666). Adelaide: MERGA.

  • Rule, A., & Hallagan, J. (2007). Using hands-on materials to write algebraic generalizations (grades 5–8). Paper presented at the Annual Conference of the Association of Mathematics Teachers of New York State.

  • Saul, M. (2008). Algebra: The mathematics and the pedagogy. In C. Greenes & R. Rubenstein (Eds.), Algebra and algebraic thinking in school mathematics (pp. 63–79). Reston, VA: The National Council of Teachers of Mathematics.

    Google Scholar 

  • Senk, S., Tatto, M., Reckase, M., Rowley, G., Peck, R., & Bankov, K. (2012). Knowledge of future primary teachers for teaching mathematics: An international comparative study. ZDM (Online first), (pp. 1–18).

  • Shulman, L. S. (1986). Those who understand: Knowledge growth in teaching. Educational Researcher, 15(2), 4–14.

    Article  Google Scholar 

  • Skemp, R. (2002). Instrumental and relational understanding. In D. Tall & M. Thomas (Eds.), Intelligence, learning and understanding in mathematics : A tribute to Richard Skemp. Flaxton, QLD: Post Pressed.

    Google Scholar 

  • Smith, E. (2008). Representational thinking as a framework for introducing functions in the elementary curriculum. In J. L. Kaput, D. W. Carraher, & M. L. Blanton (Eds.), Algebra in the early grades (pp. 133–160). New York: Taylor & Francis Group.

    Google Scholar 

  • Stacey, K. (1989). Finding and using patterns in linear generalising problems. Educational Studies in Mathematics, 20(2), 147–164.

    Article  Google Scholar 

  • Stacey, K., & Chick, H. (2004). What is the problem with algebra? In K. Stacey, H. Chick, & M. Kendal (Eds.), The future of the teaching and learning of algebra (pp. 1–20). Boston: Kluwer Academic Publishers.

    Google Scholar 

  • Tatto, M. T., Schwille, J., Senk, S. L., Ingvarson, L., Rowley, G., Peck, R., et al. (2012). Policy, practice, and readiness to teach primary and secondary mathematics in 17 countries: Findings from the IEA Teacher Education and Development Study in Mathematics (TEDS-M). Amsterdam, The Netherlands: International Association for the Evaluation of Educational Achievement.

    Google Scholar 

  • Usiskin, Z. (1988). Conceptions of school algebra and uses of variables. In A. F. Coxford & A. P. Shulte (Eds.), The ideas of algebra, K-12: NCTM 1988 Yearbook (pp. 8–19). Reston, VA: National Council of Teachers of Mathematics.

    Google Scholar 

  • Victorian Curriculum and Assessment Authority. (2007, February 22, 2011). Victorian Essential Learning Standards: Mathematics Retrieved May 2, 2012, from http://vels.vcaa.vic.edu.au/vels/maths.html.

  • Warren, E. (2000). Visualisation and the development of early understanding in algebra. Paper presented at the 24th Conference of the International Group for the Psychology of Mathematics Education (PME), Hiroshima, Japan.

  • Warren, E., & Cooper, T. (2008). Generalising the pattern rule for visual growth patterns: Actions that support 8 year olds’ thinking. Educational Studies in Mathematics, 67(2), 171–185.

    Article  Google Scholar 

  • Wright, V. (1997). Assessing mathematical processes in algebra. Unpublished Research dissertation. University of Waikato.

Download references

Acknowledgments

The author would like to acknowledge with appreciation the teacher participants from the Contemporary Teaching and Learning of Mathematics project who contributed to the study on which this article is based. I am indebted to Anne Roche and Associate Professor Vince Wright for their helpful feedback on data instrumentation and participation in the check-scoring process.

Author information

Authors and Affiliations

  1. Mathematics Teaching and Learning Research Centre, Australian Catholic University, 115 Victoria Parade, Fitzroy, Locked Bag 4115, Melbourne, VIC, 3065, Australia

    Karina J. Wilkie

Authors
  1. Karina J. Wilkie
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Karina J. Wilkie.

Appendix: Questionnaire

Appendix: Questionnaire

figure a
figure b
figure c

Rights and permissions

Reprints and permissions

About this article

Cite this article

Wilkie, K.J. Upper primary school teachers’ mathematical knowledge for teaching functional thinking in algebra. J Math Teacher Educ 17, 397–428 (2014). https://doi.org/10.1007/s10857-013-9251-6

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10857-013-9251-6

Keywords

Search

Navigation