Skip to main content
SpringerLink
Log in

Multiphysics modeling and analysis of laminated composites with interfacial imperfections in thermal environments

  • The Physics of Metal Plasticity: in honor of Professor Hussein Zbib
  • Published:
Journal of Materials Science Aims and scope Submit manuscript

Abstract

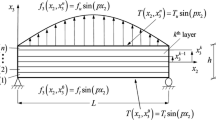
This work presents novel three-dimensional solutions for the multiphysics response of magneto-electro-elastic multilayered plates with interfacial imperfections in a thermal environment. The Stroh formalism is employed, incorporating thermal coupling with the Eringen nonlocal theory to capture small-scale effects. The laminated structures are simply supported and subjected to time-harmonic temperature distributions and extended tractions represented using Fourier series expansions. The dual variable and position technique is used to address the challenges posed by non-ideal thermal and mechanical bonded contacts between constituents, ensuring the consistency and stability of the recursive field relations. A wide range of application examples are analyzed, including the influence of material arrangements, aspect ratio and nonlocal length characteristics, elastically compliant and thermally/dielectrically weakly conducting interfaces, as well as forced vibrations in combined thermo-mechanical environments. The comprehensive results shed light on the intricate multiphysics response of multilayered structures and provide valuable insights into practical engineering implications for advanced materials and structures.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Figure 1
Figure 2
Figure 3
Figure 4
Figure 5
Figure 6
Figure 7

Similar content being viewed by others

Data availibility

Data and code are available upon request.

References

  1. Basheer A (2020) Advances in the smart materials applications in the aerospace industries. Aircr Eng Aerosp Technol 92:1027–1035

    Google Scholar 

  2. Rocha H, Semprimoschnig C, Nunes JP (2021) Sensors for process and structural health monitoring of aerospace composites: a review. Eng Struct 237:112231

    Google Scholar 

  3. Wang W, Xiang Y, Yu J, Yang L (2023) Development and prospect of smart materials and structures for aerospace sensing systems and applications. Sensors 23:1545

    PubMed  PubMed Central  Google Scholar 

  4. Heyliger PR, Ramirez G, Saravanos D (1994) Coupled discrete-layer finite element models for laminated piezoelectric plates. Commun Numer Methods Eng 10:971–981

    Google Scholar 

  5. Heyliger PR, Ramirez F, Pan E (2004) Two-dimensional static fields in magnetoelectroelastic laminates. J Intell Mater Syst Struct 15:689–709

    Google Scholar 

  6. Ramirez F, Heyliger PR, Pan E (2006) Static analysis of functionally graded elastic anisotropic plates using a discrete layer approach. Compos Part B Eng 37:10–20

    Google Scholar 

  7. Ramirez F, Heyliger PR, Pan E (2006) Free vibration response of two-dimensional magneto-electro-elastic laminated plates. J Sound Vib 292:626–644

    Google Scholar 

  8. Ramirez F, Heyliger PR, Pan E (2006) Discrete layer solution to free vibrations of functionally graded magneto-electro-elastic plates. Mech Adv Mater Struct 13:249–266

    CAS  Google Scholar 

  9. Carrera E, Brischetto S, Fagiano C, Nali P (2009) Mixed multilayered plate elements for coupled magneto-electro-elastic analysis. Multidiscip Model Mater Struct 5:251–256

    Google Scholar 

  10. Milazzo A (2014) Layer-wise and equivalent single layer models for smart multilayered plates. Compos Part B Eng 67:62–75

    Google Scholar 

  11. Filippi M, Giusa D, Pagani A, Zappino E, Carrera E (2020) Assessment of classical, advanced, and layer-wise theories for the vibration of rotating composite anisotropic blades. Compos Struct 245:112315

    Google Scholar 

  12. Najafi M, Ahmadi I (2022) Nonlocal layerwise theory for bending, buckling and vibration analysis of functionally graded nanobeams. Eng Comput 39:2653–2675

    Google Scholar 

  13. Sladek J, Sladek V, Krahulec S, Pan E (2013) The MLPG analyses of large deflections of magnetoelectroelastic plates. Eng Anal Bound Elem 37:673–682

    Google Scholar 

  14. Sladek J, Sladek V, Chen CS, Young DL (2014) Analysis of circular magnetoelectroelastic plates with functionally graded material properties. Mech Adv Mater Struct 22:479–489

    Google Scholar 

  15. Khorasani VS, Żur KK, Kim J, Reddy JN (2022) On the dynamics and stability of size-dependent symmetric FGM plates with electro-elastic coupling using meshless local Petrov-Galerkin method. Compos Struct 298:115993

    Google Scholar 

  16. Buchanan GR (2004) Layered versus multiphase magneto-electro-elastic composites. Compos Part B Eng 35:413–420

    Google Scholar 

  17. Bhangale RK, Ganesan N (2006) Static analysis of simply supported functionally graded and layered magneto-electro-elastic plates. Int J Solids Struct 43:3230–3253

    CAS  Google Scholar 

  18. Annigeri AR, Ganesan N, Swarnamani S (2007) Free vibration behavior of multiphase and layered magneto-electro-elastic beam. J Sound Vib 299:44–63

    Google Scholar 

  19. Milazzo A, Orlando C (2012) A beam finite element for magneto-electro-elastic multilayered composite structures. Compos Struct 94:3710–3721

    Google Scholar 

  20. Kiran MC, Kattimani SC (2018) Assessment of porosity influence on vibration and static behaviour of functionally graded magneto-electro-elastic plate: A finite element study. Eur J Mech A/Solids 71:258–277

    Google Scholar 

  21. Vinyas M (2019) A higher-order free vibration analysis of carbon nanotube-reinforced magneto-electro-elastic plates using finite element methods. Compos Part B Eng 158:286–301

    CAS  Google Scholar 

  22. Zhou L, Li M, Tang J, Li F, Żur KK (2021) Evaluation of performance of magneto-electro-elastic sensor subjected to thermal-moisture coupled load via CS-FEM. Thin-Walled Struct 169:108370

    Google Scholar 

  23. Zhou L, Wang J, Liu M, Li M, Chai Y (2022) Evaluation of the transient performance of magneto-electro-elastic based structures with the enriched finite element method. Compos Struct 280:114888

    Google Scholar 

  24. Wang J, Chen L, Fang S (2002) State vector approach to analysis of multilayered magneto-electro-elastic plates. Int J Solids Struct 40:1669–1680

    Google Scholar 

  25. Chen J, Pan E, Chen H (2007) Wave propagation in magneto-electro-elastic multilayered plates. Int J Solids Struct 44:1073–1085

    CAS  Google Scholar 

  26. Xin L, Hu Z (2015) Free vibration of simply supported and multilayered magneto-electro-elastic plates. Compos Struct 121:344–350

    Google Scholar 

  27. Pan E (2001) Exact solution for simply supported and multilayered magneto-electro-elastic plates. J Appl Mech 68:608–618

    CAS  Google Scholar 

  28. Pan E, Heyliger P (2002) Free vibrations of simply supported and multilayered magneto-electro-elastic plates. J Sound Vib 252:429–442

    Google Scholar 

  29. Wang Y, Xu R, Ding H, Chen J (2010) Three-dimensional exact solutions for free vibrations of simply supported magneto-electro-elastic cylindrical panels. Int J Eng Sci 48:1778–1796

    Google Scholar 

  30. Waksmanski N, Pan E (2014) An analytical three-dimensional solution for free vibration of a magneto-electro-elastic plate considering the nonlocal effect. J Intell Mater Syst Struct 28:1501–1513

    Google Scholar 

  31. Gohari S, Sharifi S, Vrcelj Z (2016) New explicit solution for static shape control of smart laminated cantilever piezo-composite-hybrid plates/beams under thermo-electro-mechanical loads using piezoelectric actuators. Compos Struct 145:89–112

    Google Scholar 

  32. Pan E, Waksmanski N (2016) Deformation of a layered magnetoelectroelastic simply-supported plate with nonlocal effect, an analytical three-dimensional solution. Smart Mater Struct 25:095013

    Google Scholar 

  33. Gohari S, Sharifi S, Vrcelj Z (2017) A novel explicit solution for twisting control of smart laminated cantilever composite plates/beams using inclined piezoelectric actuators. Compos Struct 161:477–504

    Google Scholar 

  34. Guo J, Sun T, Pan E (2019) Three-dimensional buckling of embedded multilayered magnetoelectroelastic nanoplates/graphene sheets with nonlocal effect. J Intell Mater Syst Struct 30:2870–2893

    CAS  Google Scholar 

  35. Dat ND, Quan TQ, Mahesh V, Duc ND (2020) Analytical solutions for nonlinear magneto-electro-elastic vibration of smart sandwich plate with carbon nanotube reinforced nanocomposite core in hygrothermal environment. Int J Mech Sci 186:105906

    Google Scholar 

  36. Sui Y, Wang W, Zhang H (2022) Effects of electromagnetic fields on the contact of magneto-electro-elastic materials. Int J Mech Sci 223:107283

    Google Scholar 

  37. Del Toro R, Bacigalupo A, Lepidi M, Mazzino A (2022) Dispersive waves in magneto-electro-elastic periodic waveguides. Int J Mech Sci 236:107759

    Google Scholar 

  38. Malikan M, Eremeyev VA (2023) On dynamic modeling of piezomagnetic/flexomagnetic microstructures based on Lord-Shulman thermoelastic model. Arch Appl Mech 93:181–196

    Google Scholar 

  39. Li YS, Cai ZY, Shi SY (2014) Buckling and free vibration of magnetoelectroelastic nanoplate based on nonlocal theory. Compos Struct 111:522–529

    Google Scholar 

  40. Nami MR, Janghorban M (2014) Resonance behavior of FG rectangular micro/nano plate based on nonlocal elasticity theory and strain gradient theory with one gradient constant. Compos Struct 111:349–353

    Google Scholar 

  41. Daneshmehr A, Rajabpoor A, Hadi A (2015) Size dependent free vibration analysis of nanoplates made of functionally graded materials based on nonlocal elasticity theory with high order theories. Int J Eng Sci 95:23–35

    Google Scholar 

  42. Li S, Pan E (2015) Static bending and free vibration of a functionally graded piezoelectric microplate based on the modified couple-stress theory. Int J Eng Sci 97:40–59

    CAS  Google Scholar 

  43. Farajpour A, Hairi Yazdi MR, Rastgoo A, Loghmani A, Mohammadi M (2016) Nonlocal nonlinear plate model for large amplitude vibration of magneto-electro-elastic nanoplates. Compos Struct 140:323–336

    Google Scholar 

  44. Arefi M, Zenkour AM (2017) Wave propagation analysis of a functionally graded magneto-electro-elastic nanobeam rest on Visco-Pasternak foundation. Mech Res Commun 79:51–62

    Google Scholar 

  45. Zhang DP, Lei YJ, Shen ZB (2017) Thermo-electro-mechanical vibration analysis of piezoelectric nanoplates resting on viscoelastic foundation with various boundary conditions. Int J Mech Sci 131–132:1001–1015

    Google Scholar 

  46. Barati MR (2018) A general nonlocal stress-strain gradient theory for forced vibration analysis of heterogeneous porous nanoplates. Eur J Mech A/Solids 67:215–230

    Google Scholar 

  47. Ma LH, Ke LL, Reddy JN, Yang J, Kitipornchai S, Wang YS (2018) Wave propagation characteristics in magneto-electro-elastic nanoshells using nonlocal strain gradient theory. Compos Struct 199:10–23

    Google Scholar 

  48. Barretta R, Faghidian SA, de Sciarra FM (2019) Stress-driven nonlocal integral elasticity for axisymmetric nano-plates. Int J Eng Sci 136:38–52

    Google Scholar 

  49. Karami B, Janghorban M, Rabczuk T (2019) Static analysis of functionally graded anisotropic nanoplates using nonlocal strain gradient theory. Compos Struct 227:111249

    Google Scholar 

  50. Liu H, Lyu Z (2020) Modeling of novel nanoscale mass sensor made of smart FG magneto-electro-elastic nanofilm integrated with graphene layers. Thin-Wall Struct 151:106749

    Google Scholar 

  51. Moayedi H, Ebrahimi F, Habibi M, Safarpour H, Foong LK (2020) Application of nonlocal strain-stress gradient theory and GDQEM for thermo-vibration responses of a laminated composite nanoshell. Eng Comput 37:3359–3374

    Google Scholar 

  52. Thai CH, Ferreira AJM, Phung-Van P (2020) Free vibration analysis of functionally graded anisotropic microplates using modified strain gradient theory. Eng Anal Bound Elem 117:284–298

    Google Scholar 

  53. Żur KK, Arefi M, Kim J, Reddy JN (2020) Free vibration and buckling analyses of magneto-electro-elastic FGM nanoplates based on nonlocal modified higher-order sinusoidal shear deformation theory. ComposPart B Eng 182:107601

    Google Scholar 

  54. Ebrahimi F, Karimiasl M, Singhal A (2021) Magneto-electro-elastic analysis of piezoelectric-flexoelectric nanobeams rested on silica aerogel foundation. Eng Comput 37:1007–1014

    Google Scholar 

  55. Wang X, Jin F et al (2022) Jin F Shear horizontal wave propagation in multilayered magneto-electro-elastic nanoplates with consideration of surface/interface effects and nonlocal effects. Wavesin Random and Complex Media. https://doi.org/10.1080/17455030.2022.2134599

    Article  Google Scholar 

  56. Karami B, Ghayesh MH (2023) Vibration characteristics of sandwich microshells with porous functionally graded face sheets. Int J Eng Sci 189:103884

    Google Scholar 

  57. Kumaravel A, Ganesan N, Sethuraman R (2007) Steady-state analysis of a three-layered electro-magneto-elastic strip in a thermal environment. Smart Mater Struct 16:282–295

    CAS  Google Scholar 

  58. Boroujerdy MS, Eslami MR (2013) Nonlinear axisymmetric thermomechanical response of piezo-FGM shallow spherical shells. Arch Appl Mech 83:1681–1693

    Google Scholar 

  59. Ke LL, Wang YS, Reddy JN (2014) Thermo-electro-mechanical vibration of size-dependent piezoelectric cylindrical nanoshells under various boundary conditions. Compos Struct 116:626–636

    Google Scholar 

  60. Ansari R, Gholami R, Rouhi H (2015) Size-dependent nonlinear forced vibration analysis of magneto-electro-thermo-elastic Timoshenko nanobeams based upon the nonlocal elasticity theory. Compos Struct 126:216–226

    Google Scholar 

  61. Shen HS, Xiang Y (2015) Thermal postbuckling of nanotube-reinforced composite cylindrical panels resting on elastic foundations. Compos Struct 123:383–392

    Google Scholar 

  62. Ebrahimi F, Barati MR (2016) Dynamic modeling of a thermo-piezo-electrically actuated nanosize beam subjected to a magnetic field. Appl Phys A 122:451

    Google Scholar 

  63. Mohammadimehr M, Salemi M, Rousta Navi B (2016) Bending, buckling, and free vibration analysis of MSGT microcomposite Reddy plate reinforced by FG-SWCNTs with temperature-dependent material properties under hydro-thermo-mechanical loadings using DQM. Compos Struct 138:361–380

    Google Scholar 

  64. Wang KF, Wang B, Zhang C (2016) Surface energy and thermal stress effect on nonlinear vibration of electrostatically actuated circular micro-/nanoplates based on modified couple stress theory. Acta Mech 228:129–140

    Google Scholar 

  65. Gholami R, Ansari R, Gholami Y (2017) Size-dependent bending, buckling and vibration of higher-order shear deformable magneto-electro-thermo-elastic rectangular nanoplates. Mater Res Exp 4:065702

    Google Scholar 

  66. Mahesh V, Sagar PJ, Kattimani S (2017) Influence of coupled fields on free vibration and static behavior of functionally graded magneto-electro-thermo-elastic plate. J Intell Mater Syst Struct 29:1430–1455

    Google Scholar 

  67. Vinyas M, Kattimani SC (2018) Investigation of the effect of BaTiO3/CoFe2O4 particle arrangement on the static response of magneto-electro-thermo-elastic plates. Compos Struct 185:51–64

    Google Scholar 

  68. Shojaeefard MH, Mahinzare M, Safarpour H, Saeidi Googarchin H, Ghadiri H (2018) Free vibration of an ultra-fast-rotating-induced cylindrical nano-shell resting on a Winkler foundation under thermo-electro-magneto-elastic condition. Appl Math Model 61:255–279

    Google Scholar 

  69. Ebrahimi F, Farazmandnia N, Kokaba MR, Mahesh V (2019) Vibration analysis of porous magneto-electro-elastically actuated carbon nanotube-reinforced composite sandwich plate based on a refined plate theory. Eng Comput 37:921–936

    Google Scholar 

  70. Ebrahimi F, Hosseini HS (2021) Nonlinear vibration and dynamic instability analysis nanobeams under thermo-magneto-mechanical loads: a parametric excitation study. Eng Comput 37:395–408

    Google Scholar 

  71. Zhou L, Qu F (2023) The magneto-electro-elastic coupling isogeometric analysis method for the static and dynamic analysis of magneto-electro-elastic structures under thermal loading. Compos Struct 315:116984

    Google Scholar 

  72. Zhu S, Yu H, Hao L, Shen Z, Wang J, Guo L (2023) Interaction integral method for thermal fracture of nonhomogeneous magneto-electro-elastic materials. Eur J Mech A/Solids 98:104871

    Google Scholar 

  73. Nan C-W, Liu G, Lin Y (2003) Influence of interfacial bonding on giant magnetoelectric response of multiferroic laminated composites of Tb\(_{1-x}\)Dy\(_x\)Fe\(_2\) and PbZr\(_x\)Ti\(_{1-x}\)O\(_3\). Appl Phys Lett 83:4366

    CAS  Google Scholar 

  74. Wang X, Pan E (2007) Magnetoelectric effects in multiferroic fibrous composite with imperfect interface. Phys Rev B 76:214107

    Google Scholar 

  75. Pan E, Wang X, Wang R (2009) Enhancement of magnetoelectric effect in multiferroic fibrous nanocomposites via size-dependent material properties. Appl Phys Lett 95:181904

    Google Scholar 

  76. Huang Y, Li XF (2010) Shear waves guided by the imperfect interface of two magnetoelectric materials. Ultrasonics 50:750–757

    CAS  PubMed  Google Scholar 

  77. Espinosa-Almeyda Y, López-Realpozo JC, Rodríguez-Ramos R, Bravo-Castillero J, Guinovart-Díaz R, Camacho-Montes H, Sabina FJ (2011) Effects of interface contacts on the magneto electro-elastic coupling for fiber reinforced composites. IntJ Solids Struct 48:1525–1533

    CAS  Google Scholar 

  78. Kuo H-Y (2013) Effective property of multiferroic fibrous composites with imperfect interfaces. Smart Mater Struct 22:105005

    Google Scholar 

  79. Wang YZ (2015) Influences of imperfect interface on effective magnetoelectric properties in multiferroic composites with elliptical fibers. Smart Mater Struct 24:045021

    Google Scholar 

  80. Espinosa-Almeyda Y, Camacho-Montes H, Rodríguez-Ramos R, Guinovart-Díaz R, López-Realpozo JC, Bravo-Castillero J, Sabina FJ (2017) Influence of imperfect interface and fiber distribution on the antiplane effective magneto-electro-elastic properties for fiber reinforced composites. IntD. J Solids Struct 112:155–168

    Google Scholar 

  81. Kuo H-Y, Wu T-J, Pan E (2018) Multilayer multiferroic composites with imperfect interfaces. Smart Mater Struct 27:07532

    Google Scholar 

  82. Jiang J, Zhu J, Chen W (2017) Dispersion curves of magneto-electro-elastic imperfect cylinders filled with fluid. Math Mech Solids 24:195–211

    Google Scholar 

  83. Kuo H-Y, Huang CS, Pan E (2019) Effect of imperfect interfaces on the field response of multilayered magneto-electro-elastic composites under surface loading. Smart Mater Struct 28:115006

    CAS  Google Scholar 

  84. Pang Y, Feng W, Liu J, Zhang C (2019) SH wave propagation in a piezoelectric/piezomagnetic plate with an imperfect magnetoelectroelastic interface. Waves in Random and Complex Media 29:580–594

    Google Scholar 

  85. Amelinckx S (1964) The direct observation of dislocations. Academic Press, New York

    Google Scholar 

  86. Hirth JP, Lothe J (1992) Theory of Dislocations, 2nd edn. Kriger, Melbourne

    Google Scholar 

  87. Sutton AP, Balluffi RW (1995) Interfaces in Crystalline Materials. Oxford University Press, Oxford

    Google Scholar 

  88. Vattré A, Demkowicz MJ (2013) Determining the Burgers vectors and elastic strain energies of interface dislocation arrays using anisotropic elasticity theory. Acta Mater 14:5172–5187

    Google Scholar 

  89. Hirth JP, Pond RC, Hoagland RG, Liu XY, Wang J (2013) Interface defects, reference spaces and the Frank-Bilby equation. Prog Mater Sci 58:749–823

    Google Scholar 

  90. Vattré A (2015) Mechanical interactions between semicoherent heterophase interfaces and free surfaces in crystalline bilayers. Acta Mater 93:46–59

    Google Scholar 

  91. Vattré A (2016) Elastic interactions between interface dislocations and internal stresses in finite-thickness nanolayered materials. Acta Mater 114:184–197

    Google Scholar 

  92. Vattré A, Pan E (2018) Three-dimensional interaction and movements of various dislocations in anisotropic bicrystals with semicoherent interfaces. J Mech Phys Solids 116:185–216

    Google Scholar 

  93. Vattré A, Pan E (2022) Dislocation singularities in layered magneto-electro-elastic plates. Int J Eng Sci 181(103765):2022

    Google Scholar 

  94. Vattré A (2017) Elastic strain relaxation in interfacial dislocation patterns: I. A parametric energy-based framework. J Mech Phys Solids 105:254–282

    Google Scholar 

  95. Vattré A (2017) Elastic strain relaxation in interfacial dislocation patterns: II. From long- and short-range interactions to local reactions. J Mech Phys Solids 105:283–305

    Google Scholar 

  96. Akasheh F, Zbib HM, Hirth JP, Hoagland RG, Misra (2007) Dislocation dynamics analysis of dislocation intersections in nanoscale metallic multilayered composites. J Appl Phys 101:084314

    Google Scholar 

  97. Zbib HM, Overman CT, Akasheh F, Bahr D (2011) Analysis of plastic deformation in nanoscale metallic multilayers with coherent and incoherent interfaces. Int J Plasticity 27:1618–1639

    CAS  Google Scholar 

  98. Salehinia I, Shao S, Wang J, Zbib HM (2014) Plastic deformation of metal/ceramic nanolayered composites. JOM 66:2078–2085

    Google Scholar 

  99. Yang W, Ayoub G, Salehinia I, Mansoor B, Zbib HM (2017) Deformation mechanisms in Ti/TiN multilayer under compressive loading. Acta Mater 122:99–108

    CAS  Google Scholar 

  100. Zbib HM, de la Rubia TD (2002) A multiscale model of plasticity. Int J Plasticity 18:1133–1163

    Google Scholar 

  101. Kapitza P J.E.T.P 11. Collected papers of P. Kapitza. Pergamon Press: Oxford 1941

  102. Benveniste Y (1999) On the decay of end effects in conduction phenomena: a sandwich strip with imperfect interfaces of low or high conductivity. J Appl Phys 86:1273–1279

    CAS  Google Scholar 

  103. Shuttleworth R (1950) The surface tension of solids. Proc R Soc A 63:445–458

    Google Scholar 

  104. Gurtin ME, Murdoch AI (1975) A continuum theory of elastic material surfaces. Arch Ration Mech Anal 57:291–323

    Google Scholar 

  105. Steigmann DJ, Ogden RW (1975) Plane deformations of elastic solids with intrinsic boundary elasticity. Proc R Soc London A 453:853–877

    Google Scholar 

  106. Vattré A, Pan E, Chiaruttini V (2021) Free vibration of fully coupled thermoelastic multilayered composites with imperfect interfaces. Compos, Struct., p 113203

    Google Scholar 

  107. Kumari P, Srivastava R (2021) On reflection and transmission of qP waves in initially stressed viscoelastic triclinic layer between distinct triclinic geomedia with sliding interface. Waves Random Complex Media. https://doi.org/10.1080/17455030.2021.2006358

    Article  Google Scholar 

  108. Duan B, Chai Y, Geng Q, Yang X, Li Y (2023) Study on dynamic characteristics of composite plates under non-uniform gradient temperature along the thickness. J Vib Control. https://doi.org/10.1177/10775463231155711

    Article  Google Scholar 

  109. Chen WQ, Cai JB, Ye GR, Wang YF (2004) Exact three-dimensional solutions of laminated orthotropic piezoelectruc rectangular plates featuring interlaminar bonding imperfections modeled by a general spring layer. Int J Solids Struct 41:5246–5263

    Google Scholar 

  110. Fan H, Sze KY (2001) A micro-mechanics model for imperfect interface in dielectric materials. Mech Mater 33:363–370

    Google Scholar 

  111. Feng X, Zhang L, Hu Z, Zhang H, Gao Y (2022) Guided wave propagation in multilayered two-dimensional quasicrystal plates with imperfect interfaces. Acta Mech Solida Sin 35:694–704

    Google Scholar 

  112. Wang HT, Guo JH, Jiang X, Gao MZ (2022) Bending and vibration of one-dimensional hexagonal quasicrystal layered plates with imperfect interface. Acta Mech 233:4029–4046

    Google Scholar 

  113. Kumari P, Srivastava R (2023) Analysis of quasi waves in orthotropic layer bonded between piezoelectric half-spaces with imperfect and sliding interfaces. J Vib Eng Technol 11(8):1–26

    Google Scholar 

  114. Pan E, Chen W (2015) Static Green’s functions in anisotropic media. Cambridge University Press, Cambridge

    Google Scholar 

  115. Vattré A, Pan E (2021) Thermoelasticity of multilayered plates with imperfect interfaces. Int J Eng Sci 158:103409

    Google Scholar 

  116. Eringen A (1977) Edge dislocation in nonlocal elasticity. Int J Engng Sci 15:177–183

    Google Scholar 

  117. Eringen A, Speziale C, Kim B (1977) Crack-tip problem in non-local elasticity. J Mech Phys Solids 25:339–355

    Google Scholar 

  118. Eringen A (1983) On differential equations of nonlocal elasticity and solutions of screw dislocation and surface waves. J Appl Phys 54:4703–4710

    Google Scholar 

  119. Stroh A (1958) Dislocations and cracks in anisotropic elasticity. Philos Mag 3:625–646

    CAS  Google Scholar 

  120. Stroh A (1962) Steady state problems in anisotropic elasticity. J Math Phys 41:77–103

    Google Scholar 

  121. Vattré A, Pan E (2019) Semicoherent heterophase interfaces with core-spreading dislocation structures in magneto-electro-elastic multilayers under external surface loads. J Mech Phys Solids 124:929–956

    Google Scholar 

Download references

Acknowledgements

The author dedicates this work to the memory of Hussein Zbib and Ladislas Kubin.

Funding

The author declares that he has no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Author information

Authors and Affiliations

  1. Materials and Structures Department, ONERA, Université Paris-Saclay, 29 av. Division Leclerc, 92320, Châtillon, France

    Aurélien Vattré

Authors
  1. Aurélien Vattré
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

Not applicable.

Corresponding author

Correspondence to Aurélien Vattré.

Ethics declarations

Conflict of interest

No conflict of interest exists in the submission of this manuscript. No competing financial interests or personal relationships have appeared to influence the work reported in this paper.

Ethical approval

Not applicable.

Additional information

Handling Editor: M. Grant Norton.

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Vattré, A. Multiphysics modeling and analysis of laminated composites with interfacial imperfections in thermal environments. J Mater Sci 59, 4913–4933 (2024). https://doi.org/10.1007/s10853-023-09205-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10853-023-09205-9

Search

Navigation