Abstract
Density functional theory is used to study the effect of asymmetric in-plane strain on various BiInO3 phases. Structural relaxation is carried out to simulate the growth of coherently strained epitaxial films on (001) oriented orthorhombic perovskite substrates. The results are in particular analyzed with respect to commercially available substrates in order to assess the stabilization of new and fundamentally interesting BiInO3 phases. We find that a pyroxene-like Pcca phase is energetically more favorable than the bulk-like Pna21 structure on standard cubic substrate materials, such as SrTiO3. However, the presence of imaginary phonon modes suggests that this phase is dynamically instable. The bulk-like structure instead is stable over a wide range of lattice in-plane strain, but coherent growth requires substrates with unusually large lattice parameters. We suggest the use of lanthanate substrates in order to produce high-quality thin films of the bulk phase.
Graphical abstract

Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
The stabilization of various BiFeO3 polymorphs has spurred immense research interest in the field of ferroelectric thin film research over the last decade. These polymorphs have vastly different properties that are of great fundamental interest and offer promise for applications. The best studied example is the strain-induced morphotropic phase transition from the bulk-like rhombohedral polymorph toward a highly tetragonal BiFeO3 phase with P4mm symmetry in epitaxial thin films [1]. This transition leads to drastic changes in materials properties including enhanced ferroelectric and piezoelectric properties, a reduction of the optical band gap and a change of magnetic ordering [2, 3].
A rich phase space is common to BiMO3 perovskites, including M = Fe, Al, Ga, Co and In. This behavior is in part related to the well-known tendency of transition metal oxides to accommodate stress by oxygen octahedral rotations with subtle energetic differences between different rotation patterns. The other major contributions are stereochemically active 6s2 lone pairs of Bi3+ ions responsible for the polar distortion. A delicate energy landscape will form for all these materials depending on the orientation of the ferroelectric lattice distortion with respect to their pseudocubic crystal axes. In a recent study, Singh et al. [4] performed a search for local minima in the energy landscape of BiFeO3 using a new generic algorithm based on density functional theory (DFT). They found a staggering number of 15 stable phases within 125 meV per formula unit from the rhombohedral bulk phase, all varying by their characteristics of polar and antipolar distortions. The gap between the tetragonal and rhombohedral polymorph of BiFeO3 is only in the order of 100 meV per formula unit, a value that can be bridged by strain engineering.
BiInO3 (BIO) has recently been synthesized in bulk form and has thus been proven to be at least metastable against decomposition to other oxides [5]. The structure was determined to belong to the Pna21 space group, a non-centrosymmetric subgroup of Pnma. Thus, bulk BIO can be best described as a ferroelectric with polar distorted GdFeO3-type structure, a structure with symmetric oxygen octahedral rotations about all pseudocubic axes that is found quite often among perovskites. No details on magnetic properties have been given, but it stands to reason that In ions remain in their nonmagnetic In3+ states. The bulk phase of BIO is of particular interest, since its symmetry and strong spin–orbit coupling in principle allow for the formation of a persistent spin helix [6].
Although the potential to stabilize new phases is well known for Bi-perovskites, BIO thin films have rarely been studied experimentally and theoretically. We are not aware of any study reporting the successful growth of epitaxial BIO films. In part, this may be related to the large lattice mismatch to commercially available single-crystal perovskite substrates like SrTiO3 or LaAlO3. Additionally, the large polar and antipolar distortions of bulk BIO do not provide a good oxygen connectivity at the interface to standard cubic substrates and epitaxy readily introduces anisotropic in-plane lattice stress. In this paper, we use DFT to study the phase stability of various BIO phases with respect to an orthorhombic in-plane distortion. The purpose of this approach is to identify phase space regions that favor the epitaxial growths of BIO films and are accessible with known substrate materials. Our results suggest that lanthanate single-crystals or buffer layers would provide a perfect template for the growth of bulk-like BIO. On the other hand, a supertetragonal structure, similar to that found in BiFeO3 films under large compressive strain, is expected to be stable on commercially available perovskite substrates with smaller lattice parameters.
Crystal structures and stability
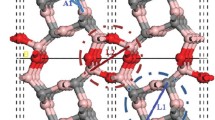
We consider a total of 6 different phases. Structure I is the BIO bulk phase as shown in Fig. 1a. The structure is characterized by large oxygen octahedral rotation about all pseudocubic lattice directions. The octahedral rotation pattern can be described by the a−a−c+ Glazer notation. The polar distortion is along the long c-axis of the unit cell. The orthorhombic lattice parameters experimentally determined by Behlik et al. [5] are a = 5.955 Å, b = 5.602 Å and c = 8.386 Å.
a Representation of the Pna21 bulk structure (structure I). b An epitaxial strain is introduced by modifying the a and b in-plane lattice parameters of the (001) oriented orthorhombic unit cell and relaxing all other lattice degrees of freedom. Rotations and distortions of the oxygen octahedra strongly depend on anisotropic strain, as illustrated for a < b (top) and a > b (bottom)
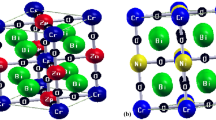
Structures II–VI are shown in Fig. 2. All structures are described in the following:
I: Pna21 symmetry, a−a−c+ octahedral rotation pattern, P along [001]pc
-
BiInO3 bulk structure
II: Pnma symmetry, a−a−c+ octahedral rotation pattern, nonpolar
-
GdFeO3-type structure
III: Pcca symmetry, chains of InO4 polyhedra, nonpolar
-
pyroxene-like structure, ground state of bulk BiGaO3
IV: Cc symmetry, a−a−c0 octahedral rotation pattern, P within (1–10)pc
-
most stable supertetragonal variant of P4mm BiFeO3 polymorph according to Ref. [4]
V: Cm symmetry, a0b+a0 octahedral rotation pattern, P within (100)pc
-
second most stable supertetragonal variant of P4mm BiFeO3 polymorph according to Ref. [4] observed, for example, in BiFe1−xGaxO3 single crystals [7]
VI: R3c symmetry, a−a−a− octahedral rotation pattern, P along [111]pc
-
rhombohedral ground state of BiFeO3
Our selection of phases is motivated by their presence in BiMO3 oxides under biaxial strain or hydrostatic pressure. However, the existence of other low-energy phases that may be stable in thin films cannot be ruled out. In order to further justify our choice, we conduct a universal phase search using the structure prediction code USPEX [8,9,10]. Since a DFT-based run would be computationally too demanding, the USPEX predictions are instead performed with the force field lattice program GULP [11, 12]. The corresponding interatomic potentials are derived from a core–shell model based on Rydberg potentials that has been successfully applied to model BiFeO3 properties before [13]. The potential parameters are then fitted to the 6 structures studied by DFT and their energies (see the supplemental S1 for the full parameter set). The average difference between the free enthalpies of structures calculated with DFT and our interatomic potentials are of the order of 0.4 eV per formula unit. We thus believe that our interatomic potentials are suitable to be used in a general phase search.
Our USPEX run correctly predicts the bulk phase of BiInO3 as the most stable phase and finds a total of 18 phases within 1 eV per formula unit (see S2). We perform a consequential structural relaxation by DFT for all these phases and find that our 6 initially considered experimentally observed phases remain as the lowest in energy.
Dynamical stability
In the next step, all considered structures are studied for their dynamical stability. Phonon dispersion curves are determined by the use of GULP and the interatomic potentials (S3). We confirm the absence of imaginary modes for the bulk phase I as well as structure VI. The presence of an imaginary mode for the nonpolar phase II agrees with a ferroelectric soft mode that results in symmetry lowering toward the polar bulk structure. Our phonon analysis also reveals that the pyroxene-like phase III exhibits a plethora of imaginary modes. Although energetically favorable over a large range of in-plane strain, as will be shown later, it is therefore unlikely that this phase can be stabilized in thin films. Imaginary modes are also present for the IV phase. The phase IV, however, only shows a weakly imaginary mode near the R and S point that might either disappear after a more accurate DFT-based calculation or be suppressed under epitaxial strain. We thus conclude that this supertetragonal phase might potentially be stabilized in thin films.
Epitaxial constraint
In our calculations, the epitaxial constraint is applied onto the a-b plane of the orthorhombic lattice. This scenario corresponds to the growth of BIO films on (001) oriented orthorhombic substrates. Imposing anisotropic strain by varying the a and b parameters independently will drastically affect both oxygen octahedral rotations and distortions, as illustrated in Fig. 1b. This is in contrast to the more commonly studied case of perovskite films grown on cubic substrates. Here, the stress induced by symmetric biaxial in-plane strain is often mainly accommodated by octahedral rotations and the shapes of the oxygen octahedra remain largely unchanged.
It should be noted that the space groups given in the list refer to their bulk structures as experimentally observed. Symmetry lowering due to the epitaxial constraint will occur. For example, the space group of phase VI is commonly found in rhombohedral perovskites with a−a−a− Glazer notation where octahedral rotations occur in equal dimensions about all axis of the pseudocubic unit cell. Heteroepitaxial growth of these materials on cubic substrates will generally induce symmetric biaxial in-plain strain and result in symmetry lowering to monoclinic phases was, for example, shown for BiFeO3 and SrRuO3 [2, 14, 15]. In strained films, in-plane and out-of-plane octahedral rotations are not of the same magnitude anymore and the Glazer notation would be more precisely be described by a−a−c−. In this study, we consider the influence of anisotropic strain imposed by the growth on orthorhombic substrates. In this case, the symmetry of originally rhombohedral materials is lowered even further and structures are triclinic with a−b−c− Glazer notation.
Anisotropic heteroepitaxial strain is expected to modify bond angles, shift cation ions and induce tilts and distortions of oxygen octahedra. Thereby, the use of orthorhombic substrates may allow for stabilization of novel phases and tailoring of film properties beyond that of standard symmetric strain.
Computational details
The DFT calculations were done using the Quantum Espresso code [16, 17]. All calculations were done within the generalized gradient approximation with the Perdew–Burke–Ernzerhof (PBE) functional. The calculations are performed using scalar-relativistic ultrasoft pseudopotentials. Convergence studies have shown using a plane-wave energy cutoff of 800 eV and a 6 × 6 × 6 k-point mesh to be sufficient. Structural optimization is carried out by fixing the in-plane parameters of the unit cell and allowing the out-of-plane lattice parameter and all internal ionic coordinates to fully relax within the specific symmetry of the considered structure. The structural relaxation is continued until all cartesian forces on the ions are less than 4 meV/Å and the total energy difference between structural relaxation iterations is below 1 meV. The ferroelectric polarization is calculated using the berry phase approach as implemented in Quantum Espresso.
Results and discussion
We start with a full structural relaxation of the Pna21 structure in order to confirm consistency with the experimental bulk structure. We find orthorhombic lattice parameters of a = 6.021 Å, b = 5.708 Å and c = 8.454 Å. All calculated lattice parameters are in good agreement with the experimental bulk values (< 1.8% off).
In the next step, the total energy of all considered phases is calculated as a function of the in-plane lattice parameters a and b. The results are plotted as contour plots in Fig. 3. The differences to the bulk Pna21 structure are depicted as insets. The nonpolar variant and the Pnma structure II naturally show very similar characteristics to its polar counterpart. It is higher in energy than the bulk phase within the considered parameter space. This observation confirms that the bulk BIO phase is generally more stable and robust ferroelectricity can be expected.
Total energy of the 6 different structural phases as a function of the a and b in-plane lattice parameters. The values are given with respect to the lowest energy state of the bulk phase. Insets show the energy differences to the bulk structure at identical lattice parameters. The energy minima are marked by red crosses for each phase
Table 1 summarizes the relaxed lattice parameters for all structures as well as their energy minima with respect to the bulk phase. As mentioned above, the phase II is only slightly higher in energy, but the energy landscape is similar to that of the ferroelectric bulk phase. The energy difference between the bulk phase and structure III is small too and the energy landscapes with respect to asymmetric in-plane strain are quite different. The local minima for the pyroxene-like BIO lie at much smaller lattice parameters. The situation appears to be similar to BiFeO3 thin films, where a highly tetragonal polymorph can be stabilized under large epitaxial compressive strain. The pyroxene-like BIO phase would be accessible with standard perovskite substrates. However, our phonon analysis has shown the relaxed structure to be dynamically instable. Experiments and more accurate DFT-based phonon calculations under compressive strain are necessary to clarify this issue.
The phases IV and V are a bit higher in energy. These two phases have similar energy landscapes and properties as they both belong to the subgroup of supertetragonal polymorphs that have drawn much attention in BiFeO3 films. For BIO, the energy differences of supertetragonal phases to the stable bulk structure are larger than in BiFeO3. Therefore, the supertetragonal Cm phase only becomes energetically favorable over the bulk structure at high strain values of > 6%, as compared to about 4.5% for BiFeO3.
Another difference to the BiFeO3 system is that the rhombohedral tilt system (a−a−a−) is energetically quite unfavorable in BIO. The energy difference of structure VI to the bulk structure is larger than 400 meV per formula unit.
In Fig. 4, we present the phase diagram of BIO based on the DFT results. Dynamically unstable phases are discarded. In order to illustrate which single crystals are particularly suitable for the thin film growth of BIO, a number of various well-known substrates are added to the parameter space. We find that while the bulk phase is stable for the largest part of the a–b parameter space, the monoclinic Cm is energetically favored at small lattice parameters. It should be noted that DFT calculations do not take into account the formation of ferroelectric domains. Phase-field modeling of the ferroelectric domain structures would allow for the refinement of the phase diagram as a function of the film thickness.
Calculated phase diagram. The shaded area indicates an uncertainty range of 10 meV/f.u. between the Pna21 and Cm phase. Lattice parameters of a variety of possible substrate materials are included by data points. The dashed yellow and red lines show the parameter space for cubic substrate materials with a/b = 1 and orthorhombic materials with a/b = 1.054, respectively
If the highly polar Cm phase is to be stabilized, standard commercial substrates with small in-plane lattice, such as LaAlO3, are worth considering. However, it is worth mentioning that in the phase space where the Cm phase is favored, this phase is already under a significant misfit strain with respect to its own local minima at apc = 4.016 Å. Experimental realization via thin film growth is likely going to be difficult.
If the bulk phase is desired, substrate materials with large lattice constants (apc, bpc > 4 Å) are needed. Additionally, a large orthorhombic distortion close to that of bulk BIO (a/b = 1.054) would reduce the lattice mismatch further (see red dashed line in Fig. 4) and help eliminating twin formation. Some scandates (MScO3) and lanthanates (LaMO3), with M being a transition metal of the lanthanide series, do fulfill these requirements. They commonly form orthorhombic structures with Pnma symmetry and a−a−c+ octahedral rotation pattern. Thus, they provide a good ideal oxygen octahedra connectivity to the bulk BIO phase. Scandates have become commercially available over the past decade, with PrScO3 being the substrate with the largest lattice parameters. Lanthanates have been notoriously hard to prepare as single crystals due to their high melting points, but successful growth of La(Sc,Lu)O3 has been reported recently [19]. An alternative route might be the use of lanthanate films in form of buffer layers and/or superlattices with BIO. This approach has been shown to be successful for other oxide thin film combinations [20, 21].
The vastly different properties of the phases I and V may allow for a strain control of various functionalities. For example, in Fig. 5 we plot the electronic band gap Eg and the total ferroelectric polarization Ptot as a function of the symmetric in-plane lattice parameter (a = b), mimicking the growth of BIO films on cubic substrates. We find a quite strong dependence of the ferroelectric polarization on strain. This result is in contrast to other Bismuth perovskites, including BiFeO3, that have been shown to be rather insensitive to strain [22]. Our calculated polarization values appear to be unusually small. Kaczkowski [23] noted a huge discrepancy of bulk BIO polarization values in literature ranging from 33 to 166 µC/cm2. The differences can be ascribed to the use of experimental lattice parameters versus full structural relaxation (as done here). This observation further suggests that the value of the spontaneous polarization of BIO is very sensitive to its crystal structure parameters. Similarly, the band gap is significantly reduced under compressive strain. This behavior is known from BiFeO3 films, where the transition from the rhombohedral to the supertetragonal polymorph leads to a lowering of the band gap [2].
Conclusion
Our calculated phase diagram can be seen as a guide to epitaxial growth of BIO thin films. We find that the bulk phase of BIO is stable for large a and b in-plane parameters. MgO single crystals do provide a relatively large in-plane lattice, but the rocksalt structure does not allow for good oxygen connectivity at the interface. Orthorhombic substrates with large pseudocubic lattice parameters are more beneficial as they provide a smaller lattice mismatch and favor good oxygen octahedra connectivity. Thus, the epitaxial growth of bulk-like BIO likely requires the use of nonstandard substrates. We suggest the growth on lanthanate single crystal or buffer layers. On the other hand, epitaxial stabilization of other BIO phases, such as the supertetragonal or pyroxene-like polymorphs, seem experimentally challenging. Approaches beyond simple thin film epitaxy are likely needed. BIO warrants further theoretical and experimental investigation due to strong spin–orbit coupling that could lead to new functionalities.
References
Zeches RJ, Rossell MD, Zhang JX (2009) A strain-driven morphotropic phase boundary in BiFeO3. Science 326:977–980. https://doi.org/10.1126/science.1177046
Sando D, Barthélémy A, Bibes M (2014) BiFeO3 epitaxial thin films and devices: past, present and future. J Phys Condens Matter 26:473201. https://doi.org/10.1088/0953-8984/26/47/473201
Herklotz A, Rus SF, Sohn C (2019) Optical response of BiFeO3 films subjected to uniaxial strain. Phys Rev Mater 3:094410. https://doi.org/10.1103/PhysRevMaterials.3.094410
Singh A, Singh VN, Canadell E (2018) Polymorphism in Bi-based perovskite oxides: a first-principles study. Phys Rev Mater 2:104417. https://doi.org/10.1103/PhysRevMaterials.2.104417
Belik AA, Stefanovich SY, Lazoryak BI, Takayama-Muromachi E (2006) BiInO3: a polar oxide with GdFeO3-type perovskite structure. Chem Mater 18:1964–1968. https://doi.org/10.1021/cm052627s
Tao LL, Tsymbal EY (2018) Persistent spin texture enforced by symmetry. Nat Commun 9:2763–2769. https://doi.org/10.1038/s41467-018-05137-0
Belik AA, Rusakov DA, Furubayashi T, Takayama-Muromachi E (2012) BiGaO3-based perovskites: a large family of polar materials. Chem Mater 24:3056–3064. https://doi.org/10.1021/cm301603v
Oganov AR, Glass CW (2006) Crystal structure prediction using ab initio evolutionary techniques: principles and applications. J Chem Phys 124:244704. https://doi.org/10.1063/1.2210932
Oganov AR, Lyakhov AO, Valle M (2011) How evolutionary crystal structure prediction works—and why. Acc Chem Res 44:227–237. https://doi.org/10.1021/ar1001318
Lyakhov AO, Oganov AR, Stokes HT, Zhu Q (2013) New developments in evolutionary structure prediction algorithm USPEX. Comput Phys Commun 184:1172–1182. https://doi.org/10.1016/j.cpc.2012.12.009
Gale JD, Rohl AL (2003) The general utility lattice program (GULP). Mol Simul 29:291–341. https://doi.org/10.1080/0892702031000104887
Cope ER, Dove MT (2007) Pair distribution functions calculated from interatomic potential models using the general utility lattice program. J Appl Crystallogr 40:589–594
Graf M, Sepliarsky M, Tinte S, Stachiotti MG (2014) Phase transitions and antiferroelectricity in $\mathrm{BiFe}{\mathrm{O}}_{3}$ from atomic-level simulations. Phys Rev B 90:184108. https://doi.org/10.1103/PhysRevB.90.184108
Ziese M, Vrejoiu I, Hesse D (2010) Structural symmetry and magnetocrystalline anisotropy of SrRuO3 films on SrTiO3. Phys Rev B 81:184418. https://doi.org/10.1103/PhysRevB.81.184418
Herklotz A, Kataja M, Nenkov K (2013) Magnetism of the tensile-strain-induced tetragonal state of SrRuO3 films. Phys Rev B 88:144412. https://doi.org/10.1103/PhysRevB.88.144412
Giannozzi P, Baroni S, Bonini N (2009) QUANTUM ESPRESSO: a modular and open-source software project for quantum simulations of materials. J Phys Condens Matter 21:395502. https://doi.org/10.1088/0953-8984/21/39/395502
Giannozzi P, Andreussi O, Brumme T (2017) Advanced capabilities for materials modelling with quantum ESPRESSO. J Phys Condens Matter 29:465901. https://doi.org/10.1088/1361-648x/aa8f79
Vailionis A, Boschker H, Siemons W (2011) Misfit strain accommodation in epitaxial ABO3 perovskites: lattice rotations and lattice modulations. Phys Rev B 83:064101. https://doi.org/10.1103/PhysRevB.83.064101
Uecker R, Bertram R, Bruetzam M (2017) Large-lattice-parameter perovskite single-crystal substrates. J Cryst Growth 457:137–142
Herklotz A, Biegalski MD, Kim H-S (2010) Wide-range strain tunability provided by epitaxial LaAl1-xScxO3 template films. New J Phys 12:113053. https://doi.org/10.1088/1367-2630/12/11/113053
Folkman CM, Das RR, Eom CB (2006) Single domain strain relaxed PrScO3 template on miscut substrates. Appl Phys Lett 89:221904. https://doi.org/10.1063/1.2396920
Ederer C, Spaldin NA (2005) Effect of epitaxial strain on the spontaneous polarization of thin film ferroelectrics. Phys Rev Lett 95:257601. https://doi.org/10.1103/PhysRevLett.95.257601
Kaczkowski J (2019) First-principles study of structural, electronic, ferroelectric, and vibrational properties of BiInO3 under high pressure. J Phys Chem Solids 134:225–237. https://doi.org/10.1016/j.jpcs.2019.06.009
Funding
Open Access funding enabled and organized by Projekt DEAL. A. Herklotz was supported by the federal state of Saxony-Anhalt and the “European Regional Developement Fund” and was funded by the German Research Foundation (DFG)—Grant No. HE8737/1-1. The research in Halle was supported by the Deutsche Forschungsgemeinschaft, SFB 762 Functional Oxide Interfaces (project A9). A. Huon acknowledges the support by the U.S. Department of Energy (DOE), Basic Energy Sciences, Materials Sciences and Engineering Division. F. Herklotz was supported by the Deutsche Forschungsgemeinschaft—Grant No. LA1397/13.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Handling Editor: David Cann.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Herklotz, A., Tippey, K., Huon, A. et al. BiInO3 phases under asymmetric in-plane strain. J Mater Sci 56, 8406–8414 (2021). https://doi.org/10.1007/s10853-021-05807-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10853-021-05807-3