Methods for Gibbs triple junction excess determination: Ti segregation in $\hbox {CoSi}_2$ thin film

Abstract

Methods are presented determining the Gibbs triple junction excess (${\varGamma }^{\text{TJ}}$) of solute segregation in polycrystalline materials from single atom counting in 3D volumes. One method bases on cumulative profile analysis, while two further methods use radial integration of solute atoms. The methods are demonstrated and compared on simulated model volumes which include three grain boundaries joining together at a triple junction with set values for Gibbs grain boundary and triple junction excess. An experimental technique that provides 3D volumes with single atom detection and spatial resolution close to atomic scale is atom probe tomography. An atom probe tomography volume of a $\hbox {CoSi}_2$ thin film that contains three grain boundaries and a triple junction has been acquired. Ti segregation is found qualitatively at the grain boundaries and triple junction. The quantification of the Ti excess at the investigated $\hbox {CoSi}_2$ triple junction reveals for the three introduced methods positive Gibbs triple junction excess values. It demonstrates that there is an excess of Ti at $\hbox {CoSi}_2$ triple junctions and provides opportunities for its quantification.

Appendix: Geometrical considerations

TJ radius ($r_{\text{TJ}}$) and GB overlap determination

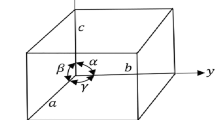
Figure 7 is an visualization of the TJ geometry similar to Fig. 1 with only two GBs that have identical GB width ($d_{\text{GB,1}}=d_{\text{GB,2}}=d_{\text{GB}}$) for simplicity. The projected GB1 appears in a green frame, while GB2 is framed in orange. The center of their junction represents the TJ. The frame of the TJ cylinder projection is drawn as a blue circle. The radius of the TJ cylinder ($r_{\text{TJ}}$) was defined as the radius of the circle that includes all occurring GB overlap at the TJ. The overlapping area is a tetragon and marked in yellow. The illustration shows that $r_{\text{TJ}}$ is thereby defined as the diagonal of the overlapping area of the adjacent GBs in the considered case. The angle of the diagonal of the GB overlap area can be calculated to

$$\begin{aligned} \epsilon &= \frac{\pi -\gamma }{2} \end{aligned}$$

(8)

and with the knowledge of the GB width, the radius of the TJ is

$$\begin{aligned} r_{\text{TJ}} &= \frac{d_{\text{GB}}}{2}\cdot \frac{1}{\cos (\epsilon )}. \end{aligned}$$

(9)

Figure 7

Schema of GB overlap in TJ region for visualization of TJ radius and its calculation as well as calculating the overlap area

Furthermore, the overlapping area of the adjacent GBs is

$$\begin{aligned} S_{12} &= \frac{d_{\text{GB}}}{2}\cdot {\overline{CB}}\nonumber \\ {\overline{CB}} &= \frac{d_{\text{GB}}}{2}\cdot \tan (\epsilon )\nonumber \\ S_{12} &= \left( \frac{d_{\text{GB}}}{2}\right) \cdot \tan (\epsilon ) \end{aligned}$$

(10)

Figure 8

Visualization of single GB fraction in TJ cylinder (no GB overlap). The area of a single GB in the TJ projected along the TJ axis is the sum of the horizontally stripped rectangular area $A_{\text{rect}}$ and the vertically stripped arc area $A_{\text{arc}}$

GB fraction in TJ

The volume fraction of a single GB in the TJ is related to the area of the GB slice in the TJ cylinder projected along the TJ axis (Fig. 8). It is composed of the horizontally dashed rectangular area $A_{\text{rect}}$ and the vertically dashed arc area $A_{\text{arc}}$.

$$\begin{aligned} A_{\text{rect}} &= \sqrt{r_{\text{TJ}}^2-\frac{d_{\text{GB}}^2}{4}}\cdot d_{\text{GB}}\nonumber \\ A_{\text{arc}} &= \pi r_{\text{TJ}}^2\cdot \frac{2 \arcsin \left( \frac{d_{\text{GB}}/2}{r_{\text{TJ}}}\right) }{360^{\circ}}- \frac{A_{\text{rect}}}{2}. \end{aligned}$$

(11)

The so calculated projected GB area requires additional correction when all three GBs are considered in the TJ because of GB overlap (Figs. 1, 7): The half of each of the GB overlap rectangles to the adjacent GBs needs to be subtracted

$$\begin{aligned} A_{\text{GB},i}^{\text{TJ}} &= A_{\text{rect},i}+A_{\text{arc},i}-{\varSigma }_{j\ne i}S_{\text{ij}}/2. \end{aligned}$$

(12)

Knowing this projected GB area in the TJ, the volume fraction is calculated by the ratio to the base area of the TJ cylinder

$$\begin{aligned} f_{\text{GB},i}^{\text{TJ}} &= \frac{A_{\text{GB},i}^{\text{TJ}}}{\pi r_{\text{TJ}}^2}. \end{aligned}$$

(13)

In general, $d_{\text{GB}}$ is not necessarily the same for all three GBs and $r_{\text{TJ}}$ depends on both the GB widths and the dihedral angles of the adjacent GBs. The overlapping areas are than more complex and three cases can be distinguished. In the case that the widths of the GBs are different and $d_{\text{GB},i}>d_{\text{GB,j}}$ and $d_{\text{GB},i}\le |{d_{\text{GB,j}}/\cos (\gamma )}|$ is fulfilled, the equations for $S_{\text{ij}}$ and $r_{\text{TJ}}$ become:

$$\begin{aligned} S_{\text{ij}} &= \frac{d_{\text{GB},i}\cdot d_{\text{GB,j}}}{4}\sin (\gamma )+\frac{d_{\text{GB,j}}^2}{8}\sin (\gamma )\cos (\gamma )\nonumber \\&\quad +\frac{1}{2}\left( \frac{d_{\text{GB},i}}{2}+ \frac{d_{\text{GB,j}}}{2}\cos (\gamma )\right) ^2\arctan (\gamma ) \end{aligned}$$

(14)

$$\begin{aligned} r_{\text{TJ}} &= \sqrt{(d_{\text{GB},i}/2)^2+ (d_{\text{GB},i}/(2\cdot \tan (\gamma ))+d_{\text{GB,j}}/(2\cdot \sin (\gamma )))^2}. \end{aligned}$$

(15)

When $d_{\text{GB},i}<|{d_{\text{GB,j}}/\cos (\gamma )}|$ and $\gamma >\pi /2$, Eqs. 14 and 15 reduce to

$$\begin{aligned} S_{\text{ij}} &= \quad \frac{1}{2}\left( \frac{d_{\text{GB,j}}}{2}\right) ^2\left| \tan (\gamma )\right| \end{aligned}$$

(16)

$$\begin{aligned} r_{\text{TJ}} &= \left| \frac{d_{\text{GB,j}}}{2\cdot \cos (\gamma )}\right| . \end{aligned}$$

(17)