Abstract
Using a combination of extended X-ray absorption fine structure measurements, stochastic quenching (SQ) calculations and Voronoi tessellation analysis, the local atomic environments in thin films of amorphous Sm\(_{x}\)Co\(_{1-x}\) (\(x =\) 0.10, 0.22 and 0.35) are investigated and also compared with crystalline stoichiometric Sm–Co alloys of similar compositions. It is found that the variations in local environment around Co atoms in the amorphous films increase with increasing x and that none of the films exhibit any pronounced short-range order around the Sm atoms. There are, however, signs of clustering of Sm atoms in the SQ-generated simulated amorphous materials. Furthermore, good agreement is observed between experimentally obtained parameters, e.g., interatomic distances and coordination numbers, and those extracted from the simulated alloys. This is a strong indication that SQ provides a powerful route to reliable local structure information for amorphous rare earth–transition metal alloys and that it could be used for designing materials with properties that meet the demands of specific applications.
Similar content being viewed by others
Introduction
Amorphous magnetic materials continue to be of fundamental and technological interest due to a number of appealing properties. They typically have low coercivities and reduced electrical conductivity when compared to their crystalline counterparts, opening up a wide variety of potential applications both in bulk [1] and thin film form [2,3,4], especially since properties can be changed within wide ranges by altering the composition. Additionally, amorphous thin films and heterostructures exhibit highly uniform interfaces [5, 6], which is often a desirable property for applications. Recently, several amorphous Sm–Co thin film and heterostructure systems have been investigated [3, 7,8,9], with particular focus on their magnetic properties. These amorphous Sm–Co alloys retain much of the high magnetic moments that their crystalline counterparts are known for [10], but with a greatly reduced coercivity [3] and high degree of tunability due to a wide range of available compositions. However, while the magnetic properties are relatively straightforward to characterize experimentally, developing a detailed theoretical understanding of their origin is quite challenging. This is due in large part to a limited knowledge of the local atomic structure. Thus, it is of great interest to gain an accurate and detailed model of the atomic positions within these materials. Throughout this paper, we will use the term ‘structure’ in a rather broad sense, to incorporate also arrangements of atoms in amorphous materials.
Computations of amorphous structures can be performed using stochastic quenching (SQ) [11]. The idea behind SQ is to assign any configuration of atoms uniquely to one local minimum of the multidimensional potential energy surface, so that packing and vibrational displacements can be separated. One then employs the single random valley approximation [12], which states that the potential energy surface of a large number of atoms is dominated by degenerate local minima that correspond to maximally amorphous structures. These structures have indistinguishable macroscopic properties. The procedure of quenching a system to its potential energy minima was introduced by Stillinger and Weber [13]. In the SQ approach, rather than quenching from equilibrium molecular dynamics (MD) configurations, one quenches from configurations that are independent of interatomic interactions and are very fast to generate. SQ is therefore a far more computationally efficient alternative to ab initio MD and has been demonstrated to work very well for complex bulk metallic glasses (e.g., Vitreloy 105), monoatomic liquids, amorphous metal carbides and amorphous Gd–TM alloys [11, 14,15,16]. It was thus deemed reasonable to employ SQ also in the current study.
Here, we present a detailed structural analysis of amorphous Sm–Co systems using a combination of SQ and extended X-ray absorption fine structure (EXAFS) measurements. This approach is beneficial in several ways. First, SQ gives a reasonable starting point for the EXAFS analysis, which is a major challenge with any amorphous material. Second, the simulated structures offer far more information about the short-range order (SRO) than EXAFS alone can provide. For example, Voronoi analysis of the simulated structures allows us to compare the local atomic environment in the amorphous systems to that of crystalline materials with similar Sm content. Third, comparison of the experimental EXAFS functions with those derived from the simulated structures enables us to gauge the accuracy of the SQ method in modeling these materials, highlighting strengths and potential limitations.
Methods and materials
This section is divided into one experimental part, describing sample preparation and EXAFS measurements, and one theoretical part with details on calculations and analysis.
Experimental details
The samples were grown by DC magnetron sputtering at room temperature (without substrate cooling) in an UHV chamber with a base pressure below \(3\times 10^{-9}\) Torr. The sputtering gas was Ar (99.999% pure) at a pressure of 2.0 mTorr. Si(100) substrates with a native oxide layer were used, and they were rotated during deposition to ensure homogeneity. First, a 2-nm-thick buffer layer of amorphous AlZr was deposited on the substrate from an Al\(_{0.80}\)Zr\(_{0.20}\) alloy target to avoid crystallization of the following layer [3, 17]. Next, the Sm\(_x\)Co\(_{1-x}\) layers were grown by co-sputtering from Sm and Co targets. Finally, a 3-nm-thick capping layer of amorphous AlZr was deposited to protect the underlying material from oxidation. Two in situ permanent magnets supplied a magnetic field of approximately 0.10 T parallel to the plane of the film during growth, to imprint an anisotropy axis [3, 7]. Actual compositions were determined via Rutherford backscattering spectrometry (RBS) at the Tandem Laboratory, Uppsala, and the thickness and density of each film were determined by X-ray reflectivity (XRR). The three samples in focus here are 51–55 nm thick, with Sm contents \(x=0.10\), \(x=0.22\) and \(x=0.35\), respectively. The growth procedure is described in more detail in a previous paper [3].
EXAFS measurements were taken at the I811 beamline of the MAX II storage ring at MAX-lab, Lund. Absorption spectra at the Co K edge, with all samples cooled to 80 K, were measured in fluorescence mode using an energy-dispersive solid-state detector (Hitachi Vortex 90EX). The number of averaged scans per sample was 8–29, to achieve sufficient signal-to-noise ratios. The spectra were analyzed using the Demeter software package [18].
Analysis of the EXAFS data followed standard procedure [19]. A spline approximation of the background was subtracted in order to isolate the oscillations. Finally, the energies were transformed to k-space using the formula \(k=\sqrt{(2m_{e}/\hbar ^2)\cdot (E-E_{0})}\) to obtain the EXAFS function \(\chi (k)\). As is common practice [19], \(\chi (k)\) was multiplied by a factor of \(k^3\) when plotting, and fitting was done simultaneously, in k space, for weights of k, \(k^2\) and \(k^3\). Fourier transformation over a range from \(k\sim 3.2\;\AA^{-1}\) up to \(k\sim 10.5\)–12.5 \(\AA^{-1}\) resulted in the real space function \(\chi (R)\). The k range limits were taken at points where the EXAFS function crossed zero, with the upper limits chosen to be as high as possible while retaining a reasonable signal-to-noise ratio.
Calculational details and Voronoi analysis
To complement the experimental data, theoretical structures were generated for the same compositions. These computations, based on density functional theory (DFT) [20, 21], were performed using the projector augmented wave [22, 23] method as implemented in the Vienna ab initio simulation package (VASP) [24,25,26]. The exchange correlation energy was calculated using the generalized gradient approximation with the Perdew, Burke and Ernzerhof functional [27] including the valence states 5\(s^2\)5\(p^6\)4\(f^6\)6\(s^2\) for Sm and 3\(d^8\)4\(s^1\) for Co. All calculations were spin polarized. However, spin–orbit coupling was not included, since it was seen to have a negligible effect on the structural properties.
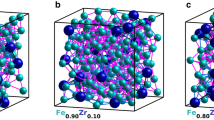
The DFT \(+\,U\) method [28] was applied to Sm with \(U_\mathrm{eff}=7\) eV and \(J=1\) eV. The amorphous structures were generated by means of the SQ method [11, 29], as described in a previous paper [14]. In the initial structures, 200 atoms were randomly distributed both spatially and chemically in a cubic unit cell with a density obtained from fits of XRR measurements, specifically \(\rho =8.61\times 10^{3}\) kg m\(^{-3}\) for Sm\(_{0.10}\)Co\(_{0.90}\), \(\rho =8.51\times 10^{3}\) kg m\(^{-3}\) for Sm\(_{0.22}\)Co\(_{0.78}\) and \(\rho =8.30\times 10^{3}\) kg m\(^{-3}\) for Sm\(_{0.35}\)Co\(_{0.65}\). The atomic positions were then relaxed until the force on every atom was negligible, while keeping the simulation box dimensions constant. The calculations were performed using the \(\varGamma \)k-point. An example of a generated structure is depicted in Fig. 1.
Top: an example of an amorphous Sm\(_{0.10}\)Co\(_{0.90}\) structure obtained with stochastic quenching. Sm atoms are large and dark blue, while Co atoms are small and light blue (radii not to scale). Bottom: Gaussian fit (lines) of the Co–Co (top) and Co–Sm (bottom) partial radial distribution functions (dark blue dots) obtained from SQ simulations of Sm\(_{0.10}\)Co\(_{0.90}\). The thick lines through the simulated data points are the final fits, each obtained by summing five Gaussian functions (thin lines)
To assess the accuracy of the SQ approach for the amorphous Sm–Co systems addressed here, we used the simulated structures to generate starting values for the parameters used in fitting the experimental EXAFS data, with the Artemis software package [18]. To obtain these starting parameters for a specific composition, two partial radial distribution functions (RDFs) were generated: one for Co–Co pairs and one for Co–Sm pairs. Two resulting RDFs for Sm\(_{0.10}\)Co\(_{0.90}\) are shown in Fig. 1. Each RDF was then fit using five Gaussian functions [30, 31], over a range extending up to approximately 7–8 \(\AA\), to ensure that the nearest-neighbor (NN) peak in each RDF was fit as accurately as possible. This is important because the Fourier-transformed experimental EXAFS data only display one clear NN peak for each of the three samples. For each partial RDF, the two Gaussian functions comprising the NN peak then provided the required information: shell positions, coordination numbers and Debye–Waller factors.
The spatial distribution of atoms as well as the internal topology of amorphous systems can be investigated and quantified using the Voronoi tessellation method [32, 33]. A Voronoi polyhedron is a generalization of a Wigner–Seitz cell and consists of the set of points in space which lie closer to a given atom than to any other. The topology of each Voronoi polyhedron is described by its Voronoi index \(\langle n_{3},n_{4},\ldots \rangle \), which lists the number of polygonal faces with increasing number of edges. For example, the Voronoi index \(\langle 0,2,10,2\rangle \) denotes a polyhedron which has 2 quadrilateral faces, 10 pentagonal faces and 2 hexagonal faces. The significance of indices will be included in the discussion below.
Results and discussion
Here, we first account for the analysis of experimental EXAFS data. In the next subsection, the structural information extracted from the combined EXAFS, SQ and Voronoi tessellation approach is discussed further.
EXAFS analysis
Although four shells were initially obtained for each composition (two from each partial RDF), it was found that only two shells were needed to fit the nearest-neighbor (NN) peak in each experimental EXAFS function. Furthermore, for Sm\(_{0.10}\)Co\(_{0.90}\) (\(x=0.10\)), the experimental peak was best fit using two Co shells (i.e., those obtained from the Co–Co partial RDF), while the other two compositions were fit using one Co shell and one Sm shell (i.e., the lowest-R shell from the Co–Co and Co–Sm partial RDFs, respectively).
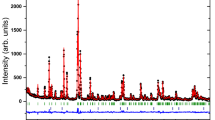
For \(x=0.10\), the ratio between the two Co shell positions was held constant, whereas for \(x=0.22\) and \(x=0.35\) the Co and Sm shell positions were decoupled during fitting. Additional fitting parameters were the amplitude \(S_{0}^{2}\), the absorption edge energy \(E_{0}\) and a separate Debye–Waller factor \(\sigma ^2\) for each shell. The resulting fits in k space and in R space are shown in Figs. 2 and 3, respectively.
EXAFS and Artemis fit in k space (\(k^3\) weighted) for the Co K edge for all three compositions. Sm\(_{0.10}\)Co\(_{0.90}\) was fit using two Co shells, while Sm\(_{0.22}\)Co\(_{0.78}\) and Sm\(_{0.35}\)Co\(_{0.65}\) were each fit using one Co shell and one Sm shell. Parameters are given in Table 1
Magnitude of the EXAFS and Artemis fit in R space for the Co K edge for all three compositions. Sm\(_{0.10}\)Co\(_{0.90}\) was fit using two Co shells, while Sm\(_{0.22}\)Co\(_{0.78}\) and Sm\(_{0.35}\)Co\(_{0.65}\) were each fit using one Co shell and one Sm shell. Parameters are given in Table 1
A comparison of the parameters obtained from both the RDFs and the fits of the experimental data can be found in Table 1. The coordination numbers (CNs) were fit indirectly through the amplitude \(S_{0}^{2}\), by multiplying the input RDF coordination number by the ratio \(S_{0}^{2}/S_{0,\mathrm {Co}}^{2}\), where \(S_{0,\mathrm {Co}}^{2}\) is the amplitude from a fit of a crystalline Co reference spectrum.
As shown in the figures and Table 1, the fits which originate from the SQ simulations closely match the experimental EXAFS data, but there are some key differences. Perhaps most obvious is that the RDFs derived from the simulations required four Gaussians in total to fit the separate Co–Co and Co–Sm NN peaks, whereas the experimental data only required two shells as mentioned above. It is worth noting that three shells have been used by others in experimental studies on TbFe [34]. Furthermore, the experimental peak is dominated by the Co–Co shell for all samples, even when the Sm content is \(x=0.35\). This is perhaps not surprising given the fact that the expected Co–Sm NN distance lies at the edge of the fitting range, which also accounts for the large uncertainties obtained for the Sm \(\sigma ^2\) and R values. If only the tail of the Co–Sm shell overlaps with the main peak in the EXAFS spectrum, the shell properties can vary significantly without having a large effect on the fit. That being said, the exclusion of the nearest Sm shell (at 2.97(1) \(\AA\) with a CN of 1.0(4) \(\AA\)) from the fit for Sm\(_{0.10}\)Co\(_{0.90}\) may account for the discrepancy between fit and RDF for CN\(_{1}\) and CN\(_{2}\) (Table 1).
Several conclusions can be drawn from the results of the fits. First of all, the interatomic distances (\(R_{1}\)) are the same, within the uncertainties, as in the simulated structures, except for the Sm\(_{0.22}\)Co\(_{0.78}\) Co–Co distance. Since the RDF \(R_{1}\) values for Sm\(_{0.22}\)Co\(_{0.78}\) and Sm\(_{0.35}\)Co\(_{0.65}\) correspond to the lower-R shell out of the two Gaussians used to fit the NN peaks, it can be expected that they are lower than the actual values. The \(\sigma ^2\) values are also affected by the choice of shells. The coordination numbers agree within uncertainty between simulation and experiment. Adding CN\(_{1}\) and CN\(_{2}\) gives a measure of the total neighbor count in both shells.
Thus, it is seen that the SQ method generates parameters that are comparable to the results of fits of experimental EXAFS data. The high computational efficiency of SQ makes the combined EXAFS-SQ approach a powerful method for investigating the local structure in amorphous Sm–Co. However, while the R values generally agree with experiment, the \(\sigma ^2\) values derived from the RDFs are mostly larger than the values obtained from the experimental fits, with consistently larger uncertainties. This indicates a higher degree of disorder in the simulated structures.
Structure analysis
Based on the analysis of interatomic distances and partial coordination numbers obtained from Voronoi tessellation, as will be described below, we draw a number of conclusions. The Sm atoms have less SRO around them than the Co atoms, and the disorder increases with increasing Sm content. However, even in the \(x=0.10\) amorphous alloy, the Sm atoms in the simulated structures tend to have more Sm neighbors than in the corresponding crystalline materials. For the Co atoms, which for \(x=0.10\) have a considerable population of local environments similar to those in crystalline phases, the disorder also increases with increasing x. This will now be elaborated.
The agreement between the simulated and measured EXAFS functions confirms that the amorphous structures generated with SQ are a realistic representation of the actual samples. This allows us to use the simulations like a microscope to further study the atomic structure, which is of great value due to the shortage of experimental methods for investigating individual atomic positions in amorphous materials. To analyze the distances between the two types of atomic constituents, Sm and Co, we start by looking at the RDFs from SQ. As shown in Fig. 4, some amount of SRO definitely exists up to \(\sim 6\;\AA\) for Sm–Sm and Sm–Co pairs, and up to \(\sim 5\;\AA\) for Co–Co pairs.
In Table 2, we compare the average NN distances (taken over the first peak in the RDF with a cutoff at the first minimum) of the simulated amorphous structures to crystalline Sm–Co compounds with similar Sm content. The NN distance in atomic pair A–B is here defined as the distance to the nearest B atom from an A atom. For the Co–Co spacing, there is a slight decrease in nearest-neighbor distance \(d_\mathrm{am}\) as the Sm content x increases. This trend is not seen in the crystalline materials, where the Co–Co spacing in SmCo\(_{2}\) (cubic) is the largest. The Sm–Co NN distance in the amorphous materials is independent of x within the uncertainties and larger than in the crystalline counterparts. Finally, the Sm–Sm spacing in the amorphous materials is significantly larger than in the corresponding crystalline materials, with the exception of \(x=0.10\). It should be noted that there are no Sm atoms which are adjacent to other Sm atoms in crystalline Sm\(_2\)Co\(_{17}\). These data provide the first hint that the local structure around Co atoms in the amorphous materials bears more similarity to that of the crystalline materials, compared with the local structure around Sm atoms.
Occurrence of different Voronoi polyhedra of Co (blue, left) and Sm atoms (orange, right) in amorphous Sm\(_{0.10}\)Co\(_{0.90}\) (a, b), Sm\(_{0.22}\)Co\(_{0.78}\) (c, d) and Sm\(_{0.35}\)Co\(_{0.65}\) (e, f). Only polyhedra with a population of more than 2% for Co or more than 1.25% for Sm are displayed and grouped according to the sum of indices (the ‘coordination number’, CN, as discussed in the text). Darker colors indicate polyhedra that are also found in crystalline compounds with similar Sm content. Note that the fraction scales are different for Co and Sm central atoms. The accumulated fractions of indices with populations below cutoff (i.e. not shown) are a 42.8%, c 34.4%, e 33.8% for Co, and b 71.5%, d 88.6%, f 90.1% for Sm
To further analyze the internal topology and atomic distributions, we performed Voronoi tessellation analysis, first with focus on the prevalence of specific Voronoi indices within the materials. In Fig. 5, we show the occurrence of Voronoi polyhedra around Co and Sm central atoms for all three compositions. For Co, only polyhedra which comprise more than 2% of the total population are displayed, while for Sm atoms this cutoff is 1.25%. Indices which also occur in the corresponding crystalline phases are indicated by darker color. Additionally, in Table 3 we list all of the Voronoi indices which exist in the crystalline phases, along with the most common index in the corresponding amorphous phase. For each index, its prevalence within both material types is included for comparison.
The number of occurring indices and their respective frequency within the population directly give an indication about the degree of SRO. Many different indices and a small maximum relative population are clear signs of a lower degree of local order, when compared with fewer indices with large populations. There are several clear trends. First, amorphous Sm\(_{0.10}\)Co\(_{0.90}\) appears to retain a significant amount of a local order similar to that found in crystalline Sm\(_2\)Co\(_{17}\), at least around Co atoms. As the Sm content x increases, however, the degree to which the crystalline SRO is retained decreases considerably. The addition of Sm to Co is generally understood to induce an amorphous structure (assuming a high quenching rate during sample fabrication) and that effect is quantified here. Second, virtually all SRO around Sm atoms is lost in the amorphous phases, even for low Sm concentrations. This is made especially clear by the fact that in all three amorphous compositions, the most common Voronoi indices only account for 2–3% of their respective populations.
Distribution of the theoretical average coordination numbers in amorphous Sm\(_{0.10}\)Co\(_{0.90}\) (circles), Sm\(_{0.22}\)Co\(_{0.78}\) (squares) and Sm\(_{0.35}\)Co\(_{0.65}\) (triangles), along with splines (solid lines). Here, \(n_\mathrm{Sm}\) (\(n_\mathrm{Co}\)) denotes the fraction of Sm (Co) atoms surrounded by \(n_\mathrm{NN}\) Sm or Co nearest neighbors. Vertical lines mark the coordination numbers for crystalline Sm\(_{2}\)Co\(_{17}\) (dotted), Sm\(_{2}\)Co\(_{7}\) (dashed) and SmCo\(_{2}\) (dash dotted). Note the different scales on the vertical axes
Since each face of a Voronoi polyhedron corresponds to a neighboring atom, we may refer here to the sum of the Voronoi indices as the coordination number. However, it should be noted that this value cannot be directly compared to the traditional coordination number as defined for crystalline systems, because non-nearest-neighbor atoms can still correspond to faces on the Voronoi polyhedron. For example, in the case of a bcc lattice, each atom has 8 nearest neighbors, but a Voronoi index of \(\langle 0,6,0,8\rangle \).
In Fig. 6, we show the distribution of the theoretical average coordination numbers, i.e. sums of Voronoi indices for the simulated structures, in the amorphous phases. For comparison, the partial coordination numbers from the corresponding crystalline materials have been included in the figure as well. The distributions appear to be approximately Gaussian. Note that the CNs in Fig. 6 are not the same as CN\(_{1}\) or CN\(_{2}\) from Table 1. As one would expect, the average Sm–Sm and Co–Sm coordination numbers increase with increasing Sm content x, whereas the average Sm–Co and Co–Co coordination numbers decrease correspondingly as the amount of Co decreases. Lastly, one can see that the Sm–Co, Co–Sm and Co–Co average coordination numbers in the amorphous phases are comparable to those in the crystalline compounds, while Sm–Sm average coordination numbers are higher in the amorphous phases for all x values. This once again illustrates the differences between Co and Sm in terms of how many of the crystalline local order exists in the amorphous phases. It also indicates that the Sm atoms are not evenly distributed within the material, but seem to be forming disordered clusters within the simulated structure. This is actually visible in, e.g., Fig. 1. Here, we must emphasize that an experimental verification of Sm clustering in the real amorphous samples would require EXAFS measurements on a Sm absorption edge.
Conclusions
EXAFS and stochastic quenching (SQ) modeling have been combined to create an investigative tool that is more powerful than its individual parts and that has been used to gain deep insight into the local structure of amorphous Sm\(_{x}\)Co\(_{1-x}\), with \(x=0.10\), \(x=0.22\) and \(x=0.35\). While SQ could have been used on its own to simulate the atomic-scale structures, one could not be certain of the method’s accuracy (nor that of any subsequent analysis of the simulated structures) without using EXAFS as a benchmark. Likewise, analyzing EXAFS data requires a reasonable starting arrangement of the atoms, which poses an enormous challenge for amorphous materials. Thus, the combination provides an improved route for probing the local atomic structure in such cases and therefore also for disclosing the origins of properties of various specific alloys. We therefore see a useful way of designing material structures that could meet the demands of specific applications. For future work, direction-dependent EXAFS [34, 38] would make it possible to extend the investigations also to anisotropic material properties.
Good agreement is demonstrated between theory and experiment, particularly in terms of interatomic distances and coordination numbers. From Voronoi analysis of the simulated structures, it is found that some of the Co atoms maintain a local environment similar to that found in the crystalline phases and that this partial order drops as the Sm concentration increases. This trend is not, however, found for the Sm atoms, for which it can be concluded that the amorphous phases provide significantly different local environments than the crystalline counterparts. Comparisons of the amorphous and crystalline interatomic spacing and coordination number distributions reinforce this conclusion. In particular, Sm atoms in the amorphous alloys tend to have more Sm neighbors, also in Sm\(_{0.10}\)Co\(_{0.90}\), at least in the simulations. The presence or absence of Sm clusters in real samples will have to be explored in measurements that are beyond the scope of the present investigation.
References
McHenry M, Willard M, Laughlin D (1999) Amorphous and nanocrystalline materials for applications as soft magnets. Prog Mater Sci 44(4):291–433
Cid R, Rodríguez-Rodríguez G, Álvarez-Prado LM, Díaz J, Alameda JM (2007) Temperature dependence of the anisotropy of amorphous NdCo\(_{5}\) thin films. J Mag Mag Mater 316:e446–e449
Magnus F, Moubah R, Roos A, Kruk A, Kapaklis V, Hase T, Hjörvarsson B, Andersson G (2013) Tunable giant magnetic anisotropy in amorphous SmCo thin films. Appl Phys Lett 102:162402
Soltani ML (2007) Structural, compositional and annealing effects on magnetic properties in R\(_{1-x}\)Co\(_{x}\) (R = Er, Tb, Sm) amorphous thin film alloys. J Non-Cryst Solids 353:2074–2078
Choi CM, Song JO, Lee SR (2005) Thermal stability of magnetic tunnel junctions with new amorphous ZrAl-alloy films as the under and capping layers. IEEE Trans Magn 41(10):2667–2669
Muscas G, Brucas R, Jönsson PE (2018) Bringing nanomagnetism to the mesoscale with artificial amorphous structures. PRB 97:174409
Magnus F, Moubah R, Kapaklis V, Andersson G, Hjörvarsson B (2014) Magnetostrictive properties of amorphous SmCo thin films with imprinted anisotropy. Phys Rev B 89:134414
Procter RA, Magnus F, Andersson G, Hjörvarsson CSHB, Hase TPA (2015) Magnetic leverage effects in amorphous SmCo/CoAlZr heterostructures. Appl Phys Lett 107:062403
Walther A, Marcoux C, Desloges B, Grechishkin R, Givord D, Dempsey NM (2009) Micro-patterning of NdFeB and SmCo magnet films for integration into micro-electro-mechanical-systems. J Magn Magn Mater 321(6):590–594
Kumar K (1988) RETM\(_{5}\) and RE\(_{2}\)TM\(_{17}\) permanent magnets development. J Appl Phys 63(6):R13–R57
Holmström E, Bock N, Peery T, Chisolm E, Lizárraga R, Lorenzi-Venneri GD, Wallace D (2010) Structure discovery for metallic glasses using stochastic quenching. Phys Rev B 82:024203
Wallace DC (1997) Statistical mechanics of monatomic liquids. Phys Rev E 56:4179
Stillinger FH, Weber TA (1984) Packing structures and transitions in liquids and solids. Science 225:983–989
Kádas K, Andersson M, Holmström E, Wende H, Karis O, Urbonaite S, Butorin SM, Nikitenko S, Kvashnina KO, Jansson U, Eriksson O (2012) Structural properties of amorphous metal carbides; theory and experiment. Acta Mater 60:4720–4728
Chimata R, Isaeva L, Kádas K, Bergman A, Sanyal B, Mentink JH, Katsnelson MI, Rasing T, Kirilyuk A, Kimel A, Eriksson O, Pereiro M (2015) All-thermal switching of amorphous Gd–Fe alloys: analysis of structural properties and magnetization dynamics. Phys Rev B 92:094411
Lizárraga R (2016) Structural and magnetic properties of the Gd-based bulk metallic glasses GdFe\(_{2}\), GdCo\(_{2}\), and GdNi\(_{2}\) from first principles. Phys Rev B 94:174201
Korelis PT, Liebig A, Björck M, Hjörvarsson B, Lidbaum H, Leifer K, Wildes AR (2010) Highly amorphous Fe\(_{90}\)Zr\(_{10}\) thin films, and the influence of crystallites on the magnetism. Thin Solid Films 519(1):404–409
Ravel B, Newville M (2005) ATHENA, ARTEMIS, HEPHAESTUS: data analysis for X-ray absorption spectroscopy using IFEFFIT. J Synchrotron Radiat 12:537–541
Bunker G (2010) Introduction to XAFS: a practical guide to X-ray absorption fine structure spectroscopy. Cambridge University Press, Cambridge
Hohenberg P, Kohn W (1964) Inhomogeneous electron gas. Phys Rev 136:B864
Kohn W, Sham L (1965) Self-consistent equations including exchange and correlation effects. Phys Rev 140:A1133
Blöchl PE (1994) Projector augmented-wave method. Phys Rev B 50(24):17953
Kresse G, Joubert D (1999) From ultrasoft pseudopotentials to the projector augmented-wave method. Phys Rev B 59:1758
Kresse G, Hafner J (1993) Ab initio molecular dynamics for liquid metals. Phys Rev B 47:558
Kresse G, Furthmüller J (1996) Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput Math Sci 6:15–50
Kresse G, Furthmüller J (1996) Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys Rev B 54:11169
Perdew JP, Burke K, Ernzerhof M (1996) Generalized gradient approximation made simple. Phys Rev Lett 77:3865
Dudarev SL, Botton GA, Savrasov SY, Humphreys CJ, Sutton AP (1998) Electron-energy-loss spectra and the structural stability of nickel oxide: an LSDA + U study. Phys Rev B 57:1505
Holmström E, Bock N, Peery TB, Lizárraga R, Lorenzi-Venneri GD, Chisolm ED, Wallace DC (2009) Ab initio method for locating characteristic potential-energy minima of liquids. Phys Rev E 80:051111
Stern EA (1974) Theory of the extended X-ray-absorption fine structure. Phys Rev B 10:3027
Balerna A, Bernieri E, Burattini E, Kuzmin A, Lusis A, Purans J, Cikmach P (1991) EXAFS studies of MeO\(_{3-x}\) (Me = W, Mo, Re, Ir) crystalline and amorphous oxides. Nucl Instrum Methods Phys Res Sect A 308:234
Finney JL (1970) Random packing and the structure of simple liquids. Proc R Soc A 319:479–493
Ma E (2015) Tuning order in disorder. Nat Mater 14:547
Harris VG, Aylesworth KD, Das BN, Elam WT, Koon NC (1992) Structural origins of magnetic anisotropy in sputtered amorphous Tb–Fe films. Phys Rev Lett 69(13):1939
Buschow KHJ, Goot ASVD (1968) Intermetallic compounds in the system samarium-cobalt. J Less Common Met 14(3):323–328
Buschow KHJ (1966) The crystal structure of the rare-earth compounds of the form R\(_{2}\)Ni\(_{17}\), R\(_{2}\)Co\(_{17}\), and R\(_{2}\)Fe\(_{17}\). J Less Common Met 11(3):204–208
Khan Y (1974) A contribution to the Sm–Co phase diagram. Acta Cryst B 30:861–864
Ruffoni M, Pettifer R, Pascarelli S, Trapananti A, Mathon O (2007) Probing atomic displacements with thermal differential EXAFS. J Synchrotron Rad 14:421–425
Acknowledgements
Open access funding provided by Uppsala University. The authors would like to thank Dimitri Arvantis for sharing his knowledge and expertise in the EXAFS analysis process, as well as Stefan Carlson for his assistance during the EXAFS measurements at MAX-lab, Lund. The computations were performed on resources provided by the Swedish National Infrastructure for Computing (SNIC) at the National Supercomputer Center (NSC), Linköping University, the PDC Centre for High Performance Computing (PDC-HPC), KTH, and the High Performance Computing Center North (HPC2N), Umeå University. Financial support from the Swedish Research Council (G.A. Contract No. 2013-03927; P.J. Contract No. 2014-05951), Swedish Energy Agency (STEM), the Foundation for Strategic Research (SSF), eSSENCE, and STandUP is acknowledged. F.M. acknowledges funding from the Icelandic Research Fund (Grant No. 174271-053).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflicts of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
George, S., Kádas, K., Jönsson, P.E. et al. Local structure in amorphous Sm\(_x\)Co\(_{1-x}\): a combined experimental and theoretical study. J Mater Sci 55, 12488–12498 (2020). https://doi.org/10.1007/s10853-020-04848-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10853-020-04848-4