Superelastic behavior of a metamagnetic Ni–Mn–Sn single crystal

P. Czaja; R. Chulist; T. Tokarski; T. Czeppe; Y. I. Chumlyakov; E. Cesari

doi:10.1007/s10853-018-2289-1

Journal of Materials Science

pp 1–13 | Cite as

Superelastic behavior of a metamagnetic Ni–Mn–Sn single crystal

Authors
Authors and affiliations

P. CzajaEmail author
R. Chulist
T. Tokarski
T. Czeppe
Y. I. Chumlyakov
E. Cesari

Open Access

Metals

First Online: 17 April 2018

Received: 21 December 2017

Accepted: 02 April 2018

2 Downloads

Abstract

A single-crystalline specimen with the composition of Ni_49.5Mn_38.4Sn_12.2 shows a 4.9% recoverable transformation strain upon compressive loading. The critical compressive stress increases with temperature at the step of 5.6 MPa/K, whereas upon cycling it decreases by 18.1 MPa/cycle. The microstructure of the specimen undergoes considerable refinement upon superplastic training; however, it is only able to sustain a limited number of cycles (≤ 5). Martensite training, resulting in a single-variant microstructure, has a profound influence on the austenite start transformation temperature (ΔT = 29 K), resulting partially from the dissipation of the elastic strain energy. The Ni-Mn-Sn system is an interesting candidate for multiferroic applications given its mechano-magnetic properties and a huge value of the martensitic transformation entropy change (~ 50 J/kg K).

Download article PDF

Introduction

The specific volume and vibrational entropy changes (ΔS^transf.) accompanying the first-order, thermoelastic martensitic phase transformation (MPT) in Ni-Mn-based metamagnetic shape memory alloys have recently encouraged much interest, owing to their additional coupling with the volume-dependent spin-exchange interactions [1, 2]. The ramifications of the coupling for such systems being so that a magnetic field (μ₀·H) is able to suppress the MPT at a given compositional range assumed that the exerted magneto-stress level exceeds the transformation hysteresis (ΔT_hyst. = A_f − M_s); that is, $ A_{\text{f}}^{{\mu_{0} \cdot H}} < M_{\text{s}} $, where the A_f and M_s denote austenite finish and martensite start characteristic temperatures, respectively [3]. The shift of the latter under magnetic field can be satisfactorily predicted according to the classical Clausius–Clapeyron relationship, introducing further means for understanding and control of such a behavior [4]. A large magneto-stress combined with a reduced ΔT_hyst. provide for decremented μ₀·ΔH, critical to instigate a reverse MPT, when the field is applied to a weakly magnetic martensite state. This in turn is of paramount significance in the view of actuation, sensing, etc., applications and can be well tuned through composition and microstructure engineering [5, 6]. Concomitantly in thermodynamic terms, the magneto-elastic coupling can produce huge magnetic entropy (ΔS^mag). increase, when a magnetic field is applied isothermally, and a decrease in temperature (cooling), when the field is applied adiabatically, leading overall to a considerable inverse magneto-caloric effect, e.g., 18 J/kg K under μ₀·ΔH = 5 T in polycrystalline Ni_0.50Mn_0.50−xSn_x (0.13 ≤ x ≤ 50) alloys [7]. What’s more the induction of a large ΔS is not solely limited to the magnetic field, but due to the intrinsic nature of thermoelastic MPT it can be also assisted with a mechanical force offering substantial mechano-caloric response, e.g., elastocaloric [8], which is an incentive for solid-state refrigeration [9]. In fact, more recently a large elastocaloric effect (ECE) on the order of ΔT_ad. = 4 K at a relatively moderate ~ 1.3% transformation strain (ε^transf.) has been reported upon unloading the Ni₄₅Mn₄₄Sn₁₁ [10] and Ni₄₈Mn₃₅In₁₇ (ε^transf. ~ 1.4%) [11] polycrystalline alloys. It has been superseded shortly after by the Ni₄₄Mn₄₁Sn₁₁Cu₄ alloy showing ΔT_ad. = 8 K at the similar ε^transf. [12] and earlier by the single-crystalline Ni₅₀Fe₁₉Ga₂₇Co₄ yielding ΔT_ad. ~ 10 K (ε^transf. ~ 10%) [13]. A notable 4% recoverable ε^transf. has been further found in Mn₄₉Ni₃₉Sn₉ highlighting the Ni-Mn-Sn system among other polycrystalline Ni-Mn-based alloys [14], also partially thanks to a peculiar inverse ECE in Ni₅₀Mn₄₀Sn₁₀ ribbons [15]. In the previous communications, the authors reported the 7.9% twinning strain upon uniaxial compression, applied in the martensite state, along the 〈001〉 direction in the Ni_49.5Mn_38.4Sn_12.2 single crystal [16]. At room temperature, the specimen presented a complex hierarchical, self-accommodated microstructure, refinable with the aid of the training process [17]. The austenite Curie temperature ($ T_{\text{C}}^{\text{A}} $) in the specimen was found at 311 K, whereas its M_s = 348 K while the M_f = 305 K, what indicates that the fraction of austenite undergoing the MPT in the paramagnetic state to the weakly magnetic/paramagnetic martensite in this alloy is around $ f_{{{\text{aust}} .}}^{{{\text{para}} .}} = \left( {M_{\text{s}} - T_{\text{C}}^{\text{A}} )/(M_{\text{s}} - M_{\text{f}} } \right) $ ≥ 86% what then likely benefits the overall ΔS^transf. and thus ΔT_ad., given the opposing contributions to the ΔS^transf. arising from the vibrational and magnetic terms ΔS^transf = ΔS^vib.(< 0) + ΔS^mag.(> 0) [18]. The MPT between paramagnetic austenite and paramagnetic/weak magnetic martensite simultaneously attenuates the magneto-volume-related effects what may have a positive impact on the cycle life time improvement of the Ni_49.5Mn_38.4Sn_12.2 alloy [2]. Henceforth, the present contribution investigates a pseudoelastic strain in the Ni_49.5Mn_38.4Sn_12.2 single crystal and discusses the influence of microstructure refinement on the reduction of the critical compressive stress ($ \sigma_{{{\text{cr}} .}}^{\text{transf}} $), the ΔT_hyst. as well as on the evolution of characteristic MPT temperatures. Overall, the contribution offers an interesting insight into the thermo-mechanics of a Ni-Mn-Sn single crystal inasmuch as it promotes the feasibility of applying a combined thermo-magneto-mechanical stimuli for harnessing an enhanced multiferroic response.

Experimental

The single-crystalline specimen with the nominal composition of Ni₅₀Mn_37.5Sn_12.5 was grown by the Bridgman method. It was further annealed until it finally equilibrated with the Ni_49.5Mn_38.4Sn_12.2 (at.%) composition. For more details see [16]. Two rectangular prisms with 2.32 × 2.58 × 3.67 mm and 2.36 × 2.53 × 3.7 mm dimensions were wire-cut from the master ingot, and they were found to deviate by 9° from the ideal [001] orientation relative to the cubic L2₁ austenite phase. Mechanical testing was performed with an Instron machine at the temperature range between 343 K and 373 K and with a strain rate (SR) of 3.7 × 10⁻⁴ s⁻¹. The resulting microstructure prior to testing and following straining has been inspected with a FEI-ESEM XL-30 scanning electron microscope (SEM) and with a Tecnai G2 (200 kV) transmission electron microscope (TEM). Thin foils for TEM were prepared by standard electro-polishing [16] and by focused ion beam (FIB) employing FEI-FIB Quanta 3D. Thermal effects at 10 K/min heating/cooling rate were investigated by differential scanning calorimetry (DSC) within the 173–423 K temperature range with the aid of a DSC Q1000 TA instrument.

Results and discussion

The pseudoelastic behavior of the Ni_49.5Mn_38.4Sn_12.2 single crystal is shown in Fig. 1. The compressive test was performed at 363 K, and prior to compression the specimen was heated up to 473 K in order to ensure that at the test temperature (T_test) M_s< T_test and the specimen is completely retransformed to the austenite state. The sample was loaded until the compressive stress (σ) spiked up, however below the yield stress, and then, it was released. The specimen showed a typical superelastic response (Fig. 1). Initially, with increasing stress the austenite yields elastically, before it begins to transform to martensite at the strain range where the stress levels off. The critical transformation stress $ \left( {\sigma_{{M_{\text{s}} }} } \right) $, which triggers the MPT, is marked in Fig. 1, and it is estimated by the intersecting tangents method to be equal to 258 MPa. At the plateau region, the austenite continues to transform to martensite (4O-modulated structure [16]) and simultaneously the formed martensite undergoes detwinning process. A sudden drop of σ at circa 6% compressive strain is characteristic for the detwinning process and may be ascribed to martensite structure refinement just as observed in response to the mechanical training [16]. At about 6.7% strain following yet another, however less apparent fall in σ indicating again the detwinning process, the stress begins to step up marking the compression range where the martensite starts simultaneously to deform elastically. The compressive stress was elevated up to 600 MPa, and then, the specimen was gradually unloaded. Upon unloading, the specimen relaxed to the initial state going through the elastic relaxation of martensite first, which followed suite by retransformation to austenite when σ decreased to 124 MPa ($ \sigma_{{A_{\text{f}} }} $), marked in Fig. 1. The resulting transformation strain approximated from the plateau has the value of 4.9%, which approaches the 77% of the theoretical transformation strain $ \varepsilon_{{{\text{transf}} .}}^{{{\text{theor}} .}} = \frac{{\left( {a_{{{\text{aust}} .}} - c_{{{\text{mart}} .}} } \right)}}{{a_{{{\text{aust}} .}} }} \times \cos \alpha = 6.4\% $, computed based on the lattice parameters of the martensite phase ($ c_{{{\text{mart}} .}} $) and austenite phase ($ a_{{{\text{aust}} .}} $) and the deviation angle α from the ideal [001] orientation of the tested single-crystalline specimen [17, 19]. The stress hysteresis is circa 110 MPa. When concluding the experiment, there was no residual strain left when the load was removed entirely, confirming full reversibility of the specimen at the test temperature of 363 K.

Figure 1
Isothermal-compressive stress-compressive strain curve upon loading and unloading the Ni_49.5Mn_38.4Sn_12.2 single crystal at the strain rate SR = 3.7 × 10⁻⁴ s⁻¹

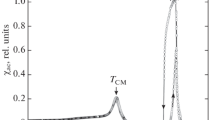
In the forthcoming section, the influence of temperature on the stress–strain curves is further evaluated; however, prior to this discussion the effect of training on the critical transformation temperatures and the ΔS^transf. is firstly examined. This is motivated on the one hand by the influence of the training process on the critical transformation temperatures [20] what then necessities a careful assessment of the thermal behavior of the trained Ni-Mn-Sn in order to ensure an appropriate choice of operating temperatures for strain studies. On the other hand, such an examination contributes valuable information in terms of ΔS behavior pertinent to ECE. Henceforth, the specimen was subjected to mechanical training, which was conducted at room temperature according to the procedures described previously [16, 17]. In result, a single-variant and a two-variant single-crystalline samples were produced. Both samples were subsequently DSC scanned along with a self-accommodated, multivariant sample. The results of the DSC measurements are presented in Fig. 2. The measurement in each case was carried out by first cooling the sample to 100 K (no curves) and then recording the curves first on heating up to 473 K, then on cooling down to 100 K at which temperature the cycle was reversed. On the cooling and on the second heating runs, all three samples are found to exhibit typical exothermic and endothermic peaks referring to the forward and reverse MPTs. The peaks are typically broad, which is likely to stem from the single crystalline nature of the specimens [19]. Noteworthily on the first heating ramp, both endothermic peaks for the single-variant and the two-variant samples are shortened from the left side of the temperature axis as compared to the multivariant sample and to the second heating run for the same samples. The characteristic M_s, M_f, A_s and A_f temperatures are evaluated with the aid of the tangential method, and their values are given in Table 1, along with the peak temperatures of the forward and reverse MPTs. The values of the thermal hysteresis determined as ΔT_hyst. = A_s − M_f are also provided. The table lists in addition the equilibrium temperature T₀ evaluated as $ T_{0} = \frac{1}{2}\left( {M_{\text{s}} + A_{\text{f}} } \right) $ [21]. The magnitudes of the transformation entropy changes for the forward ($ \Delta S_{A \to M}^{{{\text{transf}} .}} $) and reverse ($ \Delta S_{A \leftarrow M}^{{{\text{transf}} .}} $) MPTs are also computed as

$$ \Delta S_{A \leftrightarrow M}^{{{\text{transf}} .}} = {\raise0.7ex\hbox{${\Delta H_{\text{DSC}}^{A \leftrightarrow M} }$} \!\mathord{\left/ {\vphantom {{\Delta H_{\text{DSC}}^{A \leftrightarrow M} } {T_{0} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${T_{0} }$}}, $$

(1)

where $ \Delta H_{\text{DSC}}^{A \leftrightarrow M} $ is the latent heat measured by DSC [22] and presented in Table 1. For better illustration, the evolution of the characteristic M_s, M_f, A_s and A_f temperatures and the $ \Delta S_{A \leftrightarrow M}^{{{\text{transf}}.}} $ upon the first and second heating/cooling cycles are portrayed in Fig. 3a, b, respectively. From both Table 1 and Fig. 3a, it is noticed that the M_s, M_f temperatures remain unscathed irrespective of the variant state of the sample. A minute increase in the M_s and a decrease in the M_f temperatures in the trained samples with respect to the untrained sample may result from the mechanical history of the former samples, whereby the training is coupled with dislocation emission and thus easies the MPT; hence, lower undercooling (M_s) and lower overheating (M_f) are necessary to induce the forward and reverse MPTs. On the other hand, the A_s temperatures for the single-variant and the two-variant samples increase abruptly upon the first heating cycle following strictly the compression tests. The A_s temperatures then assume lower values during the second heating experiment once the specimen has recovered the multivariant microstructure following the first heating experiment. The change in the A_s temperature between the first and second cycles, i.e, between the two-variant and/or a single-variant state and a multivariant condition is circa ΔA_s = 29 K. This effect may be understood in relation to the stress-induced stabilization of martensite [23, 24, 25, 26, 27], where in principle large lattice mismatch between the austenite and single-variant martensite upon reverse MPT requires a formation of twinned martensite plates at the interface region to accommodate local incompatibility between the parent and martensitic phases. As a result, thermally induced twinning stands in need of a more substantial overheating shifting the A_s to a higher temperature range. Interestingly, there is no further appreciable change in the A_s temperature between the two- and a single-variant state samples, most likely because in both cases the training has also produced a similar degree of stabilization. This strongly suggests that the coarse two-variant state cannot accommodate the elastic transformation strain, and thus, a more complex microstructure (self-accommodated-like) is needed to absorb the elastic energy along the habit plane. Similarly to the M_s and M_f temperatures, also the A_f temperature does not seem to respond to the stress-induced stabilization of martensite, which is more prone to affect the onset of the reverse transformation. An inferior discrepancy in the A_f temperatures between the first and second cycles as well as a minute increase in the A_f temperature and a decrease in the A_s (second cycle) relative to the multivariant state can be as before linked to the mechanical history of the sample. Overall mechanical training has a profound effect on the A_s temperature during the first heating cycle, which restores the variant degeneracy. This is then reflected in an extended transformation hysteresis ΔT_hyst. = A_s − M_f = 40 K, whereas in “normal” cases, that is without stabilization, trained and reheated specimens show slightly lower hysteresis than the original multivariant state (Table 1).

Figure 2
DSC curves recorded on heating and cooling for the Ni_49.5Mn_38.4Sn_12.2 single crystal in a self-accommodated, multivariant state (bottom); a two-variant state (middle); a single-variant state (top)

Table 1

Characteristic martensite start (M_s), martensite finish (M_f), austenite start (A_s) and austenite finish (M_f) temperatures along with the peak temperatures of the forward (T_pA→M) and reverse (T_pM→A) martensitic transformations presented together with the values of the equilibrium temperature T₀ = (M_s+ A_f)/2, the transformation hysteresis ΔT_hyst. = A_s−M_f and the magnitude of the transformation entropy changes upon forward ($ \Delta S_{A \to M}^{{{\text{transf}} .}} $) and reverse ($ \Delta S_{M \to A}^{{{\text{transf}} .}} $) MPTs

Specimen	Cycle	M _s	M _f	A _s	A _f	T _pA→M	T _pM→A	A_s−M_f	T ₀	$ \Delta S_{A \to M}^{{{\text{transf}} .}} $	$ \Delta S_{M \to A}^{{{\text{transf}} .}} $
Specimen	Cycle	(K)								(J/kg K)
Multi-var.	1st	348	305	317	364	328	343	12	356	48.4	43.3
Multi-var.	2nd	348	305	317	364	328	343	12	356	48.6	46.9
Two-var.	1st	355	299	339	368	325	341	40	361	41.5	38.4
Two-var.	2nd	355	300	310	372	324	339	10	364	43.0	42.6
Single-var.	1st	356	300	339	368	325	343	39	362	42.9	37.7
Single-var.	2nd	356	300	310	372	324	341	10	364	42.5	39.6

Figure 3
The critical M_s, M_f, A_s and A_f and transformation entropy changes dependencies on the variant state of the Ni_49.5Mn_38.4Sn_12.2 single crystal

Noteworthily, the $ \Delta S^{{{\text{transf}} .}} $ for both the forward and reverse MPTs decreases with decreasing number of martensite variants, what presumably relates to the energy dissipation and a release of elastic strain energy triggered by microstructure refinement. On this occasion, the magnetic contribution to the $ \Delta S^{{{\text{transf}}.}} $ is neglected owing to the $ T_{\text{C}}^{\text{A}} $ < A_s, whose temperature separation evidently extends with training, and frequently it is this close proximity between both temperatures, which accounts for varying $ \Delta S^{{{\text{transf}} .}} $ in metamagnetic systems, where $ T_{\text{C}}^{\text{A}} $ ≥ A_s [28]. In this instance, the difference in $ \Delta S^{{{\text{transf}} .}} $ between the forward and reverse transformations accounts for energy dissipation during the transformation process.

Based on the classical Clausius–Clapeyron relationship:

$$ \Delta S^{{{\text{transf}} .}} = - v_{0} \Delta \varepsilon^{{{\text{transf}} .}} \left( {\frac{{{\text{d}}T_{\text{MPT}} }}{{{\text{d}}\sigma }}} \right)^{ - 1} $$

(2)

where the $ v_{0} $ is the specific volume, 1.04 × 10⁻⁴ m³/kg (adopting the lattice parameter of the austenite phase [19]), $ \Delta \varepsilon^{{{\text{transf}} .}} $ is the martensitic transformation strain change, while the $ \frac{{{\text{d}}T_{\text{MPT}} }}{{{\text{d}}\sigma }} $ is the stress-driven shift in the MPT temperature (T_MPT), the isothermal entropy change for a given $ \Delta \varepsilon^{{{\text{transf}} .}} $ can be estimated and compared with the DSC results.

The $ \frac{{{\text{d}}T_{\text{MPT}} }}{{{\text{d}}\sigma }} $ is assigned the value of 0.19 K/MPa as derived from the inverse of the temperature dependence of $ \sigma_{{M_{\text{s}} }} $, i.e, $ \left( {\frac{{{\text{d}}\sigma_{{M_{\text{s}} }} }}{{{\text{d}}T}}} \right)^{ - 1} $, what is discussed later on in the text. According to Fig. 1 and assuming that the $ \Delta \varepsilon^{{{\text{transf}} .}} $ = 4.9%, the entropy production amounts to $ \Delta S^{{{\text{transf}} .}} $ = 26.4 J/kgK, which for the theoretical $ \Delta \varepsilon_{{{\text{theor}} .}}^{{{\text{transf}} .}} $ = 6.4% can yield up to 34.3 J/kgK, exceeding $ \Delta S $ in the comparable giant elastocaloric materials, e.g., Ni-Mn-In showing $ \Delta S^{{{\text{transf}} .}} $ = 6.4 J/kgK ($ \Delta \varepsilon^{{{\text{transf}} .}} = 1.1\% $) [11]. Within the thermodynamic framework, the total heat Q released or consumed upon the forward and reverse MPTs and measured by DSC breaks down to several inputs as outlined below [29]:

$$ -\,Q = -\, \Delta H_{{{\text{chem}} .}}^{{{\text{aust}} .\to {\text{mart}} .}} + \Delta H_{{{\text{elas}} .}}^{{{\text{aust}} .\to {\text{mart}} .}} + E_{{{\text{fr}} .}} $$

(3)

where $ \Delta H_{{{\text{chem}} .}}^{{{\text{aust}} .\to {\text{mart}} .}} $ is the chemical enthalpy constituting the primary driving force for MPT remaining constant due to the diffusionless nature of MPT, $ \Delta H_{{{\text{elas}} .}}^{{{\text{aust}} .\to {\text{mart}} .}} $ is the elastic enthalpy associated with elastic strain accommodation opposing the progress of MPT, whereas the $ E_{{{\text{fr}} .}} $ is the frictional work resulting from the movement of habit planes, etc., which is irreversible and lost to the system upon the transformation. Given the value of T₀ (Table 1), the chemical enthalpy for the forward and reverse MPTs can be estimated from the DSC measurements as [29]:

$$ \Delta H_{{{\text{chem}} .}}^{{{\text{aust}} .\to {\text{mart}} .}} \left( {T_{0} } \right) = T_{0} \mathop \smallint \limits_{{M_{\text{s}} }}^{{M_{\text{f}} }} \frac{{{\text{d}}Q_{{{\text{transf}} .}} }}{T} $$

(4)

$$ \Delta H_{{{\text{chem}} .}}^{{{\text{aust}} .\leftarrow {\text{mart}} .}} \left( {T_{0} } \right) = T_{0} \mathop \smallint \limits_{{A_{\text{s}} }}^{{A_{\text{f}} }} \frac{{{\text{d}}Q_{{{\text{transf}} .}} }}{T} $$

(5)

Alternatively, the chemical enthalpy can be also estimated with the aid of the Clausius–Clapeyron equation (Eq. 2) assuming $ \Delta \varepsilon_{{{\text{theor}} .}}^{{{\text{transf}} .}} $ = 7%, for the ideal [001] orientation, i.e., when α = 0, which then provides $ \Delta S_{{{\text{theor}} .}}^{{{\text{transf}} .}} $ = 37.7 J/kgK, what then is multiplied by T₀, estimated for example for the multivariant sample, leads to:

$$ -\,\Delta H_{{{\text{chem}} .}}^{{{\text{aust}} .\to {\text{mart}} .}} = T_{0} \Delta S^{{{\text{transf}} .}} = 13.4\,{\text{J}}/{\text{g}}. $$

(6)

Next it is assumed that the dissipated $ E_{{{\text{fr}} .}}^{{{\text{aust}} .\to {\text{mart}} .}} $ is approximated by the stress–strain curve loop area (Fig. 1) according to: [30]

$$ E_{{{\text{fr}} .}}^{{{\text{aust}} .\to {\text{mart}} .}} = \frac{{\oint {\sigma \left( \varepsilon \right){\text{d}}\varepsilon } }}{\rho }, $$

(7)

where ρ is the alloy’s density; ρ = 8.2 × 10³ kg/m³. And hence $ E_{{{\text{fr}} .}}^{{{\text{aust}} .\to {\text{mart}} .}} $ for the $ \Delta \varepsilon^{{{\text{transf}} .}} $ attaining 4.9% (Fig. 1) is determined to be equal to 0.7 J/g. Extrapolating $ \Delta \varepsilon^{{{\text{transf}} .}} $ to $ \Delta \varepsilon_{{{\text{theor}} .}}^{{{\text{transf}} .}} $ = 7%, the maximum frictional work accompanying the MPT is then estimated at 0.9 J/g. Given that the hysteresis loop area $ \oint {\sigma \left( \varepsilon \right){\text{d}}\varepsilon } $ is calculated upon the continuous loading and unloading cycle, only half of the computed $ E_{{{\text{fr}} .}}^{{{\text{aust}} .\to {\text{mart}} .}} $ is taken for further evaluation of energy contribution [25]. Following from Eq. 3, it is now possible to estimate the elastic enthalpy contribution associated with the forward MPT:

$$ \Delta H_{{{\text{elas}} .}}^{{{\text{aust}} .\to {\text{mart}} .}} = -\, Q_{{{\text{transf}} .}} + E_{{{\text{fr}} .}}^{{{\text{aust}} .\to {\text{mart}} .}} + T_{0} \mathop \smallint \limits_{{M_{\text{s}} }}^{{M_{\text{f}} }} \frac{{{\text{d}}Q_{{{\text{transf}} .}} }}{T}, $$

(8)

whereas for the reverse transformation:

$$ \Delta H_{{{\text{elas}} .}}^{{{\text{aust}} .\leftarrow {\text{mart}} .}} = -\, Q_{{{\text{transf}} .}} - E_{{{\text{fr}} .}}^{{{\text{aust}} .\to {\text{mart}} .}} + T_{0} \mathop \smallint \limits_{{M_{\text{s}} }}^{{M_{\text{f}} }} \frac{{{\text{d}}Q_{{{\text{transf}} .}} }}{T}. $$

(9)

Here the $ \Delta H_{{{\text{chem}} .}}^{{{\text{aust}} .\leftrightarrow {\text{mart}}}} $ is approximated employing Eq. 6 and hence $ \Delta H_{{{\text{elas}} .}}^{{{\text{aust}} .\leftarrow {\text{mart}} .}} $:

$$ \Delta H_{{{\text{elas}} .}}^{{{\text{aust}} .\leftrightarrow {\text{mart}} .}} = -\, Q_{{{\text{transf}} .}} \mp E_{{{\text{fr}} .}}^{{{\text{aust}} .\to {\text{mart}} .}} + T_{0} \Delta S_{{{\text{C}} - {\text{C}}}}^{{{\text{transf}} .}} , $$

(10)

where for distinction ΔS has been attributed with the C–C subscript to indicate that it has been computed according to Eq. 2. The values of both the chemical and elastic enthalpy contributions computed for the multivariant, two-variant and single-variant specimens are presented in Table 2. The chemical enthalpy has been estimated according to Eq. 6 (C–C) and according to Eqs. 4 and 5 (DSC). It is found that the absolute value of $ \Delta H_{{{\text{elas}} .}} $ is on the whole lower on the forward MPT rather than on the reverse transformation. Interestingly $ \Delta H_{{{\text{elas}} .}} $ on the reverse MPT for the trained two- and single-variant specimens is also found lower on the first cycle than on the second. This indicates that the training processes stimulate elastic strain energy dissipation. It then implies that the shift in the A_s temperature in the trained samples should be chiefly associated with lower surface energy entailing larger and less mobile phase interface and thus a greater energy barrier for austenite restoration [29, 31]. At this point, it is also worth reemphasizing that the currently observed stabilization effect primarily affecting the A_s temperature but having essentially no influence on the A_f temperature, which is reproducible on the first and second heating runs, somewhat differs from the more traditionally reported stabilization phenomena [23, 24, 25, 26, 27]. Typically the mechanical stabilization effect [23, 24, 25, 26, 27] refers to the shift in A_s well above the A_f of the destabilized state, unlike here. It thus corroborates that the mechanical modification of microstructure toward a two- or a single-variant state leading to a shift in the A_s temperature is linked to the release of the elastic strain energy stored in the multivariant state what then necessitates greater overheating to initiate retransformation and contributes to the shift in A_s.

Table 2

The forward ($ \Delta H_{{{\text{chem}} .}}^{{{\text{aust}} .\to {\text{mart}} .}} $) and reverse ($ \Delta H_{{{\text{chem}} .}}^{{{\text{aust}} .\leftarrow {\text{mart}} .}} $) chemical and elastic ($ \Delta H_{{{\text{elas}} .}}^{{{\text{aust}} .\to {\text{mart}} .}} $, $ \Delta H_{{{\text{elas}} .}}^{{{\text{aust}} .\leftarrow {\text{mart}} .}} $) enthalpies computed based on the Clausius–Clapeyron (C–C) relationship and DSC measurements (DSC) for the multivariant, two-variant and the single-variant Ni_49.5Mn_38.4Sn_12.2 single-crystal specimens

Energy input	Method	Cycle	Multivariant	Two-variant	Single-variant
Energy input	Method	Cycle	J/g
$ \Delta H_{{{\text{chem}} .}}^{{{\text{aust}} .\to {\text{mart}} .}} $	C–C	1st	13.4	13.6	13.6
	C–C	2nd	13.4	13.7	13.7
	DSC	1st	18.8	16.6	17.1
	DSC	2nd	18.8	17.4	17.1
$ \Delta H_{{{\text{chem}} .}}^{{{\text{aust}} .\leftarrow {\text{mart}} .}} $	DSC	1st	16.1	14.2	14.0
	DSC	2nd	17.5	16.5	15.4
$ \Delta H_{{{\text{chem}} .}}^{{{\text{aust}} .\to {\text{mart}} .}} $	–	1st	3.4	0.9	1.4
	–	2nd	3.4	1.5	1.3
$ \Delta H_{{{\text{elas}} .}}^{{{\text{aust}} .\leftarrow {\text{mart}} .}} $	–	1st	2.5	0.7	0.5
	–	2nd	3.8	2.3	1.2

The temperature dependency of the compressive stress-compressive strain curves for the studied Ni_49.5Mn_38.4Sn_12.2 [001] single crystal was evaluated by performing the straining tests every 10 K starting from 343 K until 373 K. The results are given in Fig. 4. The maximum applied strain was limited to 4.3% for the cycles made at 343, 353 and 363 K, whereas for the cycle made at 373 K the maximum applied strain was increased to 6%. Before each cycle, the sample was heated up to 473 K and left for 10 min to equilibrate before cooling to the T_test at which temperature it was once again left for 10 min to stabilize.

Figure 4
Isothermal-compressive stress-compressive strain curves measured at 343, 353, 363 and 373 K upon loading and unloading the Ni_49.5Mn_38.4Sn_12.2 single crystal at the strain rate of 3.7 × 10⁻⁴ s⁻¹

With the exception for the sample tested at 343 K, all the other curves demonstrate a recoverable superelastic response (Fig. 4). The sample tested at 343 K fails to respond superelastically, since in this instance the test has been conducted at the T_test ≤ M_s< A_f temperature regime, what implicates that even despite the initial overheating to 473 K after the compression the specimen remains partially in the martensite state and thus it is unable to completely retransform to austenite. Subsequent reheating to 473 K and then a careful inspection of the sample size confirmed that there was no permanent plastic deformation involved, and upon reheating a perfect shape memory effect took place. The residual strain was thus most likely associated with the detwinning of martensite. Otherwise with respect to the other test temperatures, the σ_cr. increases with increasing temperature what is ascribable to an expanding temperature gap between the T_test and M_s [32], and this phenomenon is well explained within the framework of the classical Clausius–Clapeyron relationship (Eq. 2). The linear dependence of the σ_cr. on temperature is portrayed in Fig. 5a, and it has the slope of 5.6 MPa K⁻¹, which is slightly below the $ \frac{{{\text{d}}\sigma_{{{\text{cr}} .}} }}{{{\text{d}}T}} $ found for the polycrystalline Mn_48.7Ni_42.1Sn_9.2 (5.8 MPa/K) [14] and exceeds the $ \frac{{{\text{d}}\sigma_{{{\text{cr}} .}} }}{{{\text{d}}T}} $ slope found for the Ni₄₅Mn_36.5Co₅In_13.5 [100] single crystal (2.1 MPa K⁻¹) [33]. The stress hysteresis and hysteresis loop decreased with increasing T_test suggesting that with an increasing temperature and under the given strain-limited conditions less austenite transformed to martensite phase. This is well illustrated in Fig. 6 portraying hysteresis loss dependence on martensite fraction. The hysteresis loss in Fig. 6 is determined as the loop area for the temperature-dependent compression tests (Fig. 4), whereas the martensite fraction is determined as the ratio between the transformation entropy computed according to the Clausius–Clapeyron relationship for a given experimentally determined transformation strain ($ \Delta S_{{{\text{C}} - {\text{C}}}}^{{{ \exp } .}} $) and the theoretical $ \Delta S_{{{\text{C}} - {\text{C}}}}^{{{\text{theor}} .}} $ computed assuming $ \Delta \varepsilon_{{{\text{theor}} .}}^{{{\text{transf}} .}} = 7\% $. Data points collected under test conditions when the applied strain was limited to 4.3% are presented as circles in Fig. 6, whereas the experimental point when the applied strain was increased to 6% is presented as a square. The fitting in Fig. 6 has been restricted to points determined at 343, 353 and 363 K. A parallel evolution between hysteresis loss and martensite fraction with temperature can be readily noticed from the figure, suggesting mutual correlation between these two parameters. In analogy to Fig. 4, the effect of cycling on the evolution of the compressive stress is presented in Fig. 7. The test was carried out at 363 K following preheating to 473 K and equilibration after cooling to 363 K. Afterward the cycles run continuously. From Fig. 7, it comes to light that the σ_cr. decreases with every next cycle. The slope (Fig. 5b) is determined to have the value of − 18.1 MPa n⁻¹, where n is the cycle number. The sample degraded following the fifth cycle, what made it impossible to determine the $ \frac{{{\text{d}}\sigma_{{{\text{cr}} .}} }}{{{\text{d}}T}} $ saturation point, since often following a certain number of cycles the $ \frac{{{\text{d}}\sigma_{{{\text{cr}} .}} }}{{{\text{d}}T}} $ slope is found to level off [34]. An SEM image portraying a typical brittle fracture, which was taken from the specimen after the fifth cycle test, is shown in the inset (a) in Fig. 7. Whereas the inset (b) in that figure shows the DSC scans measured for the initial multivariant state (Fig. 2) and for the specimen after the fifth, degrading compression cycle (Fig. 7). After the fifth compression, the DSC peaks become narrower relative to the initial multivariant state, peaks were measured on two DSC cycles, and they show jerky characteristic and smaller peak area what altogether suggests discontinuities in the sample, consistent with observed fracturing. These results reiterate the critical issue, which lies in more general with ordered Heusler systems and which is their propensity to cracking and limited fatigue life. However, challenging this awkward limitation may turn out susceptible to engineering [23, 35].

Figure 5
Temperature-dependent (a) and cycle number-dependent (b) compressive stress for Ni_49.5Mn_38.4Sn_12.2 single crystal

Figure 6
The MPT hysteresis loss determined as the loop area for the temperature-dependent compression tests versus martensite fraction ($ f_{{{\text{mart}} .}} $) determined as the ratio between the transformation entropy computed according to the Clausius–Clapeyron relationship for a given experimentally determined transformation strain ($ \Delta S_{{{\text{C}} - {\text{C}}}}^{{{ \exp } .}} $) and the theoretical $ \Delta S_{{{\text{C}} - {\text{C}}}}^{{{\text{theor}} .}} $ computed assuming $ \Delta \varepsilon_{{{\text{theor}} .}}^{{{\text{transf}} .}} = 7\% $. Circle denotes experimental points when the applied strain was limited to 4.3%, whereas square is associated with the test performed at 373 K when the strain was increased to 6%. See text for details

Figure 7
Isothermal compressive stress-compressive strain curves repeated five times at 363 K upon loading and unloading the Ni_49.5Mn_38.4Sn_12.2 single crystal at the strain rate of 3.7 × 10⁻⁴ s⁻¹

The observed drop in the σ_cr with increasing cycle number is owed to the training phenomena [32], whereby the microstructure undergoes an appreciable makeover. The extent of microstructure change can be assessed based on Figs. 8 and 9 showing EBSD and BSE images taken from the Ni_49.5Mn_38.4Sn_12.5 single crystal in a self-accommodated state (Fig. 8) and following superelastic training (Fig. 9). In a self-accommodated state, the microstructure is typically organized at several length scales and incorporates distinct sub-macro- and sub-microstructural features including twin variant colonies (TWC), interplate boundaries (IPB), twin boundaries (TB), etc., for more details see [17]. Following the superelastic training, the microstructure undergoes pronounced refinement. On the macroscale, the training results in the disappearance of TWC, whereas IPBs advance to a twin relation as visualized by distinct and straight interplate interfaces. On the other hand, a much higher density of the (100) modulation boundaries (MB) [17] can be observed after superelastic cycling providing additional degree of freedom for lattice strain accommodation. They create parallel and cross-configurations showing large boundary curvatures and step-like character associated with strain accommodation (Figs. 9b–d). Comparing with the initial microstructure and that obtained after superelastic training, it can be concluded that a considerable amount of fine TBs are replaced by MBs. As a consequence of the removal of fine TBs (or partial removal, Fig. 9c), the thick IPB variants rotate toward the common K₁ twinning plane. An analogous situation takes place in the case of a more conventional training process where detwinning of fine twins (shown in Fig. 8b) causes an additional lattice rotation bringing the major variants into perfect twin relation [17]. A closer inspection with a TEM demonstrates the extent of microstructure rearrangement on a sub-micrometer scale. Example bright-field (BF) TEM images are provided in Fig. 10a, b for illustration. The images were taken at room temperature from the superelastically cycled specimen after the fifth and degrading cycle. Clearly, the microstructure undergoes prominent refinement showing finer martensite plates with a more distinct and sharp interfaces relative to the self-accommodated state [17].

Figure 8
EBSD image of a self-accommodated microstructure in the Ni_49.5Mn_38.4Sn_12.2 single crystal (a) and the back-scattered electron (BSE) image (b) showing fine twin microstructure of chosen individual lamella observed in the EBSD map in a

Figure 9
BSE (a, b) and EBSD (c, d) microstructures taken from Ni_49.5Mn_38.4Sn_12.2 single crystal following a superelastic compression test

Figure 10
BF images a, b together with corresponding SADPs c, d taken form the Ni_49.5Mn_38.4Sn_12.2 single crystal after the fifth compression cycle

Overall, it is shown that despite its intrinsic brittleness the Ni-Mn-Sn system warrants further investigation given the relatively large transformation entropy accompanying the MPT in this system. Figure 11 brings together the absolute values of the adiabatic temperature change (ΔT_ad.) plotted as function of the transformation entropy change (ΔS) for a number of different shape memory alloys [36]. Although this is merely a schematic representation, it nonetheless affords a qualitative overview of the relative cooling potential depending on the ΔS for different systems. The considerable values of the ΔS encountered in the Ni-Mn-Sn system (~ 50 J/kgK) in addition to its MCE potential allow to reasonably speculate that this system might be a prospective candidate for multiferroic cooling applications, provided that its limited mechanical performance is substantially improved.

Figure 11
Absolute values of the adiabatic temperature change (ΔT_ad.) versus transformation entropy change—absolute (ΔS) for a number of shape memory alloy systems

Summary

The near [001]-oriented Ni_49.5Mn_38.4Sn_12.5 single crystal has been subjected to compressive straining. It showed a very promising superplastic response at the temperature of 363 K and above (≥ A_f). The maximum transformation strain attained at 363 K was determined at the value of 4.9%, which is less than the theoretical 7%. The compressive stress increased with the test temperature at the rate of 5.6 MPa/K, whereas it decreased upon cycling at the rate of 18.1 MPa/cycle. After the fifth cycle, the specimen degraded, revealing typical signs of brittle fracture. Upon superplastic cycling, the microstructure underwent considerable refinement with increasing activity of modulation boundaries presumably responsible for the decrease in compressive stress. Martensite training leading to a single-variant microstructure and stimulating dissipation of the elastic strain energy has a profound influence on the A_s temperature and on the thermal hysteresis what presents an opportunity for future engineering of Ni-Mn-based SMA.

Notes

Acknowledgements

The financial support from the Polish National Science Centre (NCN)—Project Number: 2012/07/N/ST8/03918 is gratefully acknowledged.

Compliance with ethical standards

Conflict of interest

The authors declare that they have no conflict of interest.

References

1.
Planes A, Manosa L, Acet M (2009) Magnetocaloric effect and its relations to shape-memory properties in ferromagnetic Heusler alloys. J Phys Condens Mater 21:233201-1–233201-28CrossRefGoogle Scholar
2.
Chernenko VA, L’vov VA, Cesari E, Kosogor A, Barandiaran JM (2013) Transformation volume effects on shape memory alloys. Metals 3:237–282CrossRefGoogle Scholar
3.
Karaca HE, Karaman I, Basaran B, Lagoudas DC, Chumlyakov YI, Maier HJ (2007) On the stress-assisted magnetic-field-induced phase transformation in Ni₂MnGa ferromagnetic shape memory alloys. Acta Mater 55:4253–4269CrossRefGoogle Scholar
4.
Kustov S, Corro ML, Pons J, Cesari E (2009) Entropy change and effect of magnetic field on martensitic transformation in a metamagnetic Ni–Co–Mn–In shape memory alloy. Appl Phys Lett 94:191901-1–191901-3CrossRefGoogle Scholar
5.
Entel P, Dannenberg A, Siewert M, Herper HC, Gruner ME, Buchelnikov VD, Chernenko VA (2011) Composition-dependent basics of smart Heusler materials from first-principles calculations. Mater Sci Forum 684:1–29CrossRefGoogle Scholar
6.
Bruno NM, Huang YJ, Dennis CL, Li JG, Shull RD, Ross JH Jr, Chumlyakov YI, Karaman I (2016) Effect of grain constraint on the field requirement for magnetocaloric effect in Ni₄₅Co₅Mn₄₀Sn₁₀ melt-spun ribbons. J Appl Phys 120:075101-1–075101-9CrossRefGoogle Scholar
7.
Krenke T, Duman E, Acet M, Wassermann EF, Moya X, Manosa L, Planes A (2005) Inverse magnetocaloric effect in ferromagnetic Ni–Mn–Sn alloys. Nat Mater 4:450–454CrossRefGoogle Scholar
8.
Castillo-Villa PO, Manosa L, Planes A, Soto-Parra DE, Sanchez-Llamazares JL, Flores-Zuniga H, Frontera C (2013) Elastocaloric and magnetocaloric effects in Ni–Mn–Sn(Cu) shape-memory alloy. J Appl Phys 113:053506-1–053506-6CrossRefGoogle Scholar
9.
Fahler S, Rossler UK, Kastner O, Eckert J, Eggeler G, Emmerich H, Entel P, Muller S, Quandt E, Albe K (2012) Caloric effects in ferroic materials: new concepts for cooling. Adv Eng Mater 14:10–19CrossRefGoogle Scholar
10.
Sun W, Liu J, Lu B, Li Y, Yan A (2016) Large elastocaloric effect at small transformation strain in Ni₄₅Mn₄₄Sn₁₁ metamagnetic shape memory alloys. Scr Mater 114:1–4CrossRefGoogle Scholar
11.
Huang YJ, Hu QD, Bruno NM, Chen JH, Karaman I, Ross JH Jr, Li JG (2015) Giant elastocaloric effect in directionally solidified Ni–Mn–In magnetic shape memory alloy. Scr Mater 105:42–45CrossRefGoogle Scholar
12.
Li Y, Sun W, Zhao D, Xu H, Liu J (2017) An 8 K elastocaloric temperature change induced by 1.3% transformation strain in Ni₄₄Mn_45−xSn₁₁Cu_x alloys. Scr Mater 130:278–282CrossRefGoogle Scholar
13.
Xiao F, Jin M, Liu J, Jin X (2015) Elastocaloric effect in Ni₅₀Fe₁₉Ga₂₇Co₄ single crystals. Acta Mater 96:292–300CrossRefGoogle Scholar
14.
Turabi AS, Lazpita P, Sasmaz M, Karaca HE, Chernenko VA (2016) Magnetic and conventional shape memory behavior of Mn–Ni–Sn and Mn–Ni–Sn(Fe) alloys. J Phys D Appl Phys 49:205002-1–205002-8CrossRefGoogle Scholar
15.
Alvarez-Alonso P, Aguilar-Ortiz CO, Villa E, Nespoli A, Flores-Zuniga H, Chernenko VA (2017) Conventional and inverse elastocaloric effect in Ni–Fe–Ga and Ni–Mn–Sn ribbons. Scr Mater 128:36–40CrossRefGoogle Scholar
16.
Czaja P, Szczerba MJ, Chulist R, Bałanda M, Przewoźnik J, Chumlyakov YI, Schell N, Kapusta Cz, Maziarz W (2016) Martensitic transition, structure and magnetic anisotropy of martensite in Ni–Mn–Sn single crystal. Acta Mater 118:213–220CrossRefGoogle Scholar
17.
Czaja P, Chulist R, Szlezynger M, Skuza W, Chumlyakov YI, Szczerba MJ (2017) Self-accommodated and pre-strained martensitic microstructure in single-crystalline, metamagnetic Ni–Mn–Sn Heusler alloy. J Mater Sci 52:5600–5610. https://doi.org/10.1007/s10853-017-0793-3 CrossRefGoogle Scholar
18.
Perez-Sierra AM, Bruno NM, Pons J, Cesari E, Karaman I (2016) Atomic order and martensitic transformation entropy change in Ni–Co–Mn–In metamagnetic shape memory alloys. Scr Mater 110:61–64CrossRefGoogle Scholar
19.
Czaja P, Chulist R, Szczerba MJ, Przewoźnik J, Olejnik E, Chrobak A, Maziarz W, Cesari E (2016) Magnetostructural transition and magnetocaloric effect in highly textured Ni–Mn–Sn alloy. J Appl Phys 119:165102-1–165102-6CrossRefGoogle Scholar
20.
Pagounis E, Laptev A, Szczerba MJ, Chulist R, Laufenberg M (2015) Structural behavior and magnetic properties of a Ni–Mn–Ga single crystal across the martensite/austenite two-phase region. Acta Mater 89:32–40CrossRefGoogle Scholar
21.
Wayman CM, Tong HC (1977) On the equilibrium temperature in thermoelastic martensitic transformations. Scr Metall 11:341–343CrossRefGoogle Scholar
22.
Cesari E, Salas D, Kustov S (2011) Entropy changes in ferromagnetic shape memory alloys. Mater Sci Forum 684:49–60CrossRefGoogle Scholar
23.
Liua Y, Liu Y, Van Humbeeck J (1998) Two-way shape memory effect developed by martensite deformation in NiTi. Acta Mater 47:199–209CrossRefGoogle Scholar
24.
Šittner P, Novák V, Zárubová N (1998) Martensitic transformations in [001] CuAlZnMn single crystals. Acta Mater 46:1265–1281CrossRefGoogle Scholar
25.
Liu Y, Favier D (2000) Stabilisation of martensite due to shear deformation via variant reorientation in polycrystalline NiTi. Acta Mater 48:3489–3499CrossRefGoogle Scholar
26.
Picornell C, Pons J, Cesari E (2001) Stabilisation of martensite by applying compressive stress in Cu–Al–Ni single crystals. Acta Mater 49:4221–4230CrossRefGoogle Scholar
27.
Picornell C, Pons J, Cesari E (2006) Mechanical stabilisation and anomalous behaviour of the stress–strain loops in Cu–Al–Ni single crystals. Scr Mater 54:459–463CrossRefGoogle Scholar
28.
Segui C, Cesari E (2012) Composition and atomic order effects on the structural and magnetic transformations in ferromagnetic Ni–Co–Mn–Ga shape memory alloys. J Appl Phys 111:043914-1–043914-7CrossRefGoogle Scholar
29.
Ortin J, Planes A (1988) Thermodynamic analysis of thermal measurements in thermoelastic martensitic transformations. Acta Metall 36:1873–1889CrossRefGoogle Scholar
30.
Xu S, Huang HY, Xie J, Takekawa S, Xu X, Omori T, Kainuma R (2016) Giant elastocaloric effect covering wide temperature range in columnar-grained Cu_71.5Al_17.5Mn₁₁ shape memory alloy. APL Mater 4:106106-1–106106-7CrossRefGoogle Scholar
31.
Ahlers M, Pascual R, Rapacioli R (1977) Transformation hardening and energy dissipation in martensite β-brass. Mater Sci Eng 27:49–55CrossRefGoogle Scholar
32.
Ma J, Karaman I, Noebe RD (2010) High temperature shape memory alloys. Int Mater Rev 55:257–315CrossRefGoogle Scholar
33.
Karaca HE, Karaman I, Brewer A, Basaran B, Chumlyakov YI, Maier HJ (2008) Shape memory and pseduelasticity response of NiMnCoIn magnetic shape memory alloy single crystals. Scr Mater 58:815–818CrossRefGoogle Scholar
34.
Yang Z, Cong DY, Sun XM, Nie ZH, Wang YD (2017) Enhanced cyclability of elastocaloric effect in boron-microalloyed Ni–Mn–In magnetic shape memory alloys. Acta Mater 127:33–42CrossRefGoogle Scholar
35.
Hamilton RF, Sehitoglu H, Chumlyakov IY, Maier HJ (2004) Stress dependence of the hysteresis in single crystal Ni–Ti. Acta Mater 52:3383–3402CrossRefGoogle Scholar
36.
Chauhan A, Patel S, Vaish R, Bowen ChR (2015) A review and analysis of the elasto-caloric effect for solid-state refrigeration devices: challenges and opportunities. MRS Energy Sustain Rev J 2:1–18CrossRefGoogle Scholar

Copyright information

Open AccessThis article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.

Authors and Affiliations

P. Czaja
- 1
Email authorView author's OrcID profile
R. Chulist
- 1
T. Tokarski
- 2
T. Czeppe
- 1
Y. I. Chumlyakov
- 3
E. Cesari
- 4

1.Institute of Metallurgy and Materials SciencePolish Academy of SciencesKrakówPoland
2.Academic Centre of Materials and NanotechnologyAGH University of Science and TechnologyKrakówPoland
3.Siberian Physical-Technical InstituteTomskRussia
4.Departament de FisicaUniversitat de les Illes BalearsPalma de MallorcaSpain

Superelastic behavior of a metamagnetic Ni–Mn–Sn single crystal

Abstract

Introduction

Experimental

Results and discussion

Summary

Notes

Acknowledgements

Compliance with ethical standards

Conflict of interest

References

Copyright information

Authors and Affiliations

Personalised recommendations

Cite article

Cookies