Skip to main content
SpringerLink
Log in

Multi-scale finite element analysis for tension and ballistic penetration damage characterizations of 2D triaxially braided composite

  • Composites
  • Published:
Journal of Materials Science Aims and scope Submit manuscript

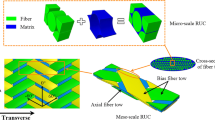
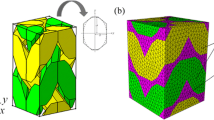
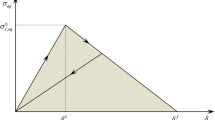
Abstract

The multi-scale finite element model is presented to analyze tension and ballistic penetration damage characterizations of 2D triaxially braided composite (2DTBC). At the mesoscopic level, the damage of fiber tows is initiated with 3D Hashin criteria, and the damage initiation of pure matrix is predicted by the modified von Mises. The progressive degradation scheme and energy dissipation method are adopted to capture softening behaviors of tow and matrix. The macro-scale damage model is established by maximum-stress criteria and exponential damage evolution. To simulate interface debonding and inter-ply delamination, a triangle traction–separation law is adopted in each scale. Both scale damage models are verified with available experimental results. Based on numerical predictions, the stress–strain responses and damage developments of 2DTBC under axial and transverse tension loading are studied. For ballistic penetration loading, the meso-scale damage mechanisms of 2DTBC are predicted using 1/4 model, 1/2 model, 1-layer model, 2-layer model and 3-layer model. Then, effects of different model and impactor radius on damage modes are analyzed. Additionally, the macro-scale ballistic penetration behaviors of 2DTBC are simulated and compared with experiment. The prediction results for tension and penetration correlate well with experiment results. Both tension and penetration damage characterizations for tow, matrix within tow, pure matrix, interface and inter-ply delamination are revealed. A comparison of penetration damage between meso- and macro-scale presents a similar crack mechanism between two scales.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Figure 1
Figure 2
Figure 3
Figure 4
Figure 5
Figure 6
Figure 7
Figure 8

(Reproduced with permission from [18])

Figure 9
Figure 10
Figure 11

(Reproduced with permission from [18])

Figure 12
Figure 13
Figure 14

(Reproduced with permission from [27])

Figure 15
Figure 16
Figure 17
Figure 18
Figure 19
Figure 20
Figure 21
Figure 22
Figure 23
Figure 24

Similar content being viewed by others

References

  1. Zhou L, Zeng J, Jiang L, Hu H (2018) Low-velocity impact properties of 3D auxetic textile composite. J Mater Sci 53(5):3899–3914

    Article  Google Scholar 

  2. Yang CH, Ma WN, Ma DW (2018) Low-velocity impact analysis of carbon nanotube reinforced composite laminates. J Mater Sci 53(1):637–656

    Article  Google Scholar 

  3. Ren Y, Zhang S, Jiang H, Xiang J (2018) Meso-scale progressive damage behavior characterization of triaxial braided composites under quasi-static tensile load. Appl Compos Mater 25(2):335–352

    Article  Google Scholar 

  4. Zhang C, Xu X (2013) Finite element analysis of 3D braided composites based on three unit-cells models. Compos Struct 98(3):130–142

    Article  Google Scholar 

  5. Kaboglu C, Mohagheghian I, Zhou J, Guan Z, Cantwell W, John S, Blackman BRK, Kinloch AJ, Dear JP (2017) High-velocity impact deformation and perforation of fibre metal laminates. J Mater Sci 53:4209–4228

    Article  Google Scholar 

  6. Xu L, Huang Y, Zhao C, Ha SK (2016) Progressive failure prediction of woven fabric composites using a multi-scale approach. Int J Damage Mech 27:97–119

    Article  Google Scholar 

  7. Key CT, Schumacher SC, Hansen AC (2007) Progressive failure modeling of woven fabric composite materials using multicontinuum theory. Compos Part B Eng 38(2):247–257

    Article  Google Scholar 

  8. Pan Z, Gu B, Sun B, Xiong J (2017) Progressive failure of 3-D textile composites under impact loadings. Compos Struct 168:710–724

    Article  Google Scholar 

  9. Zhang C, Curiel-Sosa JL, Duodu EA (2017) Finite element analysis of the damage mechanism of 3D braided composites under high-velocity impact. J Mater Sci 52(8):1–17

    Google Scholar 

  10. Xiao X, Kia HG, Gong XJ (2011) Strength prediction of a triaxially braided composite. Compos Part A Appl Sci Manuf 42(8):1000–1006

    Article  Google Scholar 

  11. Goldberg RK, Blinzler BJ, Binienda WK (2010) Modification of a macromechanical finite-element based model for impact analysis of triaxially-braided composites. J Aerosp Eng 25(3):383–394

    Article  Google Scholar 

  12. Goldberg RK, Blinzler BJ, Binienda WK (2010) Investigation of a macromechanical approach to analyzing triaxially-braided polymer composites. AIAA J 49(1):205–215

    Article  Google Scholar 

  13. Blinzler BJ, Goldberg RK, Binienda WK (2012) Macroscale independently homogenized subcells for modeling braided composites. AIAA J 50(9):1873–1884

    Article  Google Scholar 

  14. Zhang C, Li N, Wang W, Binienda WK, Fang H (2015) Progressive damage simulation of triaxially braided composite using a 3D meso-scale finite element model. Compos Struct 125:104–116

    Article  Google Scholar 

  15. Binienda WK, Li X (2010) A mesomechanical model for numerical study of two dimensional triaxially braided composite. J Eng Mech 136(11):1366–1379

    Article  Google Scholar 

  16. Zhang C, Binienda WK, Kohlman LW (2014) Analytical model and numerical analysis on the elastic behavior of triaxial braided composites. J Aerosp Eng 27(3):473–483

    Article  Google Scholar 

  17. Song S, Waas AM, Shahwan KW, Xiao X, Faruque O (2007) Braided textile composites under compressive loads: modeling the response, strength and degradation. Compos Sci Technol 67(15):3059–3070

    Article  Google Scholar 

  18. Li X, Binienda WK, Goldberg RK. Finite element model for failure study of two dimensional triaxially braided composite. NASA/TM-2010-216372

  19. Wang C, Zhong Y, Adaikalaraj PFB, Ji X, Roy A, Silberschmidt VV (2016) Strength prediction for bi-axial braided composites by a multi-scale modelling approach. J Mater Sci 51(12):6002–6018

    Article  Google Scholar 

  20. Zhang C, Binienda WK, Goldberg RK, Goldberg RK, Kohlman LW (2014) Meso-scale failure modeling of single layer triaxial braided composite using finite element method. Compos Part A Appl Sci Manuf 58(58):36–46

    Article  Google Scholar 

  21. Zhang C, Binienda WK (2014) A meso-scale finite element model for simulating free-edge effect in carbon/epoxy textile composite. Mech Mater 76(9):1–19

    Google Scholar 

  22. Zhang C, Binienda WK (2014) Numerical analysis of free-edge effect on size-influenced mechanical properties of single-layer triaxially braided composites. Appl Compos Mater 21(6):841–859

    Article  Google Scholar 

  23. Ha-Minh C, Imad A, Boussu F, Kanit T (2016) Experimental and numerical investigation of a 3D woven fabric subjected to a ballistic impact. Int J Impact Eng 88:91–101

    Article  Google Scholar 

  24. Luan K, Sun B, Gu B (2013) Ballistic impact damages of 3-D angle-interlock woven composites based on high strain rate constitutive equation of fiber tows. Int J Impact Eng 57(1):145–158

    Article  Google Scholar 

  25. Nilakantan G, Keefe M, Bogetti TA, Jr JWG (2010) Multiscale modeling of the impact of textile fabrics based on hybrid element analysis. Int J Impact Eng 37(10):1056–1071

    Article  Google Scholar 

  26. Nie WZ, Binienda WK (2015) Effective mesomechanical modeling of triaxially braided composites for impact analysis with failure. Earth Space 503–512

  27. Littell JD, Binienda WK, Arnold WA, Roberts GD, Goldberg RK (2009) Effect of microscopic damage events on static and ballistic impact strength of triaxial braid composites. Compos Part A Appl Sci Manuf 40(12):1846–1862

    Article  Google Scholar 

  28. Li X, Binienda WK, Goldberg RK (2010) Finite element model for failure study of two dimensional triaxially braided composite. J Aero Eng 24(2):170–180

    Article  Google Scholar 

  29. Littell JD (2008) The experimental and analytical characterization of the macromechanical response for triaxial braided composite materials. Ph.D. dissertation, University of Akron

  30. Nobeen NS, Zhong Y, Francis BAP, Ji X, Chia ESM, Joshi SC, Chen Z (2016) Constituent materials micro-damage modeling in predicting progressive failure of braided fiber composites. Compos Struct 145:194–202

    Article  Google Scholar 

  31. Zhang C, Mao C, Zhou Y (2017) Meso-scale damage simulation of 3D braided composites under quasi-static axial tension. Appl Compos Mater 24(5):1179–1199

    Article  Google Scholar 

  32. Xia Z, Zhang Y, Ellyin F (2003) A unified periodical boundary conditions for representative volume elements of composites and applications. Int J Solids Struct 40(8):1907–1921

    Article  Google Scholar 

  33. Zhang C, Curiel-Sosa JL, Bui TQ (2017) Comparison of periodic mesh and free mesh on the mechanical properties prediction of 3D braided composites. Compos Struct 159:667–676

    Article  Google Scholar 

  34. Kassem GA, Weichert D (2009) Micromechanical material models for polymer composites through advanced numerical simulation techniques. Pamm 9(1):413–414

    Article  Google Scholar 

  35. Jiang H, Ren Y, Gao B, Xiang J, Yuan FG (2017) Design of novel plug-type triggers for composite square tubes: enhancement of energy-absorption capacity and inducing failure mechanisms. Int J Mech Sci 131–132:113–136

    Article  Google Scholar 

  36. Jiang H, Ren Y, Gao B (2017) Research on the progressive damage model and trigger geometry of composite waved beam to improve crashworthiness. Thin Wall Struct 119:531–543

    Article  Google Scholar 

  37. Ren Y, Jiang H, Gao B, Xiang J (2017) A progressive intraply material deterioration and delamination based failure model for the crashworthiness of fabric composite corrugated beam: parameter sensitivity analysis. Compos Part B Eng 135:49–71

    Article  Google Scholar 

  38. Hashin Z (1980) Failure criteria for unidirectional fiber composites. J Appl Mech 47(2):329–334

    Article  Google Scholar 

  39. Lu Z, Xia B, Yang Z (2013) Investigation on the tensile properties of three-dimensional full five-directional braided composites. Comput Mater Sci 77(3):445–455

    Article  Google Scholar 

  40. Lapczyk I, Hurtado JA (2007) Progressive damage modeling in fiber reinforced materials. Compos Part A 38(11):2333–2341

    Article  Google Scholar 

  41. Fang GD, Liang J, Wang B (2009) Progressive damage and nonlinear analysis of 3D four-directional braided composites under unidirectional tension. Compos Struct 89(1):126–133

    Article  Google Scholar 

  42. Matzenmiller A, Lubliner J, Taylor L (1995) A constitutive model for anisotropic damage in fiber-composites. Mech Mater 20:125–152

    Article  Google Scholar 

  43. Sokolinsky VS (2010) Numerical simulation of the crushing process of a corrugated composite plate. Compos Part A 42(9):1119–1126

    Article  Google Scholar 

  44. Maimí P, Camanho PP, Mayugo J-A, Dávila CG (2006) A thermodynamically consistent damage model for advanced composites. Technical Report NASA/TM-2006-214282, NASA

  45. Zhang C, Xu X (2013) Finite element analysis of 3D braided composites based on three unit-cells models. Compos Struct 98(3):130–142

    Article  Google Scholar 

  46. Alfano G, Sacco E (2010) Combining interface damage and friction in a cohesive-zone model. Int J Numer Methods Eng 68(5):542–582

    Article  Google Scholar 

  47. Zhang C, Curiel-Sosa JL, Bui TQ (2017) A novel interface constitutive model for prediction of stiffness and strength in 3D braided composites. Compos Struct 163:32–43

    Article  Google Scholar 

  48. Abaqus 6.10 Analysis user’s manual (2010) Dassault Systèmes

  49. Benzeggagh ML, Kenane M (1996) Measurement of mixed-mode delamination fracture toughness of unidirectional glass/epoxy composites with mixed-mode bending apparatus. Compos Sci Technol 56(4):439–449

    Article  Google Scholar 

  50. Zhang D, Chen L, Wang Y, Zhang L, Zhang Y, Yu K, Lu X, Sun J, Xiao X, Qian K (2017) Stress field distribution of warp-reinforced 2.5D woven composites using an idealized meso-scale voxel-based model. J Mater Sci 52:6814–6836

    Article  Google Scholar 

Download references

Acknowledgements

The authors acknowledge the financial supports from the National Natural Science Foundation of China (No. 11402011). The financial supports from Fundamental Research Funds for the Central Universities (No. 201401390741) are also gratefully acknowledged.

Author information

Authors and Affiliations

  1. State Key Laboratory of Advanced Design and Manufacturing for Vehicle Body, Hunan University, Changsha, 410082, Hunan, China

    Hongyong Jiang, Yiru Ren, Songjun Zhang & Zhihui Liu

  2. College of Mechanical and Vehicle Engineering, Hunan University, Changsha, 410082, Hunan, China

    Hongyong Jiang, Yiru Ren, Songjun Zhang & Zhihui Liu

  3. China Academy of Launch Vehicle Tehcnology, Beijing, 10076, China

    Lu Nie

Authors
  1. Hongyong Jiang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yiru Ren
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Songjun Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Zhihui Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Lu Nie
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

YR helped with the research guidance, technological guidance, quality check of paper and writing level and final decision for submission. HJ contributed to the survey, programming of user material, finite element modeling (preprocessing and post-processing), picture and data processing, damage analysis of meso-scale and macro-scale triaxially braided composite under the tension loading and ballistic impact loading and writing of full text. SZ assisted with the part of work research, dealing of numerical computation error, programming study and numerical result discussion of meso-scale axial tension and transverse tension. ZL involved in numerical result discussion of meso-scale ballistic impact failure. LN contributed to the technological guidance.

Corresponding author

Correspondence to Yiru Ren.

Ethics declarations

Conflict of interest

The authors declared no potential conflict of interest with respect to the research, authorship and/or publication of this article.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Jiang, H., Ren, Y., Zhang, S. et al. Multi-scale finite element analysis for tension and ballistic penetration damage characterizations of 2D triaxially braided composite. J Mater Sci 53, 10071–10094 (2018). https://doi.org/10.1007/s10853-018-2248-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10853-018-2248-x

Keywords

Search

Navigation