Skip to main content
SpringerLink
Log in

The role of partial grain boundary dislocations in grain boundary sliding and coupled grain boundary motion

  • Published:
Journal of Materials Science Aims and scope Submit manuscript

Abstract

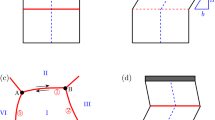
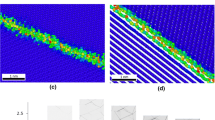
We study the process of grain boundary sliding through the motion of grain boundary dislocations, utilizing molecular dynamics and embedded atom method (EAM) interatomic potentials. For a Σ = 5 [001]{310} symmetrical tilt boundary in bcc Fe, the sliding process was found to occur through the nucleation and glide of partial grain boundary dislocations, with a secondary grain boundary structure playing an important role in the sliding process. While the homogeneous nucleation of these grain boundary dislocations requires shear strain levels higher than 7%, preexisting grain boundary dislocations are shown to glide at applied shear levels of 1.5%. The glide of the dislocations results in coupled motion of the boundary in the directions parallel and perpendicular to itself. Finally, interstitial impurities and vacancies were introduced in the grain boundary to study the effects on the sliding resistance of the boundary. While vacancies and H interstitials act as preferred nucleation sites, C interstitials do not. Both hydrogen and C interstitials stop dislocation glide whereas vacancies do not. A detailed study of the dynamic properties of these dislocations is also presented.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

References

  1. Van Swygenhoven H, Caro A Farkas D (2001) Scr Materialia 44(8–9):1513

    Article  Google Scholar 

  2. Pond RC, Hirth JP (1994) Solid State Physics – Adv Res Appl 47:287

    CAS  Google Scholar 

  3. Van Swygenhoven H, Derlet PA (2001) Phys Rev B 64(22)

  4. Hoagland RG, Kurtz R (2002) Philos Mag A – Phy Cond Matter Struct Defects Mech Prop 82(6):1073

    CAS  Google Scholar 

  5. Farkas D, Curtin WA (2005) MSE&A 412(1–2):316

    Article  Google Scholar 

  6. Winning M (2004) Zeitschrift Fur Metallkunde 95(4):233

    Article  CAS  Google Scholar 

  7. Kurtz RJ, Hoagland R, Hirth JP (1999) Philos Mag A – Phy Cond Matter Struct Defects Mech Prop 79(3):665

    CAS  Google Scholar 

  8. Sheikh Ali AD (1997) Acta Mater 45(8):3109

    Article  CAS  Google Scholar 

  9. Sagalowic L, Clark WAT (1996) Interface Sci 4(1–2):29

    Google Scholar 

  10. Bollmann W (1981) Philos Mag A – Phy Cond Matter Struct Defects Mech Prop 43:201

    CAS  Google Scholar 

  11. Sansoz F, Molinari JF (2005) Acta Mater 53(7):1931

    Article  CAS  Google Scholar 

  12. Dorfman S, Fuks D, Malbouisson LAC, et al (2003) Computational Mater Sci 27(1–2):199

    Article  CAS  Google Scholar 

  13. Chandra N, Dang P (1999) J Mater Sci 34(4):655

    Article  CAS  Google Scholar 

  14. Bishop GH Jr, Harrison R, Kwok T, Yip S (1982) J Appl Phys 53:5596

    Article  CAS  Google Scholar 

  15. King TAH, Smith DA (1980) Acta Crystallogr A 36:335

    Article  CAS  Google Scholar 

  16. Wang GJ, Sutton AP, Vitek V (1984) Acta Metallurgica 32(7):1093

    Article  CAS  Google Scholar 

  17. Hyde B, Farkas D (2005) Philos Mag 85(32):3795

    Article  CAS  Google Scholar 

  18. Geng WT, Freeman AJ, Wu R, Geller CB, Raynolds JE (1999) Phys Rev B 60:7149

    Article  CAS  Google Scholar 

  19. Ballo P, Degmova J, Slugen V (2005) Phys Rev B 72(6)

  20. Simonelli G, Pasianot R, Savino EJ (1993) Mater Res Soc 291:567

    Article  CAS  Google Scholar 

  21. Ruda M, Farkas D, Abriata J (2002) Scr Materialia 46(5):349

    Article  CAS  Google Scholar 

  22. Ruda M, Farkas D, Abriata J (1996) Phy Rev B 54(14):9765

    Article  CAS  Google Scholar 

  23. Campbell GH, Kumar M, King WE, et al (2002) Philos Mag A – Phy Cond Matter Struct Defects Mech Prop 82(8):1573

    CAS  Google Scholar 

  24. Latapie A, Farkas D (2003) Scr Materialia 48(5):611

    Article  CAS  Google Scholar 

  25. Chang JP, Bulatov VV, Yip S (1999) J Computer – Aided Mater Design 6(2–3):165

    Article  CAS  Google Scholar 

  26. Chang JP, Bulatov VV, et al (2001) MSE&A 309:160

    Article  Google Scholar 

  27. Cahn JW, Mishin Y, Suzuki A (2006) Philos Mag 86:3965

Download references

Acknowledgements

This work was supported by NSF, Materials Theory.

Author information

Authors and Affiliations

  1. Department of Materials Science and Engineering, Virginia Tech., 201 Holden, Blacksburg, VA, 24061, USA

    Joshua Monk, Brian Hyde & Diana Farkas

Authors
  1. Joshua Monk
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Brian Hyde
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Diana Farkas
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Diana Farkas.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Monk, J., Hyde, B. & Farkas, D. The role of partial grain boundary dislocations in grain boundary sliding and coupled grain boundary motion. J Mater Sci 41, 7741–7746 (2006). https://doi.org/10.1007/s10853-006-0552-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10853-006-0552-3

Keywords

Search

Navigation