Abstract
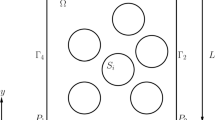
The quality of thermosetting polymer foams (like polyurethane foam, used for example in automotive industry) mainly depends on the manufacturing process. At a mesoscopic scale, the foam can be modelled by the expansion of gas bubbles in a polymer matrix with evolutionary rheological behaviour. The initial bubbles correspond to germs, which are supposed quasi-homogeneously distributed in the polymer. An elementary foam volume (∼1 mm3) is phenomenologically modelled by a diphasic medium (polymer and immiscible gas bubbles). The evolution of each component is governed by equations resulting from thermodynamics of irreversible processes: the relevant state variables in gas, resulting from chemical reaction creating carbon dioxide (assimilated then to a perfect gas), are pressure, temperature and conversion rate of the reaction. The number of gas moles in each bubble depends on this conversion rate. The foam is considered as a shear-thinning viscous fluid, whose rheological parameters evolve with the curing reaction, depending on the process conditions (temperature, pressure). A mixed finite element method with multidomain approach is developed to simulate the average growth rate of the foam during its manufacture and to characterize the influence of the manufacturing conditions (or initial rheological behaviour of the components) on macroscopic parameters of the foam (cell size, heterogeneity of porosity, wall thickness).
Similar content being viewed by others
References
L. Lefebvre and R. Keunings, Mathematical Modelling and Computer Simulation of the Flow of Chemically-Reacting Polymeric Foams, in “Mathematical Modelling for Materials Processing,” edited by M. Cross, J. F. T. Pittman, R. D. Wood, (Clarendon Press, Oxford, 1993) p 417.
G. Oertel, in “Polyurethane Handbook” (Hanser Publishers, Munich, 1985).
D. Weaire and S. Hutzler, “The Physics of Foams” (Oxford University Press, Oxford, 1999).
E. Mora, L. D. Artavia and C. W. Macosko, Modulus development during reactive polyurethane foaming, J. Rheol. 35 (1991) 921.
S. L. Everitt, O. G. Harlen, H. J. Wilson and D. J. Read, Bubble dynamics in viscoelastic fluids with application to reacting and non-reacting polymer foams, J. Non Newt. Fluid Mech. 114 (2003) 83.
P. Perzyna, Fundamental problems in viscoelasticity, Adv Appl. Mech. 9 (1966) 243.
M. Amon and D. C. Denson, A study of the dynamics of foam growth: analysis of the growth of closely spaced spherical bubbles, Polym. Eng. Sci. 24 (1984) 1026.
M. I. Aranguren and R. J. J. Williams, Kinetic and statistical aspects of the formation of polyurethanes from toluene diisocyanate, Polymer 27 (1986) 425.
J. Bikard, T. Coupez and B. Vergnes, Modèlisation numérique multidomaines de l’expansion réactive d’une mousse polymère par création de gaz, Actes du 38ème Colloque du Groupe Français de Rhéologie, CD ROM (2003), Brest, France.
G. O. Piloyan, I. D. Ryabchikov and O. S. Novikora, Determination of activation energies of chemical reactions by differential thermal analysis, Nature, 5067 (1966) 1229.
R. B. Kellog and B. Liu, A finite element method for the compressible Navier-Stokes equations. SIAM J. Num. Anal., 33 (1996) 788.
D. N. Arnold, F. Brezzi and M. Fortin, A stable finite element for Stokes equations. Calcolo 21 (1984) 344.
S. Batkam, J. Bruchon and T. Coupez, A space-time discontinuous Galerkin method for convection and diffusion in injection moulding. Intern. J. Form. Proc. 7 (2003) 11.
E. Pichelin and T. Coupez, Finite element solution of the 3D mold filling problem for viscous incompressible fluid. Comput. Meth. Appl. Mech. Eng. 163 (1999) 371.
E. Bigot and T. Coupez, Capture of 3D moving free surfaces and material interfaces by mesh deformation. in Proceedings ECCOMAS 2000, Barcelona, CD Rom (2000).
J. Bruchon and T. Coupez, Étude 3D de la formation d'une structure de mousse polymère par simulation de l'expansion anisotherme de bulles de gaz, Mécanique & Industries 4 (4)(2003) pp. 331.
Z. H. Tu, V. P. W. Shim and C. T. Lim, Plastic deformation modes in rigid polyurethane foam under static loading, Int. J. Solids Struct., 38 (2001) 9267.
J. M. Castro and C. W. Macosko, Kinetics and rheology of typical polyurethane reaction injection molding systems, SPE ANTEC Tech. Papers (1980) 434.
F. Dimier, N. Sbirrazzuoli, B. Vergnes and M. Vincent, Curing kinetics and chemorheological analysis of polyurethane formation, Polym. Eng. Sci., 44 (2004) 518.
G. A. Campbell, Polyurethane foam process development. A systems engineering approach. J. Appl. Polym. Sci. 16 (1972) 1387.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Bikard, J., Bruchon, J., Coupez, T. et al. Numerical prediction of the foam structure of polymeric materials by direct 3D simulation of their expansion by chemical reaction based on a multidomain method. J Mater Sci 40, 5875–5881 (2005). https://doi.org/10.1007/s10853-005-5022-9
Received:
Accepted:
Issue Date:
DOI: https://doi.org/10.1007/s10853-005-5022-9