Abstract
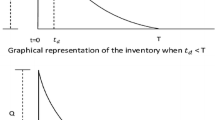
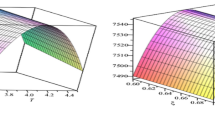
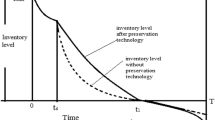
This research analyzes the impact of deploying suitable preservation technology for an inventory system in which units are subject to constant rate of deterioration. The demand is considered to be function of time and retail price. It is assumed that the supplier offers a fixed credit period to the retailer and retailer also offers credit period to the customers. The goal is to maximize the total profit per unit time with respect to optimal investment to be made in preservation technology, retail price of an item and purchase quantity. The concavity of the total profit is validated using numerical example. The managerial issues are discussed.
Similar content being viewed by others
References
Goyal, S.K.: Economic order quantity under conditions of permissible delay in payments. J. Oper. Res. Soc. 36(4), 335–338 (1985)
Shah, N.H., Soni, H.N., Jaggi, C.K.: Inventory model and trade credit: review. Control. Cybern. 39(3), 867–884 (2010)
Huang, Y.F.: Optimal retailer’s ordering policies in the EOQ model under trade credit financing. J. Oper. Res. Soc. 54, 1011–1015 (2003)
Huang, Y.F.: An inventory model under two levels of trade credit and limited storage space derived without derivatives. Appl. Math. Model. 30, 418–436 (2006)
Huang, Y.F.: Optimal retailer’s replenishment decisions in the EPQ model under two levels of trade credit policy. Eur. J. Oper. Res. 176, 1577–1591 (2007)
Teng, J.T., Chang, C.T.: Optimal manufacturer’s replenishment policies in the EPQ model under two-levels of trade credit policy. Eur. J. Oper. Res. 195, 358–363 (2009)
Wee, H.M.: Economic production lot size model for deteriorating items with partial back ordering. Comput. Ind. Eng. 24, 449–458 (1993)
Raafat, F.: Survey of literature on continuously deteriorating inventory models. J. Oper. Res. Soc. 40, 27–37 (1991)
Shah, N.H., Shah, Y.K.: Literature survey on inventory models for deteriorating items. Econ. Ann. 44, 221–237 (2000)
Goyal, S.K., Giri, B.C.: Recent trend in modeling of deteriorating inventory. Eur. J. Oper. Res. Soc. 134, 1–16 (2001)
Bakker, M., Riezebos, J., Teunter, R.H.: Review of inventory systems with deterioration since 2001. Eur. J. Oper. Res. 221, 125–138 (2012)
Lee, H.H.: The investment model in prevention maintenance in multi-level production systems. Int. J. Prod. Econ. 112, 816–828 (2008)
Hsu, P.H., Wee, H.M., Teng, H.M.: Preservation technology investment for deteriorating inventory. Int. J. Prod. Econ. 124, 338–394 (2010)
Uckun, C., Karaesmen, F., Savas, S.: Investment in improved inventory accuracy in a decentralized supply chain. Int. J. Prod. Econ. 113, 546–566 (2008)
Dye, C.Y., Hsieh, T.P.: An optimal replenishment policy for deteriorating items with effective investment in preservation technology. Eur. J. Oper. Res. 218, 106–112 (2012)
He, Y., Huang, H.: Two-level credit financing for noninstantaneous deterioration items in a supply chain with downstream credit-linked demand. Discret. Dyn. Nat. Soc. Article ID 917958, p 22. doi:10.1155/2013/917958 (2013)
Hsieh, T.P., Dye, C.Y.: A production inventory model incorporating the effect of preservation technology investment when demand is fluctuating with time. J. Comput. Appl. Math. 239, 25–36 (2013)
Teng, J.T., Goyal, S.K.: Optimal ordering policies for a retailer in a supply chain with up-stream and down-stream trade credits. J. Oper. Res. Soc. 58, 1252–1255 (2007)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Shah, N.H., Shah, D.B. & Patel, D.G. Optimal Preservation Technology Investment, Retail Price and Ordering Policies for Deteriorating Items under Trended Demand and Two Level Trade Credit Financing. J Math Model Algor 14, 1–12 (2015). https://doi.org/10.1007/s10852-014-9253-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10852-014-9253-0