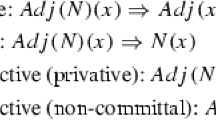Abstract
The paper introduces a proof-theoretic semantics (PTS) for adjectival modification (adjective–noun combination) as an alternative to the traditional model-theoretic semantics basing meaning on truth-conditions. The paper considers the proof-theoretic meaning of modification by means of the three traditional adjective classes: intersective, subsective and privative. It does so by introducing a meaning-conferring natural-deduction proof system for such modification. The PTS theory of meaning is not polluted by ontological commitments, for example, a scale for beauty and a yardstick for being beautiful. It only uses syntactic artefacts of the proof language. The paper also defines, by suitable rules, iterated modification, shedding light on the relationship between iteration and adjectival classes. Modification via coordinated adjectives is covered too. An appendix delineates briefly the main ingredients of PTS.

Similar content being viewed by others
Notes
All NL examples are displayed in the San Serif font and are always mentioned, never used.
In general, any nominal grammatical function can serve this purpose, as in Francez and Dyckhoff (2010a); the restriction here to subjects only is merely for simplicity.
Not to be confused with context of utterance.
The exact nature of this collection depends on the structural rules assumed.
As is common in ND-presentation, in actual examples we suppress the \(\Gamma \), using only the succedent, to save space; note that \(\Gamma \) is easily recoverable in such small examples.
I follow Morzycki (2015) in reserving ‘subsective’ to adjectives which are subsective but not intersective adjectives.
For example, if negation is taken as classical, a fake fake gun is a gun, a non-obvious and controversial entailment.
That is, there is no explicit sign in the formula expressing the product.
Obviously, assuming that every adjective parameterizes over every noun is an over-idealisation. However, a finer, more restricted parameterization is obviously imposable, and I skip further details here.
I ignore here a pragmatic effect of an intensification of the modification by repeating the adjective, as in

like a use of very.
Another reading of such sentences, producing a different parameterisation, is presented in Sect. 5.
This is known as Gentzen’s ‘logistic’ presentation of ND.
This possibility was suggested to me by Andreas Fjellstad (p.c.).
References
Bankston, P. (2003). Modelling nonintersective adjectives using operator logics. Review of Modern Logic, 9(1–2), 9–28.
Francez, N. (2014a). Harmony in multiple-conclusions natural-deduction. Logica Universalis, 8(2), 215–259. doi:10.1007/s11787-014-0103-7.
Francez, N. (2014b). A proof-theoretic semantics for contextual domain restriction. Journal of Language modelling, 2(2), 249–283.
Francez, N. (2014c). Views of proof-theoretic semantics: Reified proof-theoretic meanings. Journal of Computational Logic. Special issue in honour of Roy Dyckhoff. doi:10.1093/logcom/exu035.
Francez, N. (2015a). On distinguishing proof-theoretic consequence from derivability. Logique et Analysis (to appear).
Francez, N. (2015b). On semi-fusions and semi-negations. South American Journal of Logic (SAJL) (accepted).
Francez, N. (2015c). On the notion of canonical derivations from open assumptions and its role in proof-theoretic semantics. Review of Symbolic Logic, 8(2), 296–305. doi:10.1017/S1755020315000027.
Francez, N. (2015d). Proof-theoretic semantics. London: College Publications.
Francez, N., & Ben-Avi, G. (2015). A proof-theoretic reconstruction of generalized quantifiers. Journal of Semantics, 32(3), 313–371. doi:10.1093/jos/ffu001.
Francez, N., & Ben-Avi, G. (2011). Proof-theoretic semantic values for logical operators. Review of Symbolic Logic, 4(3), 337–485.
Francez, N., & Dyckhoff, R. (2010). Proof-theoretic semantics for a natural language fragment. Linguistics and Philosophy, 33(6), 447–477.
Francez, N., Dyckhoff, R., & Ben-Avi, G. (2010). Proof-theoretic semantics for subsentential phrases. Studia Logica, 94, 381–401.
Francez, N., & Wieckowski, B. (2014). A proof-theoretic semantics for contextual definiteness. In E. Moriconi & L. Tesconi (Eds.), Second Pisa colloquium in logic, language and epistemology. Pisa: ETS.
Morzycki, M. (2015). Modification., Key topics in semantics and pragmatics series. Cambridge: Cambridge University Press.
Paoli, F. (1999). Comparative logic as an approach to comparison in natural language. Journal of Semantics, 16, 67–96.
Acknowledgements
I thank Itamar Francez and Chris Kennedy for various discussions and clarifications about the topics of the paper. I thank Ivo Pezlar for spotting and correcting some errors in an earlier version of the manuscript.
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
In this appendix, I repeat for self-containment of the paper some of the technicalities involved in PTS in general. A detailed presentation of PTS as a theory of meaning is presented in Francez (2015d), with the second part of that book devoted to the application of PTS to NL. Further references are provided in that book. Motivation and justification for PTS can be found also in Francez and Dyckhoff (2010a), Francez and Ben-Avi (2015e).
According to the PTS programme, meaning is determined by a meaning-conferring natural-deduction proof system. Such a system has two kinds of rules:
-
Introduction rules (I -rules) Those rules have as their conclusion an expression (formula, sentence) governed by an operator said to be introduced by the rule. Such rules establish the way the expression can be deduced from the premises of the rule. Such an inference is considered the most direct way to infer the conclusion. In the natural language fragment considered in this paper, I-rules introduce a \(\textit{dp}\) as a subject of an intransitive verb, and introduce implicit operators combining adjectives and nouns.
-
Elimination rules (E -rules) Those rule have as their major premise an expression (formula, sentence) governed by an operator said to be eliminated by the rule. Such rules establish the way a conclusion may be drawn from that expression. Such an inference is considered the most direct way to infer from the major premise. In the natural language fragment considered in this paper, an E-rules eliminate a \(\textit{dp}\) from the subject position of an intransitive verb, as well as the implicit operator combining adjectives and verbs.
Both kind of rules may discharge assumptions when applied, rendering the conclusion independent of some temporarily assumed assumptions.
Example 6.1
The simplest example of I/E-rules are those introducing and eliminating a (sentential) conjunction in logic, shown below.

Note that there are two E-rules here. No discharge of assumption is involved in those rules.
The claim of PTS is, that those rules determine the full meaning of conjunction, independently of the model-theoretic definition using truth-tables.
Example 6.2
A simple example involving a discharge of an assumption is the I-rule of the implication.

The rule (\(\rightarrow I\)) says that in order to derive an implication, temporary assume the antecedent \(\varphi \), putting around it square brackets to indicate discharge, indexed i for connecting with a discharging application of the rule indexed by the same index, and derive the consequent \(\psi \), potentially using the assumption of the antecedent. Once the consequent has been derived, the assumption of the antecedent is discharged. The E-rule is the familiar modus-ponens.
Once again, according to PTS, those rules tell “the whole story” needed for the meaning of implication.
OfficiallyFootnote 12, the I/E-rules are formulated using sequents of the form \(\Gamma \vdash \psi \), where \(\Gamma \) is a finite collection (most often, a set) of object-language formulas, the undischarged assumptions, and \(\psi \) is also a formula. In this presentation, the dependence of a conclusion on assumption is made explicit. However, to avoid notational cluttering, The assumptions \(\Gamma \) are left implicit. A derivation \(\mathcal{D}\) (of \(\psi \) from \(\Gamma \)) is defined recursively by iterating rule applications starting from assumptions \(\Gamma \) and reaching a conclusion \(\psi \). The derivability (i.e., existence of a derivation) of \(\varphi \) from \(\Gamma \) in \(\mathcal{N}\) is denoted \(\vdash _{\mathcal{N}} \Gamma : \varphi \) (where the subscript on ‘\(\vdash \)’ is often omitted). A variable is called fresh if it does not occur in any assumption of which a conclusion of a rule depends.
In the PTS literature, meaning is conceived as implicitly defined by the I-rules, not appealing to any proof-theoretic semantic value as an explicit definition. But what exactly can be taken as an explicitly defined proof-theoretic semantic value within PTS as the result of the determination of meaning via the meaning-conferring I-rules?
In Francez and Ben-Avi (September 2011), and subsequently in Francez (2014c), such a proof-theoretic semantic value is proposed as an explicit definition of meaning. I recapitulate this proposal below.
An important concept in PTS, on which the definition of explicit meaning definition is based, is that of a canonical derivation in \(\mathcal{N}\). Following Francez (2014a, 2015c), I suggest the following definition, generalizing the standard canonical proof (from no assumptions). Its justification is discussed in detail in Francez (2015c).
Definition 6.1
(canonical derivation from open assumptions). A \(\mathcal{N}\)-derivation \(\mathcal{D}\) for \(\Gamma \vdash \psi \) (for a compound \(\psi \)) is canonical iff it satisfies one of the following two conditions.
-
The last rule applied in \(\mathcal{D}\) is an I-rule (for the main operator of \(\psi \)).
-
The last rule applied in \(\mathcal{D}\) is an assumption-discharging E-rule, the major premise of which is some \(\varphi \) in \(\Gamma \), and its encompassed sub-derivations \(\mathcal{D}_{1},\ldots ,\mathcal{D}_{n}\) are all canonical derivations of \(\psi \).
Denote by \(\vdash _{\mathcal{N}}^{c}\) canonical derivability in \(\mathcal{N}\), and by \(\mathbf{[}\! [\varphi \mathbf{] \! ]}^{c}_{\Gamma }\) the (possibly empty) collection of canonical derivations of \(\varphi \) from \(\Gamma \).
For \(\Gamma \) empty, the definition reduces to that of a canonical proof. Note the recursion involved in this definition. The important observation regarding this recursion is that it always terminates via the first clause, namely by an application of an I-rule. I refer to this application of an I-rule as the essential application, the outcome of which is propagated throughout the canonical derivation.
There are no canonical derivations for an atomic sentence, which by definition has no introducible operators. Traditionally, the PTS programme views the meaning of an atomic sentence to be given, possibly from outside the meaning-conferring proof system. To overcome this non-specificity, I takeFootnote 13 the rule of assumption \(\vdash \Gamma , p : p\) to constitute the canonical way an atomic sentence is introduced into a derivation.
To realize the role of canonicity in the forthcoming definition of reified proof-theoretic meanings, consider the following example derivation in, say, intuitionistic propositional logic.

This is a derivation of a conjunction—but not a canonical one, as it does not end with an application of \((\wedge I)\), nor does it have an essential application of it. Thus, the conjunction here was not derived according to its meaning! As far as this derivation is concerned, it could mean anything, e.g., disjunction. On the other hand, the following example derivation is according to the conjunction’s meaning, being canonical.

I now turn to the definition of what I take to be the reified proof-theoretic meaning determined by a meaning-conferring \(\textit{ND}\)-system (see Francez (2014c) for a more detailed discussion).
I take the sentential meanings of compound sentences in L to originate from canonical \(\mathcal{N}\)-derivations. I emphasize once again, that it is sentential meanings that are directly explicitly defined by the \(\textit{ND}\)-system, whereas meanings of connectives are extracted from compound sentential meanings as shown in Francez et al. (2010b). I refer to functions from contexts to collections of \(\textit{ND}\)-derivations as contextualized functions.
Definition 6.2
(meaning—sentential semantic values). For \(\varphi \in L\), its meaning \(\mathbf{[}\! [\varphi \mathbf{] \! ]}\), is given as follows.
Note that the reified meaning of \(\varphi \) is a proof-theoretic object, a contextualized function from contexts to the collection of canonical derivations of \(\varphi \) from that context, not to be confused with model-theoretic denotations (of truth-values, in the propositional logic case).
The definition of proof-theoretic consequence (pt-consequence) rests on the notion of grounds for assertion for \(\varphi \), closely related to \(\mathbf{[}\! [\varphi \mathbf{] \! ]}\), the reified meaning of \(\varphi \).
Definition 6.3
(grounds for assertion).
Thus, any \(\Gamma \) that canonically derives \(\varphi \) serves as grounds for assertion of \(\varphi \).
Based on the definitions of grounds for assertion, I define proof-theoretic consequence (pt-consequence).
Definition 6.4
(proof-theoretic consequences). Let \(\Gamma ,\psi \in L\). \(\psi \) is a proof-theoretic consequence of \(\Gamma \) (\(\Gamma \Vdash \psi \)) iff \(GA \mathbf{[}\! [\Gamma \mathbf{] \! ]}\subseteq GA \mathbf{[}\! [\psi \mathbf{] \! ]}\).
Thus, pt-consequences is based on grounds propagation: every grounds for asserting \(\psi \) (that derives canonically \(\psi \)), are already collective grounds for collectively asserting all of \(\Gamma \) [depending on the mode of combination of grounds employed, see Francez (2015a)].
By this definition, \(\psi \) is a pt-consequence of \(\Gamma \) according to \(\psi \)’s meaning as pt-consequence involves canonical derivability.
I want to stress that according to the PTS programme, the rules proposed are meaning-conferring. That is, they are a definitional tool. They should not be judged against any external yard-stick, in particular not one used in MTS. Completeness proofs as traditionally sought in logic are not a goal here, in spite of being an interesting topic on its own. The rules need, though, meet some proof-theoretic criteria to qualify as meaning-conferring. In Francez and Dyckhoff (2010a), the rules for the extensional fragment are shown to meet the harmony criterion, one central such criterion.
Rights and permissions
About this article
Cite this article
Francez, N. A Proof-Theoretic Semantics for Adjectival Modification. J of Log Lang and Inf 26, 21–43 (2017). https://doi.org/10.1007/s10849-016-9245-8
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10849-016-9245-8