Skip to main content
SpringerLink
Log in

Spatial Modeling and Robust Flight Control Based on Adaptive Sliding Mode Approach for a Quadrotor MAV

  • Published:
Journal of Intelligent & Robotic Systems Aims and scope Submit manuscript

Abstract

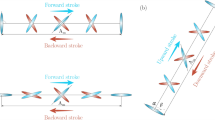
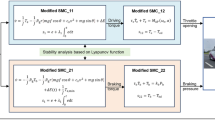
This paper addresses the design of a robust flight control for a quadrotor micro aerial vehicle under external perturbations. The spatial vectors convention is implemented in order to represent the mathematical model of the system. Then, a flight control based on an adaptive second order sliding mode technique is designed. This controller allows to mitigate matched and bounded perturbations/uncertainties with unknown bounds, while non overstimating of the control gain; its adaptive gains permit to reduce the control effort as well as the chattering effect. Furthermore, a closed loop analysis under perturbations is given. Simulation results include a comparison between the proposed adaptive flight control against a second order sliding mode approach showing the feasibility and attractiveness of strategy.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Cai, G., Dias, J., Seneviratne, L.: A survey of small-scale unmanned aerial vehicles: recent advances and future development trends. Unmanned Syst. 2(2), 175–199 (2014)

    Article  Google Scholar 

  2. Mohd, M.A., Husain, A.R., Danapalasingam, K.A.: Enhanced backstepping controller design with application to autonomous quadrotor unmanned aerial vehicle. J. Intell. Robot. Syst. 79(2), 295–321 (2015)

    Article  Google Scholar 

  3. Dydek, Z.T., Annaswamy, A.M., Lavretsky, E.: Adaptive control of quadrotor UAVs: a design trade study with flight evaluations. IEEE Trans. Control Syst. Technol. 21(4), 1400–1406 (2013)

    Article  Google Scholar 

  4. Satici, A.C., Poonawala, H., Spong, M.W.: Robust optimal control of quadrotor UAVs. IEEE Access 1 (1), 79–93 (2013)

    Article  Google Scholar 

  5. Gautam, D., Ha, C.: Control of a quadrotor using a smart self-tuning fuzzy PID controller. Int. J. Adv. Robot. Syst. 10(11), 1–9 (2013)

    Article  Google Scholar 

  6. Xiong, J., Zhang, G.: Global fast dynamical terminal sliding mode control for a quadrotor UAV. ISA Transactions. (2016). https://doi.org/10.1016/j.isatra.2016.09.019

  7. Xiong, J., Zheng, E.: Position and attitude tracking control for a quadrotor UAV. ISA Trans. 53, 725–731 (2014)

    Article  Google Scholar 

  8. Zheng, E., Xiong, J., Luo, J.: Second order sliding mode control for a quadrotor UAV. ISA Trans. 53, 1350–1356 (2014)

    Article  Google Scholar 

  9. Besnard, L., Shtessel, Y., Landrum, B.: Quadrotor vehicle control via sliding mode controller driven by sliding mode disturbance observer. J. Frankl. Inst. 349, 658–684 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  10. Luque-Vega, L., Castillo-Toledo, B., Loukianov, A.: Robust block second order sliding mode control for a quadrotor. J. Frankl. Inst. 349, 719–739 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  11. Rida, M., Cherki, B.: A new robust control for minirotorcraft unmanned aerial vehicles. ISA Trans. 56, 86–101 (2014)

    Google Scholar 

  12. Ramirez, H., Parra, V., Sanchez, A., Garcia, O.: Robust backstepping control based on integral sliding modes for tracking of quadrotors. J. Intell. Robot. Syst. 73, 51–66 (2014)

    Article  Google Scholar 

  13. Sumantri, B., Uchiyama, N., Sano, S.: Generalized super-twisting sliding mode control with a nonlinear sliding surface for robust and energy-efficient controller of a quad-rotor helicopter. Proc. Inst. Mech. Eng. C J. Mech. Eng. Sci. (2016). https://doi.org/10.1177/0954406216628897

  14. Villanueva, A., Castillo-Toledo, B., et al.: System for a Quadrotor (2015)

  15. Derafa, L., Benallegue, A., Fridman, L.: Super twisting control algorithm for the attitude tracking of a four rotors UAV. J. Frankl. Inst. 349, 685–689 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  16. Ibarra, E., Castillo, P.: Nonlinear super twisting algoritmh for UAV attitude stabilization (2017)

  17. Castañeda, H., Gordillo, J.L.: Spatial modeling, identification and adaptive second order sliding mode control of a micro air vehicle. In: 2017 International Conference on Unmanned Aircraft Systems (ICUAS) Miami, FL, USA, June 13–16 (2017)

  18. Phang, S.K., Li, K., Yu, K.H., et al.: Systematic design and implementation of a micro unmanned quadrotor system. Unmanned Syst. 2(2), 121–141 (2014)

    Article  Google Scholar 

  19. Mellinger, D., Michael, N., Kumar, V.: Trajectory generation and control for precise aggressive maneuvers with quadrotors. Int. J. Robot. Res. 31(5), 664–674 (2012)

    Article  Google Scholar 

  20. Moreno, J., Osorio, M.: Strict Lyapunov Functions for the Super-Twisting Algorithm. IEEE Trans. Autom. Control 57(4), 1035–1040 (2012)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgments

This paper was a short version of the one presented in ICUAS 2017. Additionally, this work was part of a Postdoctoral stay at the Robotics National Laboratory of the ITESM-CONACyT.

Author information

Authors and Affiliations

  1. Tecnologico de Monterrey, Escuela de Ingenieria y Ciencias, Ave. Eugenio Garza Sada 2501, Monterrey, N.L., 64849, México

    Herman Castañeda & J. L. Gordillo

Authors
  1. Herman Castañeda
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. J. L. Gordillo
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Herman Castañeda.

Additional information

Publisher’s Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Castañeda, H., Gordillo, J.L. Spatial Modeling and Robust Flight Control Based on Adaptive Sliding Mode Approach for a Quadrotor MAV. J Intell Robot Syst 93, 101–111 (2019). https://doi.org/10.1007/s10846-018-0819-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10846-018-0819-3

Keywords

Search

Navigation