Abstract
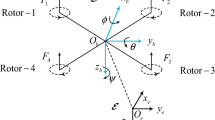
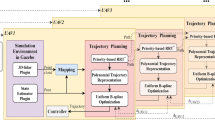
This paper presents a novel concurrent optimal trajectory planning method for a team of quadrotors to switch between various formation patterns in the confined indoor environment. Using static shape-based, dynamic trajectory-based approaches, different formation patterns of quadrotors can be optimally and rapidly arranged and localized. The modified algorithm of optimal reciprocal collision avoidance (ORCA) is applied to produce the nominal collision-free trajectories for the quadrotor team as the first stage, which is extended to three-dimensional space and the downwash effect induced by the propellers is effectively addressed. Considering the flatness property of the quadrotor dynamics, the jerk-optimized trajectories based on the cubic clamped B-spline are then generated and these corresponding constraints are also satisfied. Moreover, a robust perfect tracking (RPT) outer-loop controller is designed to compensate the poor resolution of the indoor localization system. Finally, simulations are conducted to verify these proposed algorithms, and the real-world flight result was successfully showcased at the opening ceremony of Rotorcraft Asia & Unmanned Systems Asia 2017.
Similar content being viewed by others
References
Agha-mohammadi, A.-a., Ure, N.K., How, J.P., Vian. J.: Health aware stochastic planning for persistent package delivery missions using quadrotors. In: IEEE /RSJ International Conference on Intelligent Robots and Systems, pp. 3389–3396. Chicago (2014)
Alvissalim, M.S., Zaman, B., Hafizh, Z.A., Ma’sum, M.A., Jati, G., Jatmiko, W., Mursanto, P.: Swarm quadrotor robots for telecommunication network coverage area expansion in disaster area. In: Annual Conference of the Society of Instrument and Control Engineers of Japan, pp. 2256–2261. Akita (2012)
Augugliaro, F., Schoellig, A.P., D’Andrea, R.: Methods for designing and executing an aerial dance choreography. IEEE Robot. Autom. Mag. 20(4), 96–104 (2013)
Basri, M.A.M., Husain, A.R., Danapalasingam, K.A.: Enhanced backstepping controller design with application to autonomous quadrotor unmanned aerial vehicle. J. Intell. Robot. Syst. 79(2), 295–321 (2015)
Chen, B.M., Lee, T.H., Peng, K.M., Venkataramanan, V.: Hard Disk Drive Servo Systems, 2nd edn. Springer, London (2006)
De Boor, C.: A Practical Guide to Splines, vol. 27. Springer-Verlag, New York (1978)
Du, Q., Faber, V., Gunzburger, M.: Centroidal Voronoi Tessellations: Applications and Algorithms. SIAM Rev. 41(4), 637–676 (1999)
Egerstedt, M., Hu, X., Stotsky, A.: Control of mobile platforms using a airtual vehicle approach. IEEE Trans. Autom. Control 46(11), 1777–1782 (2001)
Elbanhawi, M., Simic, M., Jazar, R.N.: Continuous path smoothing for car-like robots using b-spline curves. J. Intell. Robot. Syst. 80(1), 23–56 (2015)
Fiorini, P, Shiller, Z.: Motion planning in dynamic environments using velocity obstacles. Int. J. Robot. Res. 17(7), 760–772 (1998)
Guadarrama-Olvera, J.R., Corona-Sánchez, J.J., Rodriguez-Cortes, H.: Hard real-time implementation of a nonlinear controller for the quadrotor helicopter. J. Intell. Robot. Syst. 73(1-4), 81–97 (2014)
Guérin, F., Guinand, F., Brethé, J.F., Pelvillain, H., et al.: Towards an autonomous warehouse inventory scheme. In: IEEE Symposium Series on Computational Intelligence, pp. 1–8, Athens (2016)
Guo, K., Qiu, Z., Miao, C., Zaini, A.H., Chen, C.L., Meng, W., Xie, L.: Ultra-wideband-based localization for quadcopter navigation. Unmanned Syst. 4(01), 23–34 (2016)
Hehn, M., D’Andrea, R.: Real-time trajectory generation for quadrocopters. IEEE Trans. Robot. 31(4), 877–892 (2015)
Kano, H., Nakata, H., Martin, C.F.: Optimal curve fitting and smoothing using normalized uniform b-splines: a tool for studying complex systems. Appl. Math. Comput. 169(1), 96–128 (2005)
Kano, H., Fujioka, H., Martin, C.F.: Optimal smoothing and interpolating splines with constraints. Appl. Math. Comput. 218(5), 1831–1844 (2011)
Kumar, V., Michael, N.: Opportunities and challenges with autonomous micro aerial vehicles. In: Robotics Research, pp. 41–58. Springer (2017)
Kuriki, Y., Namerikawa, T.: Consensus-based cooperative formation control with collision avoidance for a multi-UAV system. In: American Control Conference, pp. 2077–2082. Portland (2014)
Mellinger, D., Kumar, V.: Minimum snap trajectory generation and control for quadrotors. In: IEEE International Conference on Robotics and Automation, pp. 2520–2525. Shanghai (2011)
Mellinger, D., Kushleyev, A., Kumar, V.: Mixed-integer quadratic program trajectory generation for heterogeneous quadrotor teams. In: IEEE International Conference on Robotics and Automation, pp. 477–483. St Paul (2012)
Mücke, E.P., Saias, I., Zhu, B.: Fast randomized point location without preprocessing in two-and three-dimensional Delaunay triangulations. Comput. Geom. 12(1-2), 63–83 (1999)
Munkres, J.: Algorithms for the assignment and transportation problems. J. Soc. Indus. Appl. Math. 5(1), 32–38 (1957)
Rosales, C., Leica, P., Sarcinelli-Filho, M., Scaglia, G., Carelli, R.: 3D formation control of autonomous vehicles based on null-space. J. Intell. Robot. Syst. 84(1-4), 453–467 (2016)
Turpin, M., Michael, N., Kumar, V.: CAPT: concurrent assignment and planning of trajectories for multiple robots. Int. J. Robot. Res. 33(1), 98–112 (2014)
Van Den Berg, J., Guy, S.J., Lin, M., Manocha, D.: Reciprocal n-body collision avoidance. In: Robotics research, pp. 3–19. Springer (2011)
Wang, F., Liu, P., Zhao, S., Chen, B.M., Phang, S.K., Lai, S., Pang, T., Wang, B., Cai, C., Lee, T.H.: Development of an unmanned helicopter for vertical replenishment. Unmanned Syst. 3(01), 63–87 (2015)
Acknowledgements
This work was supported by National Natural Science Foundation of China [grant number 61673327], China Scholarship Council [grant number 201606310153], as well as Aviation Science Foundation of China [grant number 20160168001]. The authors would like to thank Prof. Ben M. Chen and his Unmanned System Research Group at National University of Singapore.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Foundation items: National Natural Science Foundation of China (61673327), China Scholarship Council (201606310153) and Aviation Science Foundation of China (20160168001).
Rights and permissions
About this article
Cite this article
Xu, Y., Lai, S., Li, J. et al. Concurrent Optimal Trajectory Planning for Indoor Quadrotor Formation Switching. J Intell Robot Syst 94, 503–520 (2019). https://doi.org/10.1007/s10846-018-0813-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10846-018-0813-9