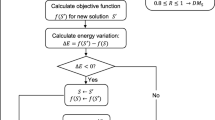
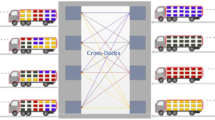
Abstract
Uncertainty and non-deterministic nature of the real world makes planning and scheduling in cross-docks a very complicated task for decision makers. These constant changes that happen all the time, often, lead to an increase in costs and/or a decrease in efficiency. Most of the uncertainty in cross-docks is caused by un-known truck arrival times. In this study we address the problem of scheduling incoming and outgoing trucks at a cross-dock facility, when vehicle arrival times are unknown, through a cost-stable scheduling strategy. Two meta-heuristics, MODE and NSGA-II, are used for solving the designed sample problems and are compared with a random search based genetic algorithm existing in the literature. Finally, performance of each algorithm is measured and analyzed using four metrics: quality, spacing, diversification and mean ideal distance. The results indicate that the proposed model MODE algorithm performs better in comparison with the other two methods.










Similar content being viewed by others
References
Altiparmak, F., Gen, M., Lin, L., & Karaoglan, I. (2009). A steady-state genetic algorithm for multi-product supply chain network design. Computers & Industrial Engineering, 56, 521–537.
Boloori Arabani, A., Zandieh, M., & Fatemi Ghomi, S. M. T. (2011a). A cross-docking scheduling problem with sub-population multi-objective algorithms. The International Journal of Advanced Manufacturing Technology, 58, 741761.
Boloori Arabani, A. R., Fatemi Ghomi, S. M. T., & Zandieh, M. (2011b). Meta-heuristics implementation for scheduling of trucks in a cross-docking system with temporary storage. Expert Systems with Applications, 38, 1964–1979.
Boysen, N. (2010). Truck scheduling at zero-inventory cross docking terminals. Computers & Operations Research, 37, 32–41.
Boysen, N., Briskorn, D., & Tschöke, M. (2012). Truck scheduling in cross-docking terminals with fixed outbound departures. OR Spectrum, 35, 479–504.
Boysen, N., & Fliedner, M. (2010). Cross dock scheduling: Classification, literature review and research agenda. Omega, 38, 413–422.
Chen, F., & Lee, C.-Y. (2009). Minimizing the makespan in a two-machine cross-docking flow shop problem. European Journal of Operational Research, 193, 59–72.
Chen, F., & Song, K. (2009). Minimizing makespan in two-stage hybrid cross docking scheduling problem. Computers & Operations Research, 36, 2066–2073.
Golias, M. M., Ivey, S., Haralambides, H., & Saharidis, G. (2010). Maximizing throughput and minimizing tardiness and earliness at a cross dock facility: A bi-objective formulation. Washington: Annual Meeting of the Transportation Research Board.
Hansen, P., Jaumard, B., & Savard, G. (1992). New branch-and-bound rules for linear bilevel programming. SIAM Journal on Scientific and Statistical Computing, 13, 1194–1217.
Konur, D., & Golias, M. M. (2013). Cost-stable truck scheduling at a cross-dock facility with unknown truck arrivals: A meta-heuristic approach. Transportation Research Part E: Logistics and Transportation Review, 49, 71–91.
Kuo, Y. (2013). Optimizing truck sequencing and truck dock assignment in a cross docking system. Expert Systems with Applications, 40, 5532–5541.
Liao, T. W., Egbelu, P. J., & Chang, P. C. (2013). Simultaneous dock assignment and sequencing of inbound trucks under a fixed outbound truckschedule in multi-door cross docking operations. International Journal of Production Economics, 141, 212–229.
Storn, R., & Price, K. (1997). Differential evolution—A simple and efficient heuristic for global optimization over continuous spaces. Journal of Global Optimization, 11, 341–359.
Tavakkoli-Moghaddam, R., Azarkish, M., & Sadeghnejad-Barkousaraie, A. (2010). Solving a multi-objective job shop scheduling problem with sequence-dependent setup times by a Pareto archive PSO combined with genetic operators and VNS. The International Journal of Advanced Manufacturing Technology, 53, 733750.
Van Belle, J., Valckenaers, P., & Cattrysse, D. (2012). Cross-docking: State of the art. Omega, 40, 827–846.
Wang, Z. X., Chan, F. T. S., Chung, S. H., & Niu, B. (2015). Minimization of delay and travel time of yard trucks in container terminals using an improved GA with guidance search. Mathematical Problems in Engineering, 2015, 1–12.
Wang, Z. X., Chan, F. T. S., Chung, S. H., & Niu, B. (2014). A decision support method for internal truck employment. Industrial Management and Data Systems, 114, 1378–1395.
Yu, W., & Egbelu, P. J. (2008). Scheduling of inbound and outbound trucks in cross docking systems with temporary storage. European Journal of Operational Research, 184, 377–396.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Heidari, F., Zegordi, S.H. & Tavakkoli-Moghaddam, R. Modeling truck scheduling problem at a cross-dock facility through a bi-objective bi-level optimization approach. J Intell Manuf 29, 1155–1170 (2018). https://doi.org/10.1007/s10845-015-1160-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10845-015-1160-3