Abstract
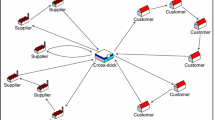
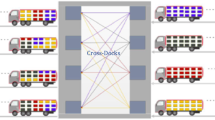
Cross docking play an indispensable role in streamlining the efficiency and effectiveness of any supply chain operations. Owing to the need to reduce transportation lead time and increase coordination between other supply chain activities such as just-in-time, make-to-order, or merge-in-transit strategies, shortening the total transfer time at cross docking is increasing important. Thus, in this paper we propose a new hybrid metaheuristic for vehicle routing scheduling in cross-docking systems. This new hybrid algorithm incorporates the elements from Particle Swam Optimization, Simulated Annealing and Variable Neighborhood Search to enhance its search capabilities. On view of the fact that the performance of metaheuristic algorithms are considerably influenced by the proper tuning of their parameters, we take advantage of Taguchi’s robust design method to come up with the best parameters of the before-mentioned algorithms. In order to measure the performance of our proposed algorithm, we compared it with the Tabu Search algorithm presented by Lee et al. (Comput Ind Eng 51:247–256, 2006). The computational evaluations clearly support the high performance of our proposed algorithm against other algorithm in the literature.
Similar content being viewed by others
References
Aarts E., Lenstra J. K. (1997) Search in combinatorial optimization. Wiley, New York
Ahuja R. K., Ergun O., Orlin J. B., Punnen A. P. (2002) A survey of very large-scale neighborhood search techniques. Discrete Apply Mathematics 123: 75–102
Apte M. U., Viswanathan S. (2000) Effective cross docking for improving distribution efficiencies. International Journal of Logistics: Research and Applications 3(3): 291–302
Barbarosoglu G., Ozgur D. (1999) A Tabu search algorithm for the vehicle routing problem. Computer & Operational Research 26: 255–270
Bartholdi J. J. III, Gue R. K. (2004) The best shape for a crossdock. Transportation Sciences 38(2): 235–244
Boysen, N., Fliedner, M., & Scholl, A. (2008). Scheduling inbound and outbound trucks at crossdocking terminals. OR Spectrum, 1–27.
Chen F., Song K. L. (2006) Cross docking logistics scheduling problem and its approximation and exact algorithms. Industry Engineering and Management 6: 53–58
Chen, F., & Song, K. L. (2008). Minimizing makespan in two-stage hybrid cross docking scheduling problem, Computers & Operations Research. doi:10.1016/j.cor.2008.07.003.
Dong, G., Tang, J., Lai, K. K., & Kong, Y. (2009). An exact algorithm for vehicle routing and scheduling problem of free pickup and delivery service in flight ticket sales companies based on set-partitioning model. Journal of Intelligent Manufacturing. doi:10.1007/s10845-009-0311-9.
Eddie Y. K., Ng E. W., Kee N. (2006) Parametric study of the biopotential equation for breast tumour identification using ANOVA and Taguchi method. International Federation for Medical and Biological Engineering 44: 131–139
Eiben A. E., Hinterding R., Michalewicz Z. (1999) Parameter control in evolutionary algorithms. IEEE Transactions on Evolutionary Computation 3(22): 124–141
Glover F. (1989) Tabu search. Part I. ORSA Journal on Computing 1: 190–206
Glover F. (1990) Tabu search. Part II. ORSA Journal on Computing 2: 4–32
Glover F., Laguna M. (1997) Tabu search. Kluwer, Boston
Grefenstette J. J. (1986) Optimisation of control parameters for genetic algorithms. IEEE Transaction on Systems, Man and Cybernetics 16(1): 122–128
Hansen P., Mladenovic N., Dragan U. (2004) Variable neighborhood search for the maximum clique. Discrete Applied Mathematics 145(1): 117–125
Janiak A., Kozan E., Lichtenstein M., Oguz C. (2007) Metaheuristic approaches to the hybrid flowshop scheduling problem with a cost-related criterion. International Journal of Production Economics 105: 407–424
Jia H. Z., Nee A. Y. C., Fuh J. Y. H., Zhang Y. F. (2003) A modified genetic algorithm for distributed scheduling. Journal of Intelligent Manufacturing 14: 3–4
Kennedy, J., & Eberhart, R. (1995). Particle swarm optimization. In Proceeding of the 1995 IEEE international conference on neural network, Perth, Australia, 1942–1948
Kirkpatrick S., Gelatt C. D., Vecchi M. P. (1983) Optimization by simulated annealing. Science 220: 671–680
Landrieu A., Mati Y., Binder Z. (2001) A tabu search heuristic for the single vehicle pickup and delivery problem with time windows. Journal of Intelligent Manufacturing 12: 5–6
Lau H. C., Sim M., Teo K. M. (2003) Vehicle routing problem with time windows and a limited number of vehicles. European Journal of Operational Research 148: 559–569
Lee Y. H., Jung W. J., Lee K. M. (2006) Vehicle routing scheduling for cross-docking in the supply chain. Computers & Industrial Engineering 51: 247–256
Li Y., Lim A., Rodrigues B. (2004) Crossdocking—JIT scheduling with time windows. Journal of the Operational Research Society 55(12): 1342–1351
Lim A., Ma H., Miao Z. et al (2006) Truck dock assignment problem with time windows and capacity constraint in transshipment network through crossdocks. In: Gavrilova M. (eds) Computational science and its applications—ICCSA. Springer, Berlin/Heidelberg, pp 688–697
Lim A., Ma H., Miao Z. (2006) Truck dock assignment problem with operational time constraint within crossdocks. In: Ali M., Dapoigny R. (eds) Advances in applied artificial intelligence. Springer, Berlin/Heidelberg, pp 262–271
Ma D. Y., Chen F. (2007) Dynamic programming algorithm on two machines cross docking scheduling. Journal of Shanghai Jiao Tong University 41(5): 852–856
Michalewicz Z. (1996) Genetic algorithms + data structures = evolution programs (3rd ed.). Springer, Berlin, Heidelberg, New York
Michalewicz Z., Schoenauer M. (1996) Evolutionary algorithms for constrained parameter optimisation problems. Evolutionary Computation 4(1): 1–32
Mosheiov G. (1998) Vehicle routing with pick-up and delivery: tour—partitioning heuristics. Computers & Industrial Engineering 34: 669–684
Rohrer, M. (1995). Simulation and cross docking. In Proceedings of the 1995 winter simulation conference (pp. 846–849).
Roshanaei V., Naderi B., Jolai F., Khalili M. (2009) A variable neighborhood search for job shop scheduling with setup times to minimize makespan. Future Generation Computer Systems 25: 654–661
Schwind G. F. (1996) A systems approach to docks and cross docking. Material Handling Engineering 51(2): 59–62
Tian P., Ma J., Zhang D. M. (1999) Application of the simulated annealing algorithm to the combinatorial optimization problem with permutation property: An investigation of generation mechanism. European Journal of Operational Research 118: 81–94
Vahdani, B., & Zandieh, M. (2009). Scheduling trucks in cross-docking systems: Robust meta-heuristics. Computers & Industrial Engineering. doi:10.1016/j.cie.2009.06.006.
Waller M. A., Richard C. C., Ozment J. (2006) Impact of cross-docking on inventory in a decentralized retail supply chain. Transportation Research Part E 42: 359–382
Wang, C. H., & Lu, J. Z. (2009). An effective evolutionary algorithm for the practical capacitated vehicle routing problems. Journal of Intelligent Manufacturing. doi:10.1007/s10845-008-0185-2.
Wang J. F., Regan A. (2008) Real-time trailer scheduling for cross dock operations. Transportation Journal 47(2): 5–20
Yao X. (1995) A new simulated annealing algorithm. International Journal of Computer Mathematics 56: 161–168
Yu W., Egbelu P. J. (2008) Scheduling of inbound and outbound trucks in cross docking systems with temporary storage. European Journal of Operational Research 184: 377–396
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Vahdani, B., Tavakkoli-Moghaddam, R., Zandieh, M. et al. Vehicle routing scheduling using an enhanced hybrid optimization approach. J Intell Manuf 23, 759–774 (2012). https://doi.org/10.1007/s10845-010-0427-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10845-010-0427-y