Skip to main content
SpringerLink
Log in

Improvement of RF MEMS devices by spring constant scaling laws

  • Published:
Journal of Computational Electronics Aims and scope Submit manuscript

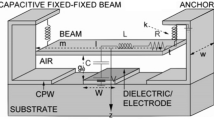
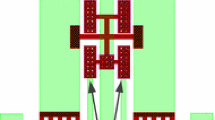
Abstract

The technology for radio frequency micro-electro-mechanical system (RF MEMS) is well established. In the next phase of miniaturization, RF MEMS transforming into RF nano-electro-mechanical system (NEMS) requires scaling laws. For MEMS devices, vertical scaling laws are available in the literature. However, existing scaling laws are isotropic and not valid for the majority of the MEMS devices. Like VLSI technology, the scaling in the MEMS is asymmetric and needs optimization in each direction. In the MEMS, depending upon the working principle, the scaling laws vary from device to device. In the present work, spring constant scaling laws for the electrostatic RF MEMS devices are derived given the device performance. The scaling laws are derived in such a way that existing limitations of the MEMS technology like low switching speed, high pull-in voltage, stiction, etc., are minimized and the response of the switch is improved.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

References

  1. De Groot, W.A., Webster, J.R., Felnhofer, D., Gusev, E.P.: Review of device and reliability physics of dielectrics in electrostatically driven MEMS devices. IEEE Trans. Device Mater. Reliab. 9(2), 190–202 (2009). https://doi.org/10.1109/TDMR.2009.2020565

    Article  Google Scholar 

  2. Zaghloul, U., Piazza, G.: Highly scalable NEMS relays with stress-tuned switching voltage using piezoelectric buckling actuators. IEEE Trans. Electron Devices 61(10), 3520–3528 (2014). https://doi.org/10.1109/TED.2014.2331914

    Article  Google Scholar 

  3. Wautelet, M.: Scaling laws in the macro, micro and nanoworlds. Eur. J. Phys. 22(6), 601–611 (2001). https://doi.org/10.1088/0143-0807/22/6/305

    Article  Google Scholar 

  4. Trimmer, W.S.N.: Microrobots and micromechanical systems. Sensors and Actuators 19(3), 267–287 (1989). https://doi.org/10.1016/0250-6874(89)87079-9

    Article  Google Scholar 

  5. Bansal, D., Bajpai, A., Kumar, P., Kaur, M., Kumar, A.: Effect of Stress on Pull-in Voltage of RF MEMS SPDT Switch. IEEE Trans. Electron Devices 67(5), 2147–2152 (2020). https://doi.org/10.1109/ted.2020.2982667

    Article  Google Scholar 

  6. Bansal, D., Bajpai, A., Mehta, K., Kumar, P., Kumar, A.: Improved Design of Ohmic RF MEMS Switch for Reduced Fabrication Steps. IEEE Trans. Electron Devices 66(10), 4361–4366 (2019). https://doi.org/10.1109/TED.2019.2932846

    Article  Google Scholar 

  7. Bansal, D., Kumar, A., Sharma, A., Kumar, P., Rangra, K.J.: Design of novel compact anti-stiction and low insertion loss RF MEMS switch. Microsyst. Technol. 20(2), 337–340 (2013). https://doi.org/10.1007/s00542-013-1812-1

    Article  Google Scholar 

  8. Rangra, K., et al.: Symmetric toggle switch—a new type of rf MEMS switch for telecommunication applications: Design and fabrication. Sensors Actuators A Phys. 123–124, 505–514 (2005). https://doi.org/10.1016/j.sna.2005.03.035

    Article  Google Scholar 

  9. Jindal, S.K., Magam, S.P., Shaklya, M.: Analytical modeling and simulation of MEMS piezoresistive pressure sensors with a square silicon carbide diaphragm as the primary sensing element under different loading conditions. J. Comput. Electron. 17(4), 1780–1789 (2018). https://doi.org/10.1007/s10825-018-1223-8

    Article  Google Scholar 

  10. Varma, M.A., Jindal, S.K.: Novel design for performance enhancement of a touch-mode capacitive pressure sensor: theoretical modeling and numerical simulation. J. Comput. Electron. 17(3), 1324–1333 (2018). https://doi.org/10.1007/s10825-018-1174-0

    Article  Google Scholar 

  11. Pu, S.H., Holmes, A.S., Yeatman, E.M., Papavassiliou, C., Lucyszyn, S.: Stable zipping RF MEMS varactors. J. Micromechanics Microengineering 20(3), 035030 (2010). https://doi.org/10.1088/0960-1317/20/3/035030

    Article  Google Scholar 

  12. Rebeiz, G.M.: RF MEMS: Theory, Design, and Technology. John Wiley & Sons Inc, Hoboken, NJ, USA (2003)

    Book  Google Scholar 

  13. He, X., et al.: Design and consideration of wafer level micropackaging for distributed RF MEMS phase shifters. Microsyst. Technol. 14(4–5), 575–579 (2007). https://doi.org/10.1007/s00542-007-0438-6

    Article  Google Scholar 

  14. S. Gong, H. Shen, and N. S. Barker (2011) “A 60-GHz 2-bit switched-line phase shifter using SP4T RF-MEMS switches.” IEEE Trans Microw Theory Tech. 59(4); 894–900. doi: https://doi.org/10.1109/TMTT.2011.2112374.

  15. Bansal, D., Bajpai, A., Kumar, P., Kumar, A., Kaur, M., Rangra, K.: Design and fabrication of a reduced stiction radio frequency MEMS switch. J. Micro/Nanolithography, MEMS, MOEMS 14(3), 035002 (2015). https://doi.org/10.1117/1.JMM.14.3.035002

    Article  Google Scholar 

  16. Van Spengen, W.M., Puers, R., De Wolf, I.: On the physics of stiction and its impact on the reliability of microstructures. J. Adhes. Sci. Technol. 17(4), 563–582 (2003). https://doi.org/10.1163/15685610360554410

    Article  Google Scholar 

  17. a Koszewski, F. Souchon, C. Dieppedale, D. Bloch, and T. Ouisse (2013) “Physical model of dielectric charging in MEMS.” J. Micromechanics Microengineering. 23(4); 045019. doi: https://doi.org/10.1088/0960-1317/23/4/045019.

  18. Tas, N., Sonnenberg, T., Jansen, H., Legtenberg, R., Elwenspoek, M.: Stiction in surface micromachining. J. Micromechanics Microengineering 6(4), 385–397 (1996). https://doi.org/10.1088/0960-1317/6/4/005

    Article  Google Scholar 

  19. S. Melle et al (2007) “Investigation of Stiction Effect in Electrostatic Actuated RF MEMS Devices.” in 2007 Topical Meeting on Silicon Monolithic Integrated Circuits in RF Systems. 21(2); 173–176, doi: https://doi.org/10.1109/SMIC.2007.322787.

Download references

Author information

Authors and Affiliations

  1. CSIR-Central Electronics Engineering Research Institute, Pilani, 333031, Rajasthan, India

    Deepak Bansal, Prem Kumar & Amit Kumar

Authors
  1. Deepak Bansal
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Prem Kumar
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Amit Kumar
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Deepak Bansal.

Ethics declarations

Conflict of interest

Authors declare no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Bansal, D., Kumar, P. & Kumar, A. Improvement of RF MEMS devices by spring constant scaling laws. J Comput Electron 20, 1006–1011 (2021). https://doi.org/10.1007/s10825-021-01657-z

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10825-021-01657-z

Keywords

Search

Navigation