A full-range dual material gate tunnel field effect transistor drain current model considering both source and drain depletion region band-to-band tunneling

Abstract

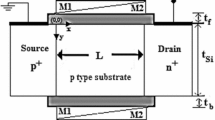
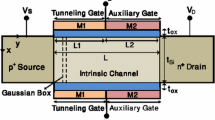
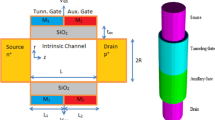
In this paper, a 2-D analytical model for the drain current of a dual material gate tunneling field-effect transistor is developed incorporating the effects of source and drain depletion regions. The model can forecast the effects of drain voltage, gate work function, oxide thickness, and silicon film thickness. The proposed model gives analytical expressions for the surface potential, electric field and the band to band generation rate which is numerically integrated to give the drain current. More importantly, our model accurately predicts the ambipolar current and the effects of drain voltage in the saturation region. A semi-empirical approach is used to model the transition from the linear to the saturation region, leading to an infinitely differentiable characteristics. The model is shown to be scalable down to a gate length of 50 nm. The model validation is carried out by a comparison with 2-D numerical simulations.

Appendix

The coefficients $\hbox {a}_{1}$ and $\hbox {b}_{1}$ for the source depletion region (R1) are found by applying the boundary conditions as given in (16) and solving the resultant six linear equations in the six variables $\hbox {a}_{\mathrm{i}}$ and $\hbox {b}_{\mathrm{i}}$:

$$\begin{aligned} a_{1}&= e^{-k_{2}L_{2}-k_{3}L_{3}}\nonumber \\&\quad \times \left( { \begin{array}{l} e^{k_{1}L_{1}}\left( {\Psi _{source} -\psi _{c1}}\right) \left( { \begin{array}{l} \Delta k_{23} (\Delta k_{12} e^{2k_{3}L_{3}}-\Sigma k_{12} e^{2k_{2}L_{2}}) \\ +\Sigma k_{23} (\Sigma k_{12} e^{2k_{2}L_{2}+2k_{3}L_{3}}-\Delta k_{12} ) \\ \end{array}} \right) \\ +\,k_{2}\Delta \psi _{1,2t} \left( { \begin{array}{l} \Delta k_{32} (e^{2k_{2}L_{2}}+e^{2k_{3}L_{3}}) \\ +\Sigma k_{32} (1+e^{2k_{2}L_{2}+2k_{3}L_{3}} \\ \end{array}} \right) \\ +\,k_{2}e^{k_{2}L_{2t}}\Delta \psi _{2a,2t} \left( { \begin{array}{l} \Delta k_{23} (e^{2k_{2}L_{2a}}+e^{2k_{3}L_{3}}) \\ -\Sigma k_{23} (1+e^{2k_{2}L_{2a} +2k_{3}L_{3}}) \\ \end{array}} \right) \\ +\,2k_{2}k_{3}e^{k_{2}L_{2}}\Delta \psi _{2a,3} (1+e^{2k_{3}L_{3}})+4(\Psi _{drain} -\psi _{c3} )e^{k_{2}L_{2}+2k_{3}L_{3}} \\ \end{array}} \right) \nonumber \\ b_{1}&= \Psi _{source} -\psi _{c1} -a_{1}. \end{aligned}$$

(19)

Here additional symbols $\Delta \psi _{i,j}$, $\Delta k_{ij}$ and $\Sigma k_{ij}$ have been defined for compact representation of the coefficients $\hbox {a}_{1}$ and $\hbox {b}_{1}$:

$$\begin{aligned}&\Delta \psi _{i,j} =\psi _{ci} -\psi _{cj} \nonumber \\&\Delta k_{ij} = k_{i}-k_{j}\nonumber \\&\Sigma k_{ij} = k_{i}+k_{j} \end{aligned}$$

(20)