Abstract
We present a formalization of convex polyhedra in the proof assistant Coq. The cornerstone of our work is a complete implementation of the simplex method, together with the proof of its correctness and termination. This allows us to define the basic predicates over polyhedra in an effective way (i.e. as programs), and relate them with the corresponding usual logical counterparts. To this end, we make an extensive use of the Boolean reflection methodology.The benefit of this approach is that we can easily derive the proof of several fundamental results on polyhedra, such as Farkas’ Lemma, the duality theorem of linear programming, and Minkowski’s Theorem.


Similar content being viewed by others
Notes
It can be downloaded by executing
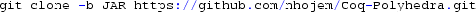 . Instructions for building can be found in the README.md file.
. Instructions for building can be found in the README.md file.The double index in
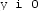 and
and
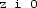 comes from the fact that column vectors are encoded as matrices (with one column).
comes from the fact that column vectors are encoded as matrices (with one column).When such a d exists, the value of the objective function of \(\mathrm {DualLP}(A,b,0)\) can be made arbitrarily large by considering points of the form \(\alpha d\), for \(\alpha \ge 0\), which obviously belong to \(\mathcal {Q}(A,0)\) (due to the latter property, d is called a dual feasible direction, see Sect. 5.2).
The command
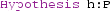 is synonymous to the command
is synonymous to the command
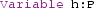 that is used for local declarations when
that is used for local declarations when
 is an identifier and
is an identifier and
 is a proposition. This means that h is a proof term of
is a proposition. This means that h is a proof term of
 . The hypothesis is then added to list of hypotheses (or, equivalently, of variables) of the subsequent statements.
. The hypothesis is then added to list of hypotheses (or, equivalently, of variables) of the subsequent statements.We make a slight abuse of language, since feasibility usually applies to linear programs, or systems of contraints. By extension, we apply it to polyhedra: \(\mathcal {P}(A,b)\) is feasible if it is nonempty.
If
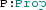 and
and
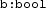 , the statement
, the statement
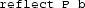 means that either
means that either
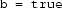 and P, or
and P, or
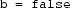 and
and
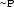 hold. We refer to [14] for an introduction on the way Boolean reflection is used in MathComp.
hold. We refer to [14] for an introduction on the way Boolean reflection is used in MathComp.
References
Armand, M., Faure, G., Grégoire, B., Keller, C., Théry, L., Werner, B.: A modular integration of sat/smt solvers to coq through proof witnesses. In: Jouannaud, J.P., Shao, Z. (eds.) Certified Programs and Proofs, pp. 135–150. Springer Berlin Heidelberg, Berlin (2011)
Avis, D.: A revised implementation of the reverse search vertex enumeration algorithm. In: Kalai, G., Ziegler, G.M. (eds.) Polytopes—Combinatorics and Computation. Birkhäuser, Basel (2002). https://doi.org/10.1007/978-3-0348-8438-9_9
Avis, D., Fukuda, K.: A pivoting algorithm for convex hulls and vertex enumeration of arrangements and polyhedra. Discrete Comput. Geom. 8(3), 295–313 (1992). https://doi.org/10.1007/BF02293050
Barthe, G., Forest, J., Pichardie, D., Rusu, V.: Defining and reasoning about recursive functions: a practical tool for the Coq proof assistant. In: Hagiya, M., Wadler, P. (eds.) Proceedings of FLOPS 2006. Springer Berlin Heidelberg, Berlin (2006). https://doi.org/10.1007/11737414_9
Besson, F.: Fast reflexive arithmetic tactics the linear case and beyond. In: Altenkirch, T., McBride, C. (eds.) Proceedings of TYPES 2006. Springer, Berlin (2007). https://doi.org/10.1007/978-3-540-74464-1_4
Böhme, S., Weber, T.: Fast lcf-style proof reconstruction for z3. In: Kaufmann, M., Paulson, L.C. (eds.) Interactive Theorem Proving, pp. 179–194. Springer Berlin Heidelberg, Berlin (2010)
Bremner, D., Deza, A., Hua, W., Schewe, L.: More bounds on the diameters of convex polytopes. Optim. Methods Softw. 28(3), 442–450 (2013). https://doi.org/10.1080/10556788.2012.668906
Cohen, C., Dénès, M., Mörtberg, A.: Refinements for free!. In: Gonthier, G., Norrish, M. (eds.) Proceedings of CPP 2013. Springer, pp. 84–96. Berlin (2013). https://doi.org/10.1007/978-3-319-03545-1_10
Cousot, P., Halbwachs, N.: Automatic discovery of linear restraints among variables of a program. In: Proceedings of POPL 1978, pp. 84–96. ACM Press, Tucson (1978)
Dantzig, G.B.: Maximization of a linear function of variables subject to linear inequalities. In: Activity Analysis of Production and Allocation. Wiley, New York (1951)
Dantzig, G.B., Orden, A., Wolfe, P.: The generalized simplex method for minimizing a linear form under linear inequality restraints. Pac. J. Math. 5(2), 183–195 (1955)
Fouilhe, A., Boulmé, S.: A certifying frontend for (sub) polyhedral abstract domains. In: Giannakopoulou, D., Kroening, D. (eds.) Proceedings of VSTTE 2014. Springer, Berlin (2014). https://doi.org/10.1007/978-3-319-12154-3_13
Gonthier, G.: Point-free, set-free concrete linear algebra. In: van Eekelen, M., Geuvers, H., Schmaltz, J., Wiedijk, F. (eds.) Proceedings of ITP 2011. Springer, Berlin (2011). https://doi.org/10.1007/978-3-642-22863-6_10
Gonthier, G., Mahboubi, A., Tassi, E.: A Small Scale Reflection Extension for the Coq system. Research Report RR-6455, Inria Saclay Ile de France (2016)
Guglielmi, N., Laglia, L., Protasov, V.: Polytope Lyapunov functions for stable and for stabilizable LSS. Found. Comput. Math. 17(2), 567–623 (2017). https://doi.org/10.1007/s10208-015-9301-9
Harrison, J.: The HOL light theory of Euclidean space. J. Autom. Reason. 50, 173–190 (2013)
Joswig, M., Loho, G., Lorenz, B., Schröter, B.: Linear programs and convex hulls over fields of puiseux fractions. In: Kotsireas, I.S., Rump, S.M., Yap, C.K. (eds.) Mathematical Aspects of Computer and Information Sciences, pp. 429–445. Springer, Cham (2016)
Khachiyan, L.: Polynomial algorithms in linear programming. USSR Comput. Math. Math. Phys. 20(1), 53–72 (1980). https://doi.org/10.1016/0041-5553(80)90061-0
Matschke, B., Santos, F., Weibel, C.: The width of five-dimensional prismatoids. Proc. Lond. Math. Soc. 110(3), 647–672 (2015). https://doi.org/10.1112/plms/pdu064
Obua, S.: Proving bounds for real linear programs in isabelle/hol. In: Hurd, J., Melham, T. (eds.) Theorem Proving in Higher Order Logics, pp. 227–244. Springer Berlin Heidelberg, Berlin (2005)
Sakaguchi, K.: Vass. https://github.com/pi8027/vass (2016). Accessed 2 Aug 2018
Santos, F.: A counterexample to the Hirsch conjecture. Ann. Math. 176(1), 383–412 (2012). https://doi.org/10.4007/annals.2012.176.1.7
Schrijver, A.: Theory of Linear and Integer Programming. Wiley, New York (1986)
Smale, S.: Mathematical problems for the next century. Math. Intell. 20, 7–15 (1998)
Spasić, M., Marić, F.: Formalization of incremental simplex algorithm by stepwise refinement. In: Giannakopoulou, D., Méry, D. (eds.) Proceedings of FM 2012. Springer, Berlin (2012). https://doi.org/10.1007/978-3-642-32759-9_35
Acknowledgements
The authors are very grateful to A. Mahboubi for her help to improve the presentation of this paper, and to G. Gonthier, F. Hivert and P.-Y. Strub for fruitful discussions. The second author is also grateful to M. Cristiá for introducing him to the topic of automated theorem proving. The authors thank the anonymous reviewers for their suggestions and remarks. An abridged version of this work appeared in the proceedings of ITP’17. The authors finally thank the referees of the ITP paper for their comments and suggestions.
Author information
Authors and Affiliations
Corresponding author
Additional information
The authors were partially supported by the programme “Ingénierie Numérique & Sécurité” of ANR, project “MALTHY”, No. ANR-13-INSE-0003, by a public grant as part of the Investissement d’avenir project, reference ANR-11-LABX-0056-LMH, LabEx LMH and by the PGMO program of EDF and FMJH.
Rights and permissions
About this article
Cite this article
Allamigeon, X., Katz, R.D. A Formalization of Convex Polyhedra Based on the Simplex Method. J Autom Reasoning 63, 323–345 (2019). https://doi.org/10.1007/s10817-018-9477-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10817-018-9477-1





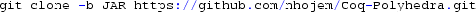 . Instructions for building can be found in the
. Instructions for building can be found in the 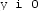 and
and
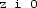 comes from the fact that column vectors are encoded as matrices (with one column).
comes from the fact that column vectors are encoded as matrices (with one column).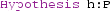 is synonymous to the command
is synonymous to the command
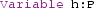 that is used for local declarations when
that is used for local declarations when
 is an identifier and
is an identifier and
 is a proposition. This means that h is a proof term of
is a proposition. This means that h is a proof term of
 . The hypothesis is then added to list of hypotheses (or, equivalently, of variables) of the subsequent statements.
. The hypothesis is then added to list of hypotheses (or, equivalently, of variables) of the subsequent statements.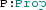 and
and
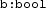 , the statement
, the statement
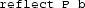 means that either
means that either
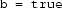 and P, or
and P, or
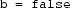 and
and
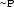 hold. We refer to [
hold. We refer to [