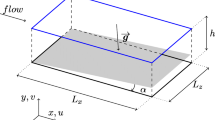
Abstract
The fluid dynamic environment within a photobioreactor is critical for performance as it controls mass transfer of photosynthetic gases (CO2 and O2) and the mixing environment of the algal culture. At a cellular level, light fluctuation will occur when cells move between the “light”, well-illuminated volume of the culture near the light source and the “dark”, self-shaded zone of the culture. Controlled light/dark frequency may increase the light to biomass yield and prevent photoinhibition. Knowledge of cell trajectories within the reactor is therefore important to optimize culture performance. This study examines the cell trajectories and light/dark frequencies in a stratified gas–liquid flow tubular photobioreactor. Commercially available computational fluid dynamics software, ANSYS Fluent, was used to investigate cell trajectories within the half-full solar receivers at different liquid velocities and reactor tube diameters. In the standard configuration 96-mm solar receiver tube, the light/dark cycle frequencies ranged from 0.104 to 0.612 Hz over the liquid velocity range of 0.1 to 1 m s−1. In comparison, the smaller diameter 48- and 24-mm tubes exhibit higher light/dark frequencies, 0.219 to 1.30 Hz and 0.486 to 2.67 Hz, respectively.









Similar content being viewed by others
Abbreviations
- CFD:
-
Computational fluid dynamics
- L/D:
-
light/dark
References
Borowitzka MA, Moheimani NR (2011) Sustainable biofuels from algae. Mitig Adapt Strateg Glob Change. doi:10.1007/s11027-010-9271-9
Carvalho AP, Meireles LA, Malcata FX (2006) Microalgal reactors: a review of enclosed system designs and performances. Biotechnol Prog 22:1490–506
Carvalho AP, Silva SO, Baptista JM, Malcata FX (2011) Light requirements in microalgal photobioreactors: an overview of biophotonic aspects. Appl Microbiol Biotechnol 89:1275–88
Degen J, Uebele A, Retze A, Schmid-Staiger U, Trösch W (2001) A novel airlift photobioreactor with baffles for improved light utilization through the flashing light effect. J Biotechnol 92:89–94
Eriksen N (2008) The technology of microalgal culturing. Biotechnol Lett 30:1525–36
Grobbelaar JU, Nedbal L, Tichý L (1996) Influence of high frequency light/dark fluctuations on photosynthetic characteristics of microalgae photoacclimated to different light intensities and implications for mass algal cultivation. J Appl Phycol 8:335–43
Janssen M, Janssen M, de Winter M, Tramper J, Mur LR, Snel J, Wijffels RH (2000) Efficiency of light utilization of Chlamydomonas reinhardtii under medium-duration light/dark cycles. J Biotechnol 78:123–37
Luo H-P, Al-Dahhan MH (2004) Analyzing and modeling of photobioreactors by combining first principles of physiology and hydrodynamics. Biotechnol Bioeng 85:382–93
Luo H-P, Al-Dahhan MH (2011) Verification and validation of CFD simulations for local flow dynamics in a draft tube airlift bioreactor. Chem Eng Sci 66:907–23
Luo H-P, Kemoun A, Al-Dahhan MH, Fernández Sevilla JM, García Sánchez JL, García Camacho F, Molina Grima E (2003) Analysis of photobioreactors for culturing high-value microalgae and cyanobacteria via an advanced diagnostic technique: CARPT. Chem Eng Sci 58:2519–27
Masojídek J, Kopecký J, Giannelli L, Torzillo G (2011) Productivity correlated to photobiochemical performance of Chlorella mass cultures grown outdoors in thin-layer cascades. J Ind Microbiol Biotechnol 38:307–17
Merchuk JC, Ronen M, Giris S, Arad S (1998) Light/dark cycles in the growth of the red microalga Porphyridium sp. Biotechnol Bioeng 59:705–13
Merchuk JC, Rosenblat Y, Berzin I (2007) Fluid flow and mass transfer in a counter-current gas–liquid inclined tubes photo-bioreactor. Chem Eng Sci 62:7414–25
Moberg AK, Ellem G, Jameson GJ, Herbertson J (2009) Mass transfer of photosynthetic gases within a multiphase microalgal production system. In conference proceedings of Chemeca 2009: Engineering Our Future: Are We Up to the Challenge?, Perth, Australia. Engineers Australia, Barton, pp 425–436. ISBN: 9780858259225
Moberg AK, Ellem G, Jameson GJ, Herbertson J. (2010) Fluid dynamical considerations in the design of a microalgae photobioreactor. In conference proceedings of Chemeca 2010: Engineering at the Edge, Adelaide, Australia. Engineers Australia, Barton, pp 421–431. ISBN: 9780858259713
Molina Grima E, Acién Fernández FG, García Camacho F, Chisti Y (1999) Photobioreactors: light regime, mass transfer, and scaleup. J Biotechnol 70:231–47
Perner-Nochta I, Posten C (2007) Simulations of light intensity variation in photobioreactors. J Biotechnol 131:276–85
Posten C (2009) Design principles of photo-bioreactors for cultivation of microalgae. Eng Life Sci 9:165–77
Pruvost J, Legrand J, Legentilhomme P, Muller-Feuga A (2002) Lagrangian trajectory model for turbulent swirling flow in an annular cell: comparison with residence time distribution measurements. Chem Eng Sci 57:1205–15
Pruvost J, Cornet JF, Legrand J (2008) Hydrodynamics influence on light conversion in photobioreactors: an energetically consistent analysis. Chem Eng Sci 63:3679–94
Pulz O (2001) Photobioreactors: production systems for phototrophic microorganisms. Appl Microbiol Biotechnol 57:287–93
Pulz O, Gross W (2004) Valuable products from biotechnology of microalgae. Appl Microbiol Biotechnol 65:635–48
Richmond AE (1986) Microalgaculture. CRC Crit Rev Biotechnol 4:369–428
Richmond A (1996) Efficient utilization of high irradiance for production of photoautotrophic cell mass: a survey. J Appl Phycol 8:381–387
Richmond A, Cheng-Wu Z, Zarmi Y (2003) Efficient use of strong light for high photosynthetic productivity: interrelationships between the optical path, the optimal population density and cell-growth inhibition. Biomol Eng 20:229–36
Schenk P, Thomas-Hall S, Stephens E, Marx U, Mussgnug J, Posten C, Kruse O, Hankamer B (2008) Second generation biofuels: high-efficiency microalgae for biodiesel production. BioEnerg Res 1:20–43
Wu X, Merchuk JC (2002) Simulation of algae growth in a bench-scale bubble column reactor. Biotechnol Bioeng 80:156–68
Wu X, Merchuk JC (2004) Simulation of algae growth in a bench scale internal loop airlift reactor. Chem Eng Sci 59:2899–912
Wu LB, Li Z, Song YZ (2010) Hydrodynamic conditions in designed spiral photobioreactors. Bioresource Technol 101:298–303
Acknowledgments
This work is part of a PhD project investigating the process engineering fundamentals of microalgae production. The project is supported by the industry partner, The Crucible Group Pty Ltd, The Tom Farrell Institute for the Environment, and The University of Newcastle, Australia.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Moberg, A.K., Ellem, G.K., Jameson, G.J. et al. Simulated cell trajectories in a stratified gas–liquid flow tubular photobioreactor. J Appl Phycol 24, 357–363 (2012). https://doi.org/10.1007/s10811-011-9765-1
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10811-011-9765-1