Abstract
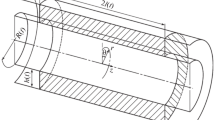
An analytical solution is found for the problem modeling quasistatic compression and flow of an ideal rigid plastic (under the Mises-Hencky criterion) material along the generatrix in a thin cylindrical layer. This problem is a generalization of the classical Prandtl problem. The small asymptotic parameter is the ratio of the layer thickness to its length. The radii of the cylinders can have any intermediate order of smallness. It is shown that when the radii and thickness of the layer are of the same order of smallness, the solution is asymptotically exact in the sense that the number of terms of the series describing the kinematic and dynamic parameters of the flow is finite. Limiting transitions to the classical Prandtl solution are investigated.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
L. Prandtl, “Anwendungsbeispiele zu einem Henckyschen Satzüber das plastische Gleichgewicht,” ZAMM, 4, No. 6, 401–406 (1923).
H. Geiringer and W. Prager, “Mechanik isotroper Körper im plastischen Zustand,” Ergeb. Exakten Naturwis, 13, 310–363 (1934).
A. A. Ils’yushin, “Complete plasticity in the flow between rigid surfaces: An analogy to a sand fill and some applications,” Prikl. Mat. Mekh., 19, No. 6, 693–713 (1955).
V. V. Sokolovskii, Theory of Plasticity [in Russian], Vysshaya Shkola, Moscow (1969).
B. D. Annin, V. O. Bytev, and S. I. Senashov, Group Properties of Elastic and Plastic Equations [in Russian], Nauka, Novosibirsk (1985).
B. A. Druyanov and R. I. Nepershin, Theory of Technological Plasticity [in Russian], Mashinostroenie, Moscow (1990).
M. A. Zadoyan, Dimensional Problems of Plasticity [in Russian], Nauka, Moscow (1992).
B. E. Pobedrya and I. L. Guzei, “Mathematical modeling of deformation of composites taking into account thermal diffusion,” Mat. Model. Sist. Prots., No. 6, 82–91 (1998).
A. Yu. Ishlinskii and D. D. Ivlev, Mathematical Theory of Plasticity [in Russian], Fizmatlit, Moscow (2001).
V. L. Kolmogorov, Plastic Working of Materials [in Russian], Ural. Gos. Tekh. Univ. (Ural. Polytech. Inst.), Ekaterinburg (2001).
I. A. Kiiko and V. A. Kadymov, “Generalization of the Prandtl problem of slab compression,” Vestn. Mosk. Gos. Univ., Ser. 1: Mat. Mekh., No. 4, 50–56 (2003).
S. E. Aleksandrov and E. A. Lyamina, “Strain-rate intensity factors in compression of a layer of a plastic material between cylindrical surfaces,” J. Appl. Mech. Tech. Phys., 50, No. 3, 504–511 (2009).
D. V. Georgievskii, “On an axisymmetric analog of the Prandtl problem,” Dokl. Ross. Akad. Nauk, 422, No. 3, 331–333 (2008).
D. V. Georgievskii, “Asymptotic expansions and the possibility of rejection of hypotheses in the Prandtl problem,” Izv. Ross. Akad. Nauk, Ser. Mekh. Tverd. Tela, No. 1, 83–93 (2009).
D. V. Georgievskii, “On ideal rigid flow of an asymptotically thin cylindrical layer,” Dokl. Ross. Akad. Nauk, 429, No. 3, 328–331 (2009).
Author information
Authors and Affiliations
Corresponding author
Additional information
Translated from Prik-ladnaya Mekhanika i Tekhnicheskaya Fizika, Vol. 51, No. 5, pp. 111–119, September–October, 2010
Rights and permissions
About this article
Cite this article
Georgievskii, D.V. Asymptotic Analysis of Plastic Flow along the Generatrix in a Thin Cylindrical Layer. J Appl Mech Tech Phy 51, 713–720 (2010). https://doi.org/10.1007/s10808-010-0091-1
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10808-010-0091-1