Abstract
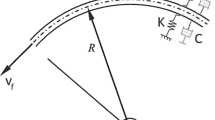
A model that describes propagation of the conversion front in a generalized plane stress state typical for technological conditions of coating synthesis on a substrate, with allowance for the coupled character of heat transfer and deformation without external mechanical loading, is proposed. A stationary solution is obtained in the approximation of a narrow combustion front. Ranges of model parameters where the temperature of reaction products and the components of stress and strain tensors behave differently are identified.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
L. D. Landau and E. M. Lifshits, Course of Theoretical Physics, Vol. 6: Fluid Mechanics, Pergamon Press, Oxford-Elmsford, New York (1987).
A. G. Merzhanov and B. I. Khaikin, Theory of Combustion Waves in Homogeneous Media [in Russian], Inst. of Struct. Macrokinetics, Russian Acad. of Sci., Chernogolovka (1992).
I. L. Pobol’, “Processing of structural and industrial materials and obtaining articles under the electron beam action,” Doct. Dissertation in Tech. Sci., Minsk (2007).
A. G. Knyazeva, “Effect of rheological properties of the medium on ignition and combustion characteristics,” in: Unsteady Combustion and Interior Ballistics, Proc. Int. Workshop (Saint Petersburg, June 26–30, 2001), Vol. 1, Baltic State Tech. Univ., St. Petersburg (2001), pp. 30–40.
A. G. Knyazeva, “The stationary modes of the reaction front and their stability for solid media with regard to chemically induced internal stresses and strains,” in: Combustion of Energetic Materials, Select. Papers of the 5th Int. Symp. on Special Topics in Chemical Propulsion (Stresa, Italy, June 18–22, 2000), Kluwer Acad. Publ., S. 1. (2001), pp. 867–878.
B. V. Novozhilov, “Propagation velocity of the exothermic reaction front in the condensed phase,” Dokl. Akad. Nauk SSSR, 141, No. 1, 151–153 (1961).
M. G. Makhviladze and B. V. Novozhilov, “Two-dimensional stability of the combustion of condensed systems,” J. Appl. Mech. Tech. Phys., 12, No. 5, 676–682 (1971).
K. G. Shkadinskii and B. I. Khaikin, “Effect of heat losses on propagation of the exothermal reaction front in the k-phase,” in: Combustion and Explosion [in Russian], Nauka, Moscow (1972), pp. 104–109.
A. G. Knyazeva, “Solution of the thermoelasticity problem in the form of a traveling wave and its application to analysis of possible regimes of solid-phase transformations,” J. Appl. Mech. Tech. Phys., 44, No. 2, 164–173 (2003).
Yu. A. Gordopolov, V. S. Trofimov, and A. G. Merzhanov, “Possibility of gasless detonation of condensed systems,” Dokl. Ross. Akad. Nauk, Fizika, 341, No. 3, 327–329 (1995).
S. S. Batsanov and Yu. A. Gordopolov, “Limits of solid-phase detonation velocity,” Dokl. Ross. Akad. Nauk, 341, No. 3, 327–329 (195).
L. G. Bolkhovitinov and S. S. Batsanov, “Theory of solid-state detonation,” Combust., Expl., Shock Waves, 43, No. 2, 219–221 (2007).
A. G. Knyazeva, “Combustion wave propagation through deformed solids,” Combust., Expl., Shock Waves, 29, No. 3, 299–303 (1993).
B. Boley and J. Weiner, Theory of Thermal Stresses, John Wiley and Sons, New York (1960).
A. G. Knyazeva, “Thermomechanical stability of the reaction front in the technology conditions,” in: Proc. 4th Europ. Combustion Meeting (Vienna, April 14–17, 2009), Vienna Univ. of Technol., Vienna (2009); CD ROM, P811400.
A. G. Knyazeva, “Velocity of the solid-phase combustion wave. Asymptotical analysis,” Fiz. Mezomekh., 7, No. 3, 63–70 (2004).
Author information
Authors and Affiliations
Corresponding author
Additional information
Translated from Prikladnaya Mekhanika i Tekhnicheskaya Fizika, Vol. 51, No. 2, pp. 27–38, March–April, 2010.
Rights and permissions
About this article
Cite this article
Knyazeva, A.G. Solid-phase combustion in a plane stress state. 1. Stationary combustion wave. J Appl Mech Tech Phy 51, 164–173 (2010). https://doi.org/10.1007/s10808-010-0025-y
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10808-010-0025-y