Abstract
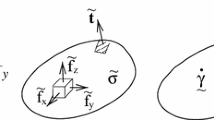
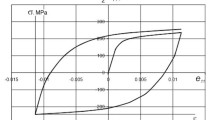
It is shown that, in the case of an axisymmetric stress state, the solution of the statically definable boundary-value problem for an ideal rigid-plastic body using the Mises-Schleicher strength criterion is extended to the rigid-creep model with any specified creep-rupture strength and corresponds to the limit state of a real creeping body.
Similar content being viewed by others
References
A. F. Nikitenko, “Limit state of a creeping body,” in: Problems of Optimal Design of Structures, Proc 2nd All-Russian Seminar (Novosibirsk, April 7–9, 1998, Novosibirsk), Univ. of Architecture and Civil Engineering, Novosibirsk (1998), pp. 94–103.
A. F. Nikitenko, “Kinetic creep theory and creep-rupture strength analysis for structural elements. 2. Limit state of nonuniformly heated structural elements,” Probl. Prochn., No. 6, 5–14 (2005).
L. M. Kachanov, Creep Theory [in Russian], Fizmatgiz, Moscow (1960).
A. F. Nikitenko, A. M. Kovrizhnykh, and I. V. Kucherenko, “Unified (generalized) criterion of material strength. 1,” Izv. Vyssh. Uchebn. Zaved., Striotel’stvovo, Nos. 11/12, 4–11 (2006).
L. M. Kachanov, Foundations of the Theory of Plasticity, North-Holland, Amsterdam-London (1971).
Yu. N. Rabotnov, Mechanics of Deformable Bodies [in Russian], Nauka, Moscow (1988).
Author information
Authors and Affiliations
Corresponding author
Additional information
__________
Translated from Prikladnaya Mekhanika i Tekhnicheskaya Fizika, Vol. 51, No. 1, pp. 147–152, January–February, 2010.
Rights and permissions
About this article
Cite this article
Nikitenko, A.F., Reznikov, B.S. Limit state of structural elements during inelastic deformation. J Appl Mech Tech Phy 51, 125–129 (2010). https://doi.org/10.1007/s10808-010-0019-9
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10808-010-0019-9