Abstract
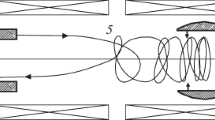
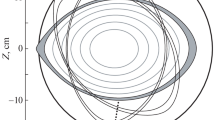
This paper considers various experimental designs on the Atlas facility to study the physics of liners and determine the optimum conditions of their stable motion. In one of the versions, in comparison with the Liner Demonstration series of experiments, in which unstable liner motion was observed, it is proposed to reduce the initial liner radius without changing its mass, which, according to two-dimensional calculations, should to lead to more stable motion of the liner with unchanged velocity. It is also proposed to perform an experiment in which periodic perturbations at a certain wavelength are created on the outer surface of the liner with a simultaneous increase in its thickness. According to calculations, the growth of chaotic perturbations is stabilized in this case with the preservation of the liner velocity.
Similar content being viewed by others
References
V. K. Chernyshev, V. N. Mokhov, M. S. Protasov, et al., “Liner ponderomotive units used as a driver in magnetic implosion systems,” Vopr. Atom. Nauki Tekh., Ser. Mat. Model. Fiz. Prots., No. 4, 42–50 (1992).
A. M. Buyko, V. V. Zmushko, P. N. Nizovtsev, et al., “On feasibility to achieve high longitudinal symmetry of cylindrical metal liners compressed by currents from most powerful disk EMG,” in: C. Stallings and H. Kirbie (eds.), Digest of Tech. Papers 12th IEEE Int. Pulsed Power Conf., Monterey (1999), pp. 1145–1148.
A. M. Buyko, O. M. Burenkov, V. V. Zmushko, et al., On the feasibility to achieve high pressures with disk EMG driven impacting liners,” in: R. Reinovsky and M. Newton (eds.), Digest of Tech. Papers: Pulsed Power Plasma Science-2001, Inst. of Electric. and Electron. Eng., Inc. (2001), pp. 516–519.
R. E. Reinovsky, W. E. Anderson, W. L. Atchison, et al., “Pulsed power hydrodynamics: A new application of high magnetic field,” in: V. D. Selemir and L. N. Plyashkevich (eds.), Proc. of the 9th Int. Conf. on Megagauss Magnetic Field Generation and Related Topics (Moscow-St. Petersburg, 2002), Inst. of Exp. Phys., Sarov (2004), pp. 696–705.
S. F. Garanin, V. I. Mamyshev, and V. B. Yakubov, “The MAGO system: current status,” IEEE Trans. Plasma Sci., 26, No. 4, 2273–2278 (2006).
J. H. Degnan, T. Cavazos, D. Clark, et al., “On research on magnetic pressure implosions of long cylindrical liners, suitable for subsequent compression of the field reversed configuration type of compact toroids,” in: V. D. Selemir and L. N. Plyashkevich (eds.), Proc. of the 9th Int. Conf. on Megagauss Magnetic Field Generation and Related Topics (Moscow-St. Petersburg, 2002), Inst. of Exp. Phys., Sarov (2004), pp. 730–737.
S. F. Garanin, G. G. Ivanova, D. V. Karmishin, and V. N. Sofronov, “Diffusion of a megagauss field into a metal,” J. Appl. Mech. Tech Phys., 46, No. 2, 153–159 (2005).
W. L. Atchison, R. J. Faehl, I. R. Lindemuth, et al., “Dependence of solid liner stability on drive conditions during magnetic implosion,” in: V. D. Selemir and L. N. Plyashkevich (eds.), Proc. of the 9th Int. Conf. on Megagauss Magnetic Field Generation and Related Topics (Moscow-St. Petersburg, 2002), Inst. of Exp. Phys., Sarov (2004), pp. 710–717.
A. M. Buyko, S. F. Garanin, D. V. Karmishin, et al., “Analysis of the liner stability in various experiments,” IEEE Trans. Plasma Sci., 36, No. 1, 4–9 (2008).
O. I. Volchenko, I. G. Zhidov, E. E. Meshkov, and V. G. Rogachev, “Development of localized perturbations on the unstable boundary of an accelerated liquid layer,” Pis’ma Zh. Tekh. Fiz., 15, No. 1, 47–51 (1989).
E. E. Meshkov, Rayleigh-Taylor Instability: Laboratory Experiments, Krasnyi Octyabr’, Saransk (2002).
R. Reinovsky, W. Atchison, and W. Anderson, et al., “Stability of magnetically imploded liners for high energy density experiments,” in: H. J. Schneider-Muntau (ed.), Proc. of the 8th Int. Conf. on Megagauss Magnetic Field Generation and Related Topics (Tallahassee, USA, 1998), World Sci., Singapore (2004), pp. 473–478.
S. F. Garanin, S. D. Kuznetsov, C. Ekdahl, et al., “On feasibility of Rayleigh-Taylor instability magnetic stabilization of liner implosions,” in: J. Schneider-Muntau (ed.), Proc. of the 8th Int. Conf. on Megagauss Magnetic Field Generation and Related Topics (Tallahassee, USA, 1998), World Sci., Singapore (2004), pp. 563–566.
E. G. Harris, “Rayleigh-Taylor instabilities of a collapsing cylindrical shell in a magnetic field,” Phys. Fluids, 5, No. 9, 1057–1062 (1962).
B. G. Anderson, W. E. Anderson, A. M. Buyko, et al., “Liner experiment on verification of Rayleigh-Taylor instability magnetic stabilization effect (joint LANL/VNIIEF experiment PEGASUS-2),” in: R. Reinovsky and M. Newton (eds.), Digest of Tech. Papers: Pulsed Power Plasma Science-2001, Inst. of Electric. and Electron. Eng., Inc. (2001), pp. 354–355.
A. M. Bujko, S. F. Garanin, V. A. Demidov, et al., “Investigation of the dynamics of a cylindrical exploding liner accelerated by a magnetic field in the megagauss range,” in: V. M. Titov and G. A. Shvetsov. Megagauss Fields and Pulsed Power Systems, Nova Sci. Publ., New York (1990), pp. 743–748.
I. D. Sofronov, S. A. Bel’kov, O. A. Vinokurov, et al., “Complex of MIMOZA-99 codes,” in: Trans. of the All-Russia Research Institute of Experimental Physics, All-Russia Research Institute of Experimental Physics, Sarov, (2001), pp. 94–101.
A. M. Buyko, S. F. Garanin, V. V. Zmushko, et al., “2D computations for perturbation growth of magnetically driven cylindrical aluminum and aluminum alloy liners,” in: E. Meshkov, Yu. Yanilkin, and V. Zhmailo (eds.), Proc. of the 7th Int. Workshop Phys. Compressible Turbulent Mixing (St. Petersburg, Russia, 1999), Inst. of Exp. Phys., Sarov (2001), pp. 237–243.
Ya. B. Zel’dovich and Yu. P. Raizer, Physics of Shock Waves and High-Temperature Hydrodynamic Phenomena, Academic Press, New York (1967).
P. R. Garabedian, “On steady-state bubbles generated by Taylor instability,” Proc. Roy. Soc. London, Ser. A, 241, p. 423 (1957).
Author information
Authors and Affiliations
Corresponding author
Additional information
__________
Translated from Prikladnaya Mekhanika i Tekhnicheskaya Fizika, Vol. 50, No. 3, pp. 3–14, May–June, 2009.
Rights and permissions
About this article
Cite this article
Buiko, A.M., Garanin, S.F., Zmushko, V.V. et al. On stabilization of implosion of condensed liners. J Appl Mech Tech Phy 50, 361–370 (2009). https://doi.org/10.1007/s10808-009-0049-3
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10808-009-0049-3