1 Introduction

Ion-exchange membranes have several industrial applications, including fuel cells, the Chlor–Alkali process, and water electrolysis. In order to explain the mass transfer in the membrane at high current densities, a suitable mathematical model is required. There are different approaches to describe the transport of ions inside the membrane. Rohman and Aziz have reviewed mathematical models of ion transport in electrodialysis. They have proposed three types of phenomenological equations in their irreversible thermodynamic approach: (1) the Maxwell–Stefan (MS) equation which takes the interaction between each pair of components into account; (2) the Kedem–Katchalsky (KK) equation that considers the membrane as a geometric transition region between two homogenous compartments; and (3) the Nernst–Planck (NP) equation which describes diffusion and electro-migration in the ionic transport without taking into account the interaction between ions. The latter is widely used because of its simplicity [1]. Psaltis et al. have compared the Nernst–Planck and Maxwell–Stefan approaches to transport predictions of ternary electrolytes. They have concluded that using binary diffusivities (neglecting interaction between different solute species) and the full Maxwell–Stefan model does not affect the final steady-state concentrations profiles in the electrolyte solution of a multicomponent system. This shows that using the effective diffusivities in the Nernst–Planck equation should give reasonable accuracy in the results [2]. Additionally, Graham et al. have shown that the Nernst–Planck equation is valid in modeling diffusion of ions in ion-exchange resins of high concentrations (3–4 M) if taking into account the effective diffusivities [3].

The morphological structure of an ion-exchange membrane is also important in modeling the transport process in the pore volume of the membrane. This is because any change in the morphology, i.e., the number and size of liquid pores, can alter the effective diffusivities inside the pores and as a result the transport process. There have been several studies on the morphological structure of ion-exchange membranes, particularly the Nafion membrane, i.e., core–shell model proposed by Fujimura et al. [4], a sandwich-like model proposed by Haubold et al. [5], and a rod-like model proposed by Rubatat et al. [5]. The cluster-network model presented by Mauritz et al. [6] is one of the earliest models widely used for understanding the properties of Nafion membranes. This model is based on small-angle X-ray scattering (SAXS) measurements and estimates the cluster network of Nafion to consist clusters with a diameter of ~4 nm with 1-nm channels connecting the pore clusters. Also, among the early models, Yeager et al. proposed a three-phase model without any strict geometry of the clusters with an interphase between the hydrophobic and hydrophilic regions [6]. Schmidt et al. simulated parallel water channel models for the structure of the Nafion membrane with water channel diameters of 1.8 and 3.5 nm with an average of 2.4 nm at 20 vol% water [7]. Gebel et al. have studied the structural evolution of perfluorosulfonated ionomer membranes from dry to a highly swollen state with small-angle X-ray scattering (SAXS) measurement [8]. They characterized the structural evolution of Nafion 115 and 117 of 1100 EW. They concluded that as the membrane gets hydrated and swells, the cluster sizes increase. As a result of opening up of the pores, the pore clusters connect. At even higher hydration level, the authors observed that the swelling process for water content larger than 50 % causes an inversion of the structure from a reverse micellar structure to a connected network of polymer rod-like particles [8]. Based on their assumption for water swollen state, the cluster radii is 2 nm and it increases to 2.09, 2.18, and 2.35 nm for the case of N-methylformamide, ethanol, and formamide, respectively [8].

The transport of ions in the membrane with the Nernst–Planck approach has been studied by other authors as well. Verbrugge et al. [9] have developed ion and solvent transport within a sulfuric acid/perfluorosulfonic acid membrane. Bouzek et al. [10, 11] also modeled the ion transport inside the membrane with and without considering the convection in the diffusion layer. They predict the ion transport in the membrane up to 2.5 kA m−2.

The purpose of this work is to develop a Nernst–Planck model that can describe the transport of ions in the membrane at high current densities. It is of great interest to understand the membrane performance in terms of voltage drop and permselectivity at high current densities, because the membrane has the biggest contribution to the cell voltage. Thus, it is vital to include the membrane performance in the assessment of the electrochemical cell performance and the process economics. In this study, the transport of species inside the pore volume of the membrane is described taking into account the effective diffusivities. Also, the morphological structure of the membrane in this study is based on the model from Schmidt et al. and Gebel because they give an indication of the size of channel diameters in dry and hydrated states. One difference to the approach in this study and the work of Verbrugge et al. [9] is that they use an empirical correlation for the partition coefficient at the solution–membrane interface. Here, a general Donnan equilibrium phenomenon is used to describe the boundary condition. In the work of Bouzek et al. [10, 11], the model is already assumed to be at steady-state and therefore requires accurate initial guesses to avoid convergence errors. In this study, the model is time-dependent and not sensitive to initialization. Also, Bouzek et al. use self-diffusion coefficients estimated by others, whereas here the free solution diffusivities are used to estimate diffusivities in the membrane. This is done by evaluating the channel size and porosity of the membrane. Additionally, the focus of this work is on the membrane performance at high current densities.

The Nernst–Planck model is fitted to experiments which are elaborated elsewhere [12]. The potential drop over the membrane and the membrane selectivity are determined from the ionic fluxes in the membrane for current densities up to 20 kA m−2 and in a 15 wt% sodium hydroxide solution.

2 Model approach

The Nernst–Planck equation for modeling the transport of ions in an ion-exchange membrane for an ideal solution can be written as Eq. (1) [13, 14]:

$$J_{i} = - D_{i} \nabla C_{i} - z_{i} D_{i} C_{i} \frac{F}{RT}\nabla \varphi + C_{i} v.$$
(1)

It consists of three transport terms: diffusion, electro-potential, and convection. The convection term is affected by the osmotic pressure and electro-osmotic effects, and it can be defined as Eq. (2) with the Schlögl equation [9, 15]. Electroneutrality is assumed everywhere in the membrane and at the interface of the membrane and solution (Eq. 3).

$$\nu = d_{h} (z_{m} C_{m} F\nabla \varphi - \nabla P),$$
(2)
$$\sum\limits_{i} {C_{i} z_{i} = } 0.$$
(3)

Schlögl has defined the hydrodynamic permeability of the membrane based on Hagen–Poiseuille presented in Eq. (4) [16]:

$$d_{h} = \frac{{d_{p}^{2} \varepsilon_{m} }}{32\eta }.$$
(4)

The Schlögl equation seems to be able to describe the convective velocity as a constant value in the membrane. Additionally, the mass continuity correlation (Eq. 6) is required to complete the system of transport equations. This means that the convective velocity needs to be defined at every position in the membrane. This is because the density changes with the variation of concentration inside the membrane. The convective velocity is calculated based in Eq. (2) at the left side of the membrane with an initial guess of the membrane voltage drop. Then, using the sodium hydroxide density correlation (Eq. 5) [17], the convective velocity is determined at every position inside the membrane. The relation between the current density and the flux of charged species is shown in Eq. (7). Equation (8) is derived by combining Eqs. (1) and (7) as an expression for the potential gradient. The voltage drop from Eq. (8) is then iterated using an initial guess until the solution is converged.

Equation (9) describes the water flux. The concentration of water inside the membrane is calculated based on the concentration of sodium and hydroxide ions at every position using the density correlation (Eq. (5)). It has been shown by several authors [12, 18–21] that water is not only transported in the hydrated shell of the positive ions, but also due to convection and the electromotive force.

$$\rho \times 10^{ - 3} = 1.006 + 0.0011W_{\text{NaOH}} - 0.172 \times 10^{ - 4} W_{\text{NaOH}}^{2} - 0.358 \times 10^{ - 3} T_{c} - 0.214 \times 10^{ - 5} T_{c}^{2} ,$$
(5)
$$- \nabla (\rho v) = 0,$$
(6)
$$I = F\sum\limits_{i = 1}^{n} {z_{i} J_{i} } ,$$
(7)
$$\nabla \varphi = \frac{{\frac{I}{F} + \sum\nolimits_{i = 1}^{n} {z_{i} D_{i} \nabla C_{i} - v\sum\nolimits_{i = 1}^{n} {z_{i} C_{i} } } }}{{ - \frac{F}{RT}\sum\nolimits_{i = 1}^{n} {z_{i}^{2} D_{i} C_{i} } }},$$
(8)
$$\rho v = \sum\limits_{\begin{subarray}{l} i = 1 \\ n \ne {\text{water}} \end{subarray} }^{n} {M_{i} N_{i} } + M_{\text{water}} N_{\text{water}} .$$
(9)

In literature, the electrical conductivity of a membrane has been defined based on Ohm’s law, \(I = \kappa \frac{{{\text{d}}\varphi }}{{{\text{d}}x}}\),using the Nernst–Planck flux equation, and also by neglecting the concentration gradient and convection [13, 14, 17]. This is debatable to be valid since our experimental results [12] show that the membrane conductivity depends not only on concentration and temperature but also on the current density. Additionally, we show here in Appendix A that the potential gradient is not constant, and its non-linear behavior is required to have equal fluxes at the left and right sides of the membrane at the steady-state condition. Equations (1) to (8) make the system of transport equations inside the membrane complete without taking into account the water dissociation effect. Water dissociation, proton, and hydroxyl ion production due to self-ionization of water is more important in anion-exchange membranes than in cation-exchange membranes [22–32]. Tanaka has studied the mechanism of concentration polarization and water dissociation in the boundary layer of ion-exchange membranes. He has shown that the water dissociation in the strong acid cation-exchange membrane is more suppressed than in the strong base anion-exchange membrane because the forward reaction rate constant in the cation-exchange membrane is lower. In fact, due to stronger repulsive forces between the fixed ionic groups of the cation-exchange membrane and the co-ions, the water dissociation reaction is suppressed [32]. Also, this study is at a high concentration of the electrolyte solution which is not known to cause water dissociation.

2.1 Boundary conditions [13, 33, 34]

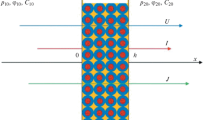
For the boundary condition, the flux of species at the steady-state should be equal at the membrane and solution interface which is shown in Eq. (10) for anode interface. This is similar for the cathode interface. The mass transfer at the membrane surface is assumed very high because of the very high mixing of the electrolyte at the membrane surface which is elaborated in our earlier paper [12]. Thus, the boundary layer thickness is calculated from the measured mass transfer in a rotor–stator spinning disc reactor which is proved to have a very high mass transfer coefficient [35]. The concentration jump of ionic species at the solution and the membrane interface for both anolyte and catholyte sides are depicted in Fig. 1.

Fig. 1
figure 1

Schematic drawing of the concentration of ionic species in the bulk solution, at the solution, and at the membrane interface for both anolyte and catholyte sides

Full size image
$$\frac{{D_{i}^{s} }}{{\delta_{\text{diff}} }}(C_{i}^{A,s} - C_{i}^{A,int} ) + vC_{i}^{A,int} \varepsilon = \left( { - D_{i} \frac{{{\text{d}}C_{i}^{{Am,\text{int} }} }}{{{\text{d}}x^{{\prime }} }} - z_{i} D_{i} C_{i}^{{Am,\text{int} }} \frac{F}{RT}\frac{{{\text{d}}\varphi }}{{{\text{d}}x^{{\prime }} }} + \nu C_{i}^{{Am,\text{int} }} \delta } \right)\frac{1}{\delta }\varepsilon .$$
(10)

The concentrations at the interface are defined based on the Donnan equilibrium phenomenon which is an electrochemical equilibrium between the membrane and solution phases (Eq. 11). At steady-state in equilibrium, the electrochemical potential of all ions in the membrane and the solution are equal [13]:

$$\mu_{i}^{m} + z_{i} F\varphi^{m} = \mu_{i}^{s} + z_{i} F\varphi^{s} .$$
(11)

The Donnan potential can be expressed with Eq. (12):

$$\varphi^{m} - \varphi^{s} = \frac{1}{{z_{i} F}}\left[RT\ln \frac{{a_{i}^{s} }}{{a_{i}^{m} }} + \overline{V}_{i} (P^{s} - P^{m} )\right] = \varphi_{\text{Don}} .$$
(12)

Here, the assumption of Higa et al. [34] that the surface of the membrane is always in the state of Donnan equilibrium with the same partition coefficient for all of the ions is used. This way the Donnan equilibrium gives a general correlation for all ions between the membrane and the external solution. This is shown in Eq. (13) in which the osmotic pressure is neglected:

$$\frac{{C_{i}^{m} }}{{C_{i}^{s} }} = {\text{e}}^{{\frac{{ - Fz_{i} \Delta \varphi_{\text{Don}} }}{RT}}} = K^{{z_{i} }} .$$
(13)

We have used the electroneutrality condition in the solution to derive a correlation (Eq. 14) that relates the solution interface concentration and the membrane interface concentration (See Appendix 3).

$$C_{{i,{\text{pos}}}}^{{A,\text{int} }} = C_{{i,{\text{pos}}}}^{m,0} \sqrt {\frac{{\sum\nolimits_{i}^{{N_{ions} }} {C_{{i,{\text{neg}}}}^{m,0} } }}{{\sum\nolimits_{i}^{{N_{ions} }} {C_{{i,{\text{pos}}}}^{m,0} } }}} ;\quad C_{{i,{\text{neg}}}}^{{A,\text{int} }} = C_{{i,{\text{neg}}}}^{m,0} \sqrt {\frac{{\sum\nolimits_{i}^{{N_{ions} }} {C_{{i,{\text{pos}}}}^{m,0} } }}{{\sum\nolimits_{i}^{{N_{ions} }} {C_{{i,{\text{neg}}}}^{m,0} } }}} .$$
(14)

It is also possible to define the membrane interface concentration based on the solution interface concentration using the electroneutrality condition in the membrane. However, it might require solving a quartic, quantic, etc. equations depending on the valence and the number of ions. This makes it more complicated to be solved.

2.2 Solver

The pdepe solver of MATLAB is used. It iterates the system of equations over time and uses one-dimensional space to obtain the solution at the steady state. The complete set of dimensionless equations is presented in detail in Appendix 2. The grid points are set in a logarithmic scale near the boundaries due to a larger gradient of concentration and linear in the center part.

2.3 Model assumptions

Constant pressure and temperature are assumed. The pressure contribution in the transport equations and Donnan equilibrium approach is neglected especially because the same concentration of sodium hydroxide as anolyte and catholyte is being used. Solutions are assumed to be ideal. Properties of the Nafion single-layer membrane, N-1110 [36], are used.

2.4 Constitutive equations

The initial water concentration inside the membrane is calculated based on the water uptake for perfluorinated membrane of 1100 EW as a function of sodium hydroxide concentration. The water uptake is presented in weight percentage of dry polymer in Eq. (15) [17].

$$W_{w} = - 0.0052 \times (0.001C_{\text{NaOH}} )^{3} + 0.165 \times (0.001C_{\text{NaOH}} )^{2} - 2.708 \times (0.001C_{\text{NaOH}} ) + 36.68.$$
(15)

In a polymeric matrix, the path length of diffusion is not a straight line. Thus, diffusion coefficients of ionic species in free water are used and converted into effective diffusivities. This is shown in Eq. (16) where the diffusivities in the polymer matrix and in the free water are related via tortuosity [37].

$$Dij = D^{s} ij/\tau .$$
(16)

The dependency of tortuosity to the polymer porosity has been shown in many models in the literature [38–41]. Here, the model predicted by Marshal which was used by Wesselingh is used to define the tortuosity as presented in Eq. (17) [37].

$$\tau = \varepsilon^{ - 1.5} .$$
(17)

Equation (18) defines the porosity of the membrane as the volume of pores with ion clusters divided by the total volume.

$$\varepsilon = \frac{{V_{\text{e}} f_{\text{e}} }}{{V_{\text{tot}} }} = \frac{{\frac{{W_{\text{e}} }}{{\rho_{\text{e}} }}}}{{\frac{1}{{\rho_{m} }} + \frac{{W_{\text{e}} }}{{\rho_{\text{e}} }}}}f_{\text{e}} .$$
(18)

W e and ρ e which are the weight fraction and the density of the adsorbed electrolyte are estimated based on the water uptake of the membrane (W o in Eq. 15) and the density of the water. f e is the fraction of electrolyte in the pores with ion cluster; it is estimated based on the work of Yeo et al. [42] to be 0.76. This gives an estimation of the membrane porosity as a constant parameter in the model. Also, the membrane is assumed to have stationary fixed charges and to consist of homogenous cylindrical channels. The concentration of the stationary fixed charges in the membrane is calculated from Eq. (19). It takes into account the density and weight fraction of the adsorbed electrolyte, equivalent weight (EW), which is defined as the weight of polymer in gram per mole of sulfonic acid groups, fraction of ionic groups, and electrolyte in the ion cluster [17, 42].

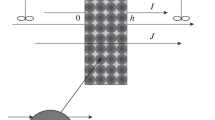
$$C_{m} = \frac{{1000 \times \rho_{\text{e}} }}{{EW \times W_{\text{e}} }}\left( {\frac{{f_{m} }}{{f_{\text{e}} }}} \right).$$
(19)

It has been discussed in literature that a Nafion membrane swells when hydrated [4–6, 8, 43]. After the model simulation with constant porosity and channel diameter, the ion transport through the membrane at high current densities is assumed to follow a similar trend as when the hydration level increases in the membrane. Apparently, increasing the current density results in opening up of the pore clusters and opening of the dead-end pores [6]. According to Takahashi et al. [44], the channel size should be dependent on the relationship between the inner stress due to the pressure inside the channel and the elasticity of the polymer matrix. Thus, due to higher mass flux under high current density, the inner stress increases and results in opening up of the pore channels [44]. The change in the pore size and opening of the dead-end pores are depicted in Fig. 2.

Fig. 2
figure 2

Simplified sketch of the membrane cross-sectional area consisting of homogenous cylindrical channels with open (active) pores and closed (inactive) pores of a a non-swollen membrane and b swollen membrane at high current densities

Full size image

Here, the assumption of the membrane swelling based on the work of Tiss et al. is used when performing the sensitivity analysis of the model. They assumed that the channels are oriented in the same direction in the membrane and are perpendicular to the membrane–liquid interface. The membrane porosity, which is the occupied volume fraction of the membrane by liquid, is assumed to have N number of cylindrical channels (N tot) per cross-sectional area. By taking into account the tortuosity effect, the total porosity can be calculated with Eq. (20):

$$\varepsilon^{\text{tot}} = N^{\text{tot}} \pi r_{p}^{2} \tau .$$
(20)

Combining Eqs. (17) and (20), the total and active porosities of the membrane are defined as a function of the total number of pores (N tot) and the pore radius (r p ) in Eqs. (21) and (22).

$$\varepsilon^{\text{tot}} = (N^{\text{tot}} \pi r_{p}^{2} )^{{\frac{2}{5}}} ,$$
(21)
$$\varepsilon^{\text{act}} = (N^{\text{act}} \pi r_{p}^{2} )^{{\frac{2}{5}}} .$$
(22)

The transport number presented in Eq. (23) is the fraction of current carried by a certain ion. It is an indication of the membrane permselectivity.

$$t_{i} = \frac{{J_{i} \times F}}{I}.$$
(23)

2.5 Model input parameters

Table 1 presents the input parameters used in the model based on the experimental condition and also the model assumptions. The outputs of the model are the concentration of ions in the membrane, fluxes, the membrane voltage drop, and the sodium transport number.

Table 1 Input parameters of the model
Full size table

3 Results and discussion

Figure 3 shows the profiles of concentration change for sodium, hydroxide, and water in the membrane over a dimensionless length of the membrane at the steady-state. The identical concentrations in the anolyte and catholyte bulk solution are shown as straight lines followed by the gradient in the boundary layer thickness. The concentration inside the membrane stands between the two vertical lines. Increasing the current density results in a lower concentration of ions in the membrane on the anode side and a higher concentration on the cathode side.

Fig. 3
figure 3

Concentration profiles of a sodium ions, b hydroxide ions, and c water inside the N-1110 membrane at the steady-state for current density range of 0–20 kA m−2 in 15 wt% sodium hydroxide solution as both anolyte and catholyte

Full size image

Figure 4 shows that the voltage drop and sodium transport numbers calculated for the model with constant porosity and active number of pores do not fit with the measured values in the experiment. The experiments were carried out on the mono layer Nafion N-1110 in an identical solution of 15 wt% sodium hydroxide at 40 °C [12]. The model shows a linear increase of the membrane voltage drop with current density and no dependence of sodium transport number on the current density. Since the model is unable to predict the membrane performance as a function of current density, the membrane swelling assumption as described in Sect. 2 is used to describe the membrane behavior at high current densities. As there are no measured data available for a change of membrane structure due to swelling, a range of pore diameters and number of active cylindrical pores are chosen based on the rough estimation of the found pore diameters in the literature [7, 8].

Fig. 4
figure 4

Membrane a voltage drop and b sodium transport number at the steady-state and current density range of 0.3–20 kA m−2 measured experimentally [12] and calculated for the base model

Full size image

Figures 5a, b presents the sensitivity analysis of the model over a range of membrane pore diameters, and active numbers of cylindrical pores at 10 and 20 kA m−2, respectively, for 2 × 1016 total number of the pores. The total number of pores is calculated from the properties presented in Table 1. It shows that for a certain total number of pores, there is a unique set of channel diameter and active number of pores that fit to the experimental values of the membrane voltage drop and sodium transport number.

Fig. 5
figure 5

Sensitivity analysis of membrane voltage drop and sodium transport number over a range of pore diameters (solid line d p, nm) and numbers of active pores (dashed line N act × 10−15) for a given 2 × 1016 total number of pores. The experimental membrane voltage drop and sodium transport number (dot) at a 10 kA m−2 and b 20 kA m−2 [12]

Full size image

The sensitivity analysis was performed at other current densities to fit the model to the experimentally measured values of the membrane voltage drop and sodium transport number. The fitted pore diameter and number of active pores used in the model that matched the experimental values of the voltage drop are presented in Fig. 6. The transport number is only fitted at the two available values of 10 and 20 kA m−2. Figure 6a shows how the pore diameter increases with increasing current density. Figure 6b shows the opening of the dead-end pores and activation of more cluster channels in transporting the ions though the membrane as a function of current density. This shows that increasing the current density results in swelling of the membrane due to an increase in channel diameter. Also, it predicts that with an increase in the current density, the number of active pores that participate in the ion transport increases, and possibly some of the dead-end pores open at high current densities. This way the model is able to give a better prediction of ion transport inside the membrane. At this stage, no better reasoning could be found to explain the observed trend of change in the membrane voltage drop and transport number with increasing current density. The proposed values of the channel diameter for a swollen membrane by others [7, 8] are an average of 20 nm for solutions other than sodium hydroxide which could be the reason of the different obtained optimized channel diameters here. It is worth mentioning that using the optimized channel diameters and the number of active pores at different current densities did not change the concentration profiles of the ions and water in the membrane.

Fig. 6
figure 6

The effect of current density on the membrane swelling and opening up of a the pore clusters and b the dead-end pores

Full size image

4 Conclusion

The transport of ions and water through a cation-exchange membrane has been mathematically modeled using the Nernst–Planck equation. For a single-layer Nafion N-1110 membrane, the model has been fitted to the measured values of the membrane voltage drop and sodium transport number at high current densities up to 20 kA m−2 using the membrane swelling assumption. Also, it is shown that the model is very sensitive to the pore diameter and the number of active pores. This could be because these parameters are a function of current density. Currently, we cannot find another reason to explain the observed behavior. With increasing current density, more charged ions rush into the membrane. Therefore, the membrane conductivity increases with current density. The change in pore diameter and number of active pores cannot be measured under transport conditions. The qualitative swelling model can explain the behavior of the membrane pore clusters at high current density.

We conclude that at high current densities the diameter of the pore channels is likely to increase due to the membrane swelling. This results in a higher number of active pores participating in transport of the ions through the membrane. It is believed that the membrane structure, i.e., channel size and porosity, has a high impact on the performance of this membrane in sodium hydroxide solution. Furthermore, it shows that there is a unique set of pore diameters and number of active pores that satisfy the experimental sodium transport number at a certain membrane voltage drop. This suggests that having a more in-depth knowledge of the membranes structure in a molecular level helps better understanding the ion transport in extreme operating conditions such as high current density.