1 Introduction

Current best-match retrieval models calculate some kind of score per collection item which serves as a measure of the degree of relevance to an input request. Scores are used in ranking retrieved items. Their range and distribution varies wildly across different models making them incomparable across different engines (Robertson 2007), even across different requests on the same engine if they are influenced by the length of requests. Even most probabilistic models do not calculate the probability of relevance of items directly, but some order-preserving (monotone or isotone) function of it (Nottelmann and Fuhr 2003).

For single-collection ad-hoc retrieval, the variety of score types is not an issue; scores do not have to be comparable across models and requests, since they are only used to rank items per request per system. However, in advanced applications, such as distributed retrieval, fusion, or applications requiring thresholding such as filtering, topic detection and tracking, or recall-oriented search, some form of score normalization or analysis is imperative. In the first two applications, several rankings (with non-overlapping and overlapping sets of items respectively) have to be merged or fused to a single ranking. Here, score normalization is an important step (Callan 2000). In practice, while many users never use meta-search engines directly, most conventional search engines have the problem of combining results from many discrete sub-engines. For example, blending images, text, inline answers, stock quotes, and so on, has become common.

In filtering and topic detection/tracking, bare scores give no indication on whether to retrieve an incoming document or not. Usually a user model is captured into some evaluation measure. Some of these measures can be optimized by thresholding the probability of relevance at some specific level (Lewis 1995), thus a method of normalizing scores into probabilities is needed. Additionally, thresholding has turned out to be important in recall-oriented retrieval setups, such as legal or patent search, where ranked retrieval has a particular disadvantage in comparison with traditional Boolean retrieval: there is no clear cut-off point where to stop consulting results (Oard et al. 2009). Again, normalizing scores to expected values of a given effectiveness measure allows for optimal rank thresholding. In any case, the optimal threshold depends on the effectiveness measure being used—there is no single threshold suitable for all purposes—and some of the measures require more complete distributional information on the relevant and non-relevant items than merely the probability of relevance.

Simple approaches, e.g. range normalization based on minimum and maximum scores, are rather naive, considering the wild variety of score outputs across search engines, because they do not take into account the shape of score distributions (SDs). Although these methods have worked reasonably well for merging or fusing results (Lee 1997), advanced approaches have been seen which try to improve normalization by investigating SDs. Such methods have been found to work at least as well as the simple ones (or in some cases better) in the context of fusion (Manmatha et al. 2001; Fernández et al. 2006a, b), and better in distributed retrieval (Arampatzis and Kamps 2009). They have also been found effective for thresholding in filtering (Arampatzis et al. 2000; Arampatzis and van Hameren 2001; Zhang and Callan 2001; Collins-Thompson et al. 2002) or thresholding ranked lists in recall-oriented setups (Arampatzis et al. 2009).

In this study, we review the history of modeling SDs in Information Retrieval (IR), focusing on the currently most popular model, namely, the mixture of normal-exponential, by investigating the theoretical as well as the empirical evidence supporting its use. We discuss conditions which any valid—from an IR perspective—binary mixture model should satisfy, such as the Recall-Fallout Convexity Hypothesis, and formulate new hypotheses considering the component distributions individually as well as in pairs. Although our contribution is primarily theoretical, we provide new experimental evidence concerning the range of retrieval models that the normal-exponential gives a good fit, and try to quantify the impact of non-convexity that the mixture possesses. Furthermore, we review recent non-binary approaches, speculate on graded relevance and on the use of logistic regression as a score calibration method. We formulate yet unanswered questions which should serve as directions for further research.

2 Modeling score distributions

Under the assumption of a binary relevance, classic attempts model SDs, on a per-request basis, as a mixture of two distributions: one for relevant and the other for non-relevant documents (Swets 1963; Swets 1969; Bookstein 1977; Baumgarten 1999; Arampatzis and van Hameren 2001; Manmatha et al. 2001). Given the two component distributions and their mix weight, the probability of relevance of a document given its score can be calculated straightforwardly (Arampatzis and van Hameren 2001; Manmatha et al. 2001), essentially allowing the normalization of scores into probabilities of relevance. Furthermore, the expected numbers of relevant and non-relevant documents above and below any rank or score can be estimated, allowing the calculation of precision, recall, or any other traditional measure at any given threshold enabling its optimization (Arampatzis et al. 2009). Assuming the right component choices, such methods are theoretically ‘clean’ and non-parametric.

Various combinations of distributions have been proposed since the early years of IR—two normal of equal variance (Swets 1963), two normal of unequal variance or two exponential (Swets 1969), two Poisson (Bookstein 1977), two gamma (Baumgarten 1999)—with currently the most popular model being that of using a normal for relevant and an exponential for non-relevant, introduced by Arampatzis et al. (2000); Arampatzis and van Hameren 2001 and followed up by Manmatha et al. (2001), Zhang and Callan (2001), Collins-Thompson et al. (2002) and others. For a recent extended review and theoretical analysis of those early proposals, we refer the reader to Robertson (2007). The latest improvements of the normal-exponential model use truncated versions of the component densities, trying to deal with some of its shortcomings (Arampatzis et al. 2009). In Sect. 3 we will focus on the original normal-exponential model. Then, in Sects. 4 and 5 we will see conditions that SD models should satisfy under some hypotheses. In Sect. 6, we will analyze the most recently proposed mixture model which uses a gamma for non-relevant and a mixture of n normals for relevant (Kanoulas et al. 2009). In Sect. 7, we will note practical problems and limitations of mixture models irrespective of the component choices.

Modeling SDs without reference to relevance seems to overcome some of the practical problems of mixture models. A recent attempt models aggregate SDs of many requests, on per-engine basis, with single distributions (Fernández et al. 2006a, b); this enables normalization of scores to probabilities—albeit not of relevance—comparable across different engines. The approach was found to perform better than the simple methods in the context of fusion (Fernández et al. 2006a, b). Nevertheless, it is not clear—if it is even possible—how using a single distribution can be applied to thresholding, where for optimizing most common measures a reference to relevance is needed. We will investigate such methods in Sect. 8.

One possible approach to modeling SDs is to first transform the scores into some form which exhibits better distributional properties. In principle any monotonic transformation of the scores produced by a system (which necessarily leaves the ranking unchanged) would be a candidate for this process. Thus one might for example transform a score which appeared to give a lognormal distribution for some relevance class, into one which gave a normal distribution, by taking the log of the score. This line has not in general been followed in the literature, and is not pursued here. However, we could go further, and attempt to transform the score into a probability of relevance. For at least some purposes for which knowledge of SDs would otherwise be useful, a calibrated probability of relevance would serve equally well. For example if the task is optimising a threshold for certain effectiveness measures, a probability of relevance of each ranked document would provide a suitable mechanism. One approach along these lines is provided by logistic regression, discussed further in Sect. 9.

3 The normal-exponential model

In this section, we review the normal-exponential model. We investigate the theoretical as well as the empirical evidence and whether these support its use.

3.1 Normal for relevant

A theorem by Arampatzis and van Hameren 2001 claims that the distribution of relevant document scores converges to a Gaussian central limit (GCL) quickly, with ‘corrections’ diminishing as O(1/k) where k is the query length. Roughly, three explicit assumptions were made:

  1. 1.

    Terms occur independently.

  2. 2.

    Scores are calculated via some linear combination of document term weights.

  3. 3.

    Relevant documents cluster around some point in the document space, with some hyper-ellipsoidal density (e.g. a hyper-Gaussian) with tails falling fast enough.

Next, we re-examine the validity and applicability of these assumptions in order to determine the range of retrieval models for which the theorem applies.

Assumption 1 is generally untrue, but see the further discussion below. Assumption 2 may hold for many retrieval models; e.g. it holds for dot-products in vector space models, or sums of partially contributing log-probabilities (log-odds) in probabilistic models. Assumption 3 is rather geometric and better fit to vector space models; whether it holds or not, or it applies to other retrieval models, is difficult to say. Intuitively, it means that the indexing/weighting scheme does its job: it brings similar documents close together in the document space. This assumption is reasonable and similar to the Cluster Hypothesis of van Rijsbergen (1979, Chap. 3).

Putting it all together, the proof is more likely to hold for setups combining the following three characteristics:

  • Vector space model, or some other geometric representation.

  • Scoring function in the form of linear combination of document term weights, such as the dot-product or cosine similarity of geometric models or the sum of partially contributing log-probabilities of probabilistic models.

  • Long queries, due to the convergence to a GCL depending on query length.

This does not mean that there exists no other theoretical proof applicable to more retrieval setups, but we have not found any in the literature.

A note on term independence.

Term independence assumptions are common in the context of probabilistic models and elsewhere, but are clearly not generally valid. This has elicited much discussion. The following points have some bearing on the present argument:

  • Ranking algorithms derived from independence models have proved remarkably robust, and unresponsive to attempts to improve them by including dependencies.

  • Making the independence assumption conditional on relevance actually makes it a little more plausible than a blanket independence assumption for the whole collection.

  • Cooper (1991) has shown that for the simple probabilistic models, one can replace the independence assumptions with linked dependence (that is, linked between the relevant and non-relevant sets), and end up with the same ranking algorithms. This may be a partial explanation for the robustness of the independence models.

  • This linked dependence assumption unfortunately does not help us with the present problem.

  • Cooper et al. (1992) show that if we want to estimate an explicit, well-calibrated probability of relevance for each document (to show to the user), then corrections need to be made to allow for the inaccuracies of the (in)dependence assumptions.

What these points emphasise is the very strong distinction between on the one hand having a scoring system which ranks well and on the other hand placing any stronger interpretation on the scores themselves.

3.2 Exponential for non-relevant

Under a similar set of assumptions and approximations, Arampatzis and van Hameren (2001) investigate also the distribution of non-relevant document scores and conclude that a GCL is unlikely and if it appears it does only at a very slow rate with k (practically never seen even for massive query expansion). Although such a theorem does not help much in determining a usable distribution, under its assumptions it contradicts Swets’ use of a normal distribution for non-relevant (Swets 1963, 1969).

The distribution in question does not necessarily have to be a known one. Arampatzis and van Hameren (2001) provide a model for calculating numerically the SD of any class of documents (thus also non-relevant) using Monte-Carlo simulation. In absence of a related theory or a simpler method, the use of the exponential distribution has been so far justified empirically: it generally fits well to the high-end of non-relevant item scores, but not to all.

3.3 Normal-exponential in practice

The normal-exponential mixture model presents some practical difficulties in its application. Although the GCL is approached theoretically quickly as query length increases, practically, queries of length above a dozen terms are only possible through relevance feedback and other learning methods. For short queries, the Gaussian may simply not be there to be estimated. Empirically, using a vector space model with scores which were unbounded above on TREC data, Arampatzis and van Hameren (2001) found usable Gaussian shapes to form at around k = 250. k also seemed to depend on the quality of a query; the better the query, the fewer the terms necessary for a normal approximation of the observed distribution. Along similar lines, Manmatha et al. (2001) noticed that better systems (in terms of average precision) produce better Gaussian shapes.

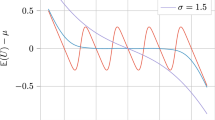
It was also shown in previous research that the right tail of the distribution of non-relevant document scores can be very well approximated with an exponential: Arampatzis and van Hameren (2001), Collins-Thompson et al. (2002) fit on the top 50–100, Manmatha et al. (2001) fit on almost the top-1,000 (1,000 minus the number of relevant documents). Arampatzis (2001) even fits on a non-uniform sample of the whole score range, but the approach seems system/task-specific. In general, it is difficult to fit an exponential on the whole score range. Figure 1 shows the total score densities produced by a combination of two queries and two sub-collections using kl-divergence as a retrieval model. Obviously, none of these SDs can be fitted in totality with the mixture. Candidate ranges are, in general, [s peak,  +∞) where s peak is set at the most frequent score or above.

Fig. 1
figure 1

KL-divergence score densities; two queries on two collections

Full size image

Despite the above-mentioned practical problems, Manmatha et al. (2001) used the model with success, with much shorter queries and even with a scoring system which produces scores between 0 and 1 without worrying about the implied truncation at both ends for the normal and at the right end for the exponential. In the context of thresholding for document filtering, with the generally unbounded scoring function BM25 and a maximum of 60 query terms per profile, the method performed well (2nd best, after Maximum Likelihood Estimation) on 3 out of 4 TREC data sets (Collins-Thompson et al. 2002).

3.4 Normal-exponential fits of TREC 2004 Robust track runs

To further determine the retrieval models whose observed SDs can be captured well with a normal-exponential mixture, we investigated all 110 submissions to the TREC 2004 Robust track. This track used 250 topics combining the ad-hoc track topics in TRECs 6–8, with the robust track topics in TRECs 2003–2004. Table 1 shows the 20 submissions where the mixture obtained the best fit as measured by the median upper-probability using the χ2 goodness-of-fit test. The table shows the run names; the used topic fields; the median χ2 upper probability indicating the goodness-of-fit; and the correlation between the optimal F 1@K (with K a rank) based on the qrels and on the fitted distributions. The two remaining columns will be discussed in Sect. 4. Not surprisingly, over all runs, the 20 runs with the best fit also tend to have better predictions of F 1@K. Footnote 1

Table 1 Twenty submissions with the best normal-exponential goodness-of-fit
Full size table

Looking at the retrieval models resulting in the best fits, we see seven runs of Peking University (icl) using a vector space model and the cosine measure. We also see 6 runs of Sabir Research, Inc. (SABIR) using the SMART vector space model. There are 3 runs of the University of Glasgow (uog) using various sums of document term weights in the DRF-framework. Two runs from Indiana University (wdo) using Okapi BM25. Finally, a single run from the Chinese Academy of Science (NLPR) using Okapi BM25, and one from Fundazione Ugo Bordoni (fub) also using sums of document term weights in the DRF-framework. Overall, we see support for vector space or geometrical models as being amenable to the normal-exponential mixture, as well as BM25.

Looking at query length, we see only 3 systems using the short title statement, and 8 systems using all topic fields. Many of the systems used query expansion, either using the TREC corpus or using the Web, leading to even longer queries. While longer queries tend to lead to smoother SDs and improved fits, the resulting F 1@K prediction seems better for the short title queries with high quality keywords. The ‘pos2’ runs of Peking University (icl) only index verbs and nouns, and considering only the most informative words seems to help distinguish the two components in the mixture.

4 The Recall-Fallout Convexity Hypothesis

From the point of view of how scores or rankings of IR systems should be, Robertson (2007) formulates the Recall-Fallout Convexity Hypothesis:

  • For all good systems, the recall-fallout curve (as seen from the ideal point of recall = 1, fallout = 0) is convex.

Similar hypotheses can be formulated as conditions on other measures, e.g., the probability of relevance should be monotonically increasing with the score; the same should hold for smoothed precision. Although, in reality, these conditions may not always be satisfied, they are expected to hold for good systems, i.e. those producing rankings satisfying the probability ranking principle (PRP), because their failure implies that systems can be easily improved as we explain next.

As an example, let us consider smoothed precision. If it declines as score increases for a part of the score range, that part of the ranking can be improved by a simple random re-ordering (Robertson 1969). This is equivalent of ‘forcing’ the two underlying distributions to be uniform in that score range. This will replace the offending part of the precision curve with a flat one—the least that can be done—improving the overall effectiveness of the system. In fact, rankings can be further improved by reversing the offending sub-rankings; this will force the precision to increase with an increasing score, leading to better effectiveness than randomly re-ordering the sub-ranking.

Such hypotheses put restrictions on the relative forms of the two underlying distributions. Robertson (2007) investigates whether the following mixtures satisfy the convexity hypothesis: two normals, two exponentials, two Poisson, two gamma, and normal-exponenttial. From this list, the following satisfy the hypothesis: two normal (only when their variances are equal), two exponential, two Poisson, and two gamma (for a quite wide range of parameters but not all).

Let us consider the normal-exponential mixture which violates such conditions only (and always) at both ends of the score range. Although the low-end scores are of insignificant importance, the top of the ranking is very significant. The problem is a manifestation of the fact that a normal falls more rapidly than an exponential and hence the two density functions intersect twice. Figure 2 depicts a normal-exponential fit on score data, together with the estimated precision and recall. The problem can be seen here as a declining precision above score 0.25.

Fig. 2
figure 2

Non-convexity inside the observed score range of a normal-exponential fit

Full size image

Let us now see how the problem is dealt with in practice. In adaptive filtering, Arampatzis et al. (2000), Arampatzis (2001) deal with the problem by selecting as filtering threshold the lower solution of the 2nd degree equation resulting from optimizing linear utility measures, while Zhang and Callan (2001), Collins-Thompson et al. (2002) do not seem to notice or deal with it. In meta-search, Manmatha et al. (2001) noted the problem and forced the probability to be monotonic by drawing a straight line from the point where the probability is maximum to the point [1,1]. Both procedures, although they may have been suitable for the above tasks, are theoretically unjustified. In Arampatzis et al. (2009), the two component distributions were set to uniform within the offending score range; as noted above, this is equivalent to randomization.

The problem does not seem severe for thresholding tasks. For example, Arampatzis et al. (2009) tried to optimize the F 1 measure and found that the impact of randomization on thresholding is that the SD method turns ‘blind’ inside the offending range. As one goes down the corresponding ranks, estimated precision would be flat, recall naturally rising, so the optimal F 1 threshold can only be below the range. On average, the optimal rank threshold is expected to be deeper than the affected ranks, so the impact of non-convexity on thresholding deemed to be insignificant. Sometimes the problem may even appear above the maximum observed score. Furthermore, the truncated normal-exponential model used in Arampatzis et al. (2009) also helped to alleviate non-convexity by sometimes out-truncating it; a modest and conservative theoretical improvement over the original model which always violates the hypothesis.

4.1 Non-convexity of TREC 2004 Robust track runs

To further determine the effect of the non-convexity of the normal-exponential, we again investigate the 110 submissions to the TREC 2004 Robust track. Table 1 also shows the median rank at which the estimated precision peaks (hence there is a non-convexity problem before this rank). We also show the effect of inverting the initial non-convex ranks, in percentage of overall MAP. That is, if precision increases up to rank 3 then it should make sense to invert the ranking of the first 2 documents. Two main observations are made. First, the median rank down to which the problem exists is very low, in the range of 1 (i.e. no practical problem) to 4, suggesting a limited impact on at least half the topics. Although there are outlier topics where the problem occurs far down the ranking, some of these may be due to problematic fits (Arampatzis et al. 2009). Second, ‘fixing’ the problematic initial ranks by inverting the order leads to a loss of MAP throughout. This signals that the problem is not inherent in the underlying retrieval model violating the PRP. Rather, the problem is introduced by the fitted normal-exponential; both practical and fundamental problems can cause a misfit given the limited information available.

In the bottom line, the PRP dictates that any theoretically sound choice of component densities should satisfy the convexity condition; from all the mixtures suggested in the past, the normal-exponential as well as the normal-normal of unequal variances do not, for all parameter settings. In practice, the problem does not seem to be severe in the case of normal-exponential; the affected ranks are usually few. Given the theoretical and empirical evidence, we argue that the problem is introduced by the exponential, not by the normal. Moreover, many distributions—especially ‘peaky’ ones—have a GCL. For example, assuming Poisson-distributed relevant document scores, for a system or query with a large mean score the Poisson would converge to a normal.

5 In-the-limit hypotheses

The Recall-Fallout Convexity Hypothesis considers the validity of pairs of distributions under the PRP. There are some reasons for considering distributions in pairs, as follows:

  • The PRP is about the relative ranking of relevant and non-relevant documents under conditions of uncertainty about the classification; it makes no statements about either class in isolation.

  • Consideration of the pair makes it possible for the hypothesis to ignore absolute scores, and therefore to be expressed in a form which is not affected by any monotonic transformation of the scores. Since ranking itself is not affected by such a transformation, this might be considered a desirable property.

  • If we wish in the future to extend the analysis to multiple grades of relevance, a desirable general form would be a parametrised family of distributions, with different parameter values for each grade of relevance (including non-relevance), rather than a separately defined distribution for each grade.

However, the evidence of previous work suggests that the distributions of relevant and non-relevant look very different. This renders the third point above difficult to achieve, and further suggests that we might want to identify suitable hypotheses to apply to each distribution separately. Here we consider two hypotheses, the first of which achieves some degree of separation but may be difficult to support; the second is expressed in relative terms but may be more defensible.

Note that both hypothesis are ‘in the limit’ conditions—they address what happens to the SDs under some limiting conditions of parameter values. They do not address the behaviour of distributions in other than these limiting conditions. Therefore they do not imply anything like the Recall-Fallout Convexity Hypothesis under actually observed parameter values.

5.1 The strong hypothesis

The ultimate goal of a retrieval system is not to produce some SD, but rather deliver the right items. In this light, the observed SD can be seen as an artifact of the inability of current systems to do a direct classification. Therefore, the ultimate SD all systems are trying to achieve is to the one with all relevant documents at the same high score s max, and all non-relevant documents at the same low score s min. The better the system, the better it should approximate the ultimate SD. This imposes restrictions on the two underlying components:

The strong SD hypothesis

For good systems, the score densities of relevant and non-relevant documents should be capable of approaching Dirac’s delta function, shifted to lie on the maximum score for the relevant and on the minimum score for the non-relevant, in some limiting condition.

Let us now investigate which of the historically suggested distributions can approximate a delta and how.

The normal goes to delta via σ → 0, and it can be positioned on demand via μ. The exponential approximates delta only via λ → +∞. The Poisson has one parameter λ, which incidentally equals both its mean and variance. For large λ, it approximates a normal with a mean and variance of λ. Consequently, as λ grows, the variance grows as well and it will never reach a delta. At the other side, for λ = 0 it becomes Kronecker’s delta, i.e. the discrete analogue of Dirac’s delta. The gamma has two parameters, \(\Upgamma(k,\theta)\). For large k it converges to a Gaussian with mean kθ and variance kθ2. The variance grows with k, but for θ → 0 it declines faster than the mean. So, the gamma can approximate a delta via an increasingly narrow Gaussian, and it can be positioned on demand via proper choices of k and θ.

Consequently, under the Strong SD Hypothesis, good candidates for relevant document scores are the normal or gamma, while for non-relevant are the normal, Poisson, exponential, or gamma. We only manage to reject the use of exponential and Poisson for relevant; although these could be simply shifted at s max or vertically mirrored to end at s max, those setups would seem rather strange and unlikely.

Considering the historically suggested pairs of distributions, we can reject the mixture of two exponentials—at least as it was suggested by Swets (1969): while the non-relevant exponential can approximate δ(s − s min) for λ → +∞, the relevant exponential cannot approximate δ(s − s max) for any λ. The two Poisson mixture of Bookstein (1977) is similarly rejected. The pairs remaining are the two normal, two gamma, or normal-exponential. Since a normal for non-relevant is unlikely according to Arampatzis and van Hameren (2001) and Sect. 2, that leaves us with the two gamma or normal-exponential with only the former satisfying the convexity hypothesis for a range of parameter settings—not all. Note also that the two exponential or two Poisson constructions with the relevant component vertically mirrored would violate the Recall-Falout Convexity Hypothesis.

5.2 The weak hypothesis

The strong SD hypothesis would like to see all relevant documents at the same (high) score, and all non-relevant documents at the same (low) score. This requirement is not really compatible with any notion that there may actually be degrees of relevance (even if the user makes a binary decision), and is also not necessary for perfect ranking performance—either or both classes might cover a range of scores, provided only that they do not overlap. Thus we can formulate a weaker hypothesis:

The weak SD hypothesis

For good systems, the score densities of relevant and non-relevant documents should be capable of approaching full separation in some limiting condition.

Clearly, the strong hypothesis implies the weak hypothesis, because the Dirac delta function gives full separation.

The weak hypothesis, however, would not reject the mixture of two exponentials: as we push the mean of the non-relevant distribution down, non-relevant scores are increasingly concentrated around zero, while if we push the mean of the relevant distribution up, the relevant scores are more and more widely spread among high values. In the limit, perfect separation is achieved. The weak hypothesis also does not reject the Poisson mixture, if we achieve the limit by letting lambda go to zero for non-relevant and to infinity for relevant. This is similar to the mixture of two exponentials, except that the relevant scores are uniformly distributed over the positive integers only, instead of the positive real line.

The weak hypothesis is indeed weak, in that it does not reject any of the combinations previously discussed. However, it reveals significant differences in the notions of ‘perfect’ retrieval effectiveness implicit in different combinations (and therefore what form improvements should take in SD terms). This ‘in the limit’ behaviour is worth further exploration.

6 Beyond-binary mixtures and grades of relevance

We may model SDs by means of more than two component distributions. In Kanoulas et al. (2009), for example, non-relevant item scores are modeled with a gamma and relevant scores with a mixture of n normals. The argument for doing so has been mostly empirical, but the authors provide some intuition behind the choice the distributions based on the number of matching terms between query and items. Roughly, different amounts of matching terms in relevant items would produce different normals. A weaker argument, in our opinion, is given for modeling the non-relevant with a gamma. That is, the contribution of two or more matching terms to the final score is often very different, and averaging such effects would be likely to produce a ‘hill’ of score frequencies (rather than a monotonically decreasing density).

Next, we investigate the n-normals-gamma model and provide stronger theoretical arguments for its use over the normal-exponential. Moreover, we present theoretical and empirical evidence [via post-analysis of the experimental results of Kanoulas et al. (2009)] that shows that the n-normals-gamma is a generalization of the normal-exponential and both models may converge to similar fits with increasing query length, as long as the exponential is fitted only to the high-end of non-relevant scores.

6.1 n-Normals-gamma versus normal-exponential

There are fundamental differences between the early proponents of the normal-exponential model. Arampatzis and van Hameren (2001) claimed a normal for relevant only via a Gaussian central limit (GCL) tied to query length and only for scoring functions of the form of linear combinations of query term weights. They also claimed just an approximation with an exponential of the high-end of non-relevant scores. Manmatha et al. (2001), and most studies afterwards, have ignored the effect of query length or scoring function on the shape of the relevant SD, and also some have used an exponential to model the non-relevant in the whole score range. While these simplifications may have haunted previous empirical results, the n-normals-gamma model does not suffer from them since it is a generalization with a better agreement to what was originally proposed by Arampatzis and van Hameren (2001).

First of all, Kanoulas et al. (2009) implicitly assume linear scoring functions. Let us now consider each item category individually. The shape of the SD of relevant items can be arbitrary before a GCL is reached. A strong argument for using a n-Gaussian mixture is that it is the simplest method that—for a sufficiently large n—can model arbitrary distributions, as well as a GCL for n = 1. Footnote 2 To strengthen also the ‘hill’ argument of Kanoulas et al. (2009) for the non-relevant SD, consider an extreme query consisting of all terms of an indexed collection. Against such a query, all non-relevant items will get non-zero scores, shifting the mode of the corresponding SD above zero. A gamma provides more flexibility to capture such effects, while it can still degenerate into an exponential (for a shape parameter k = 1) when queries are short. In any case, a gamma tail can be approximated by an exponential.

Kanoulas et al. (2009) show that the relevant SD of 70% of the topics can be fitted better with 2 Gaussians and only 30% are fitted better with a single one. Footnote 3 They also provide the distribution of the shape parameter k of the fitted gammas, which has a mean of 1.3 and a mode of around the same value. In a post-analysis of their experimental evidence it seems that as query length increases—from using only the topic title to using the title, description, and narrative—the number of topics better fitted with a single Gaussian increases at the expense of 2-Gaussian fits. Moreover, the mode of the distribution of k seems to slightly increase away from 1 with increasing query length. These observations support our arguments on the existence of a relevant GCL and generally a non-exponential non-relevant SD.

To evaluate the quality of the total fits, Kanoulas et al. (2009) report the root mean square (RMS) error as well as the mean absolute error (MAE) between the actual and the predicted precision at all recall levels for n-normals-gamma and normal-exponential for four retrieval models. Overall, the n-normals-gamma outperforms the normal-exponential at all query lengths. However, our post-analysis shows that, as query length increases, the percentage difference between the errors of two models slightly narrows: from 19–29% (depending on the retrieval model) to 18–23% in RMS error, and from 24–37% to 27–33% in MAE. This apparent convergence of the two models can only come from the relevant component since—as we argued and showed above—increasing query length worsens the exponential fits on the total non-relevant SDs; however, this could have been neutralized by fitting only the high-end of non-relevant scores.

6.2 Grades of relevance

Although this is not one of the motivations proposed in Kanoulas et al. (2009), one possible interpretation of the n-normals-gamma model is that it represents grades of relevance. That is, we might hypothesise that there are multiple grades of relevance (other than non-relevant) and that each grade has its own normal distribution of scores. The usual hypothesis of binary relevance is certainly an over-simplification, and it is worth considering what a generalised model, not making this assumption, should look like. Here we first give an idealised version of a very general model, and then return to a discussion of the n-normals-gamma model.

A general model of relevance, which would fit reasonably with a variety of experimental evidence over a long period, might be as follows. We assume that there is some underlying continuous relevance variable ranging from not-at-all to very highly relevant (in other words it would include non-relevance). Such a model was proposed in Robertson (1977); the continuous variable is there named synthema, which name we also use here for convenience. We then assume that assigning binary or graded relevance involves the setting of thresholds on synthema. Thus in obtaining relevance judgements, in any specific set of categories (binary or multiple), we observe only a bucketted version of synthema. The true continuous synthema remains hidden. We also have to consider that the observations may be noisy; noise may be present in both in the user’s assessment of the position of the individual document on the synthema scale, and in the user’s location of the thresholds on the scale.

Now, if we wish to combine this model with the notion of score distributions, the most natural model would be as follows. The score distribution should belong to a single family parameterised by the same synthema variable. In other words a given document with given synthema would be assumed to have a score drawn from the corresponding member of the distribution family. We would naturally assume (for a reasonable system) that the mean of the distribution would be a monotonic function of synthema. To put it another way, the score would be assumed itself to be a noisy estimate of synthema (up to a monotonic transformation).

Superficially, this model suggests that in the binary case we should be looking for models where both the relevant and non-relevant distributions come from the same family—e.g. normal-normal rather than normal-exponential or normal-gamma. However, the situation is somewhat more complex, because of the bucketting. Bucketting suggests that each of the two observed distributions is a mixture of a large number of distributions from the family, rather than a single one (noisy bucketting just reinforces this suggestion). We might now take this as an explanation for why the non-relevant distribution looks somewhat different from the relevant. What we actually observe is a mixture of a very large number of distributions (over a large range of the synthema scale), with (probably) a very heavy bias towards the very low end of the scale. Thus even if the original distribution family was the normal, we could easily get from this mixture process something like the very skewed distributions of non-relevant scores that we do in fact observe.

Turning to the relevants, the spread of synthema values is likely to be much less skewed, but also the actual examples are very sparse. It is clear that a small number of documents cannot support estimation of a large number of distributions, so that the technique adopted in Kanoulas et al. (2009) only indicates a minimum number of normals to make sense of the data.

It would be possible to devise some tests of these ideas using test data with multigraded relevance judgements. We leave such experiments for later work. We also note that we need to investigate the generalisation of the convexity or other hypotheses to this situation.

6.3 Summary

The n-normals-gamma model is a generalization of the normal-exponential which, due to its increased degrees of freedom, provides better fits than the latter when queries are not long enough for a relevant component GCL and at the same time are not too short to result in an exponential non-relevant component. Additionally, the n-normals can approximate arbitrary densities for a sufficiently large n, fitting retrieval models with relevant SDs not adhering to normal. Nevertheless, considering that a gamma tail can be approximated by an exponential and assuming long enough queries producing a GCL, one may instead find practically easier and sufficient to fit a normal-exponential on the high-end of scores due to fewer parameters involved.

It is easy to see that the n-normals-gamma model violates the Convexity Hypothesis for some parameter values, e.g. at least for the ones that it degenerates to a normal-exponential but even for more than those. It cannot be rejected, however, by either the Strong or the weak hypothesis, and it may be suitable for dealing with more than two grades of relevance.

7 Practical problems of mixture models

All mixture models irrespective of their component choices present some practical problems. Estimating the component densities is best done when many relevance judgements are available. In practice, relevance judgements are not available at all, or they are sparse, incomplete, or biased, making the estimation of the components of a mixture difficult. Much recent work on evaluation has focussed on the issues of evaluating (e.g. estimating evaluation metrics) with limited judgements, or of choosing which documents to have judged to optimise the estimation. We note that there has been no comparable work on estimating the shapes and/or parameters of score distributions from limited judgements.

In the contexts of meta-search (Manmatha et al. 2001) and in adaptive filtering (Arampatzis 2001), the authors tried to recover the mixing parameter and the parameters of the component normal and exponential densities without using any relevance judgements. The standard iterative approach expectation maximization (EM) (Ripley and Hjort 1995) was used with some success. The method can be modified to take into account relevance judgements, if any, nevertheless, it was found to be ‘messy’ and difficult to tune. It was very sensitive to the choice of the initial parameter values in converging to a global optimum rather than a local one.

As noted recently in Arampatzis and Kamps (2008), EM has also the of ‘problem’ of treating all data equally, while we are more interested in the top of the ranking/scores in IR. The problem manifests as a ranking-length bias: the more the score data, the lower the estimated threshold. In similar lines, regression (which we will see in Sect. 9) has the same problem: it optimizes the overall performance but not necessarily the retrieval quality at the top of the ranking, as noted in Fuhr et al. (1993). For that reason, Cooper et al. (1994) used only the top-ranked data for training.

When normalizing scores (especially of non-cooperative search engines), one should keep in mind that systems produce scores in order to rank documents, and do not care about the scale or shape of the scoring function. Therefore, system components which do not affect rankings may be added or removed arbitrarily, in order to, e.g., simplify calculations. Components which affect only the scale are not a problem for mixture models. However, many transformations affect the shape as well, e.g. using a logistic function to map (−∞, +∞) to [0,1]; in such cases, the initial choice of the density components may not apply any longer.

8 Single distribution approaches

The analysis of previous sections suggests that the normal-exponential mixture is not universal in modeling SDs in IR; some retrieval models perhaps could better be fitted with different mixtures, as in the case of kl-divergence (Fig. 1). Furthermore, the model has a serious theoretical problem: it does not satisfy the convexity condition, i.e. the output score does not monotonically increase with the input score. The problem shows always at the top of rankings, and it does not seem to be severe for thresholding tasks where an optimal threshold may often be lower than the non-convex ‘blind’ range, depending on the measure under optimization (Arampatzis et al. 2009). The problem is more acute in environments favoring initial precision such as in meta-search and distributed retrieval.

To make things worse, there are practical problems in estimating the parameters of mixture models, usually due to insufficient numbers of relevance judgements or quality of them (biases, incompleteness). Approaches which do not use relevance judgements seem difficult to tune, especially when relevance is sparse. Test collections are usually made in such ways that there is some minimum number of relevant items per request. In reality, given a collection, there can be no relevance for some queries. The same can happen when test collections are split further in order to facilitate distributed retrieval setups. As a result, score distributional approaches to score normalization without reference to relevance may have some merit.

A standard method for score normalization that takes the SD into account is the z-score. Scores are normalized, per topic and engine, to the number of standard deviations that they are higher (or lower) than the mean score: s′ = (s − μ)/σ, where μ is the mean score and σ the standard deviation. z-score seems to assume a non-skewed distribution of scores, where the mean would be a meaningful ‘neutral’ score. As it is well-known, actual SDs are highly skewed and clearly violating the assumption underlying the z-score. Although not very popular in IR, z-score was used with reasonable success in Savoy (2003), Kamps et al. (2005).

8.1 The Fernádez et.al. method

A recent attempt models aggregate SDs of many requests, on per-engine basis, with single distributions (Fernández et al. 2006a, b); this enables normalization of scores to probabilities—albeit not of relevance—comparable across different engines. Per engine, the proposed normalization is

$$ s' = {{F}}^{-1}( P(S\le s) ) $$
(1)

where P(S ≤ s) is the cumulative density function (CDF) of the probability distribution of all scores aggregated by submitting a number of queries to the engine, and F is the CDF of “the score distribution of an ideal scoring function that matches the ranking by actual relevance”. The F −1 transformation is called “standardization step”, it is common across all engines participating in a fusion or distributed setup, and considered critical to the method for compensating for potential individual system biases.

In a large fusion experiment using TREC Web Track data, Fernández et al. (2006a, b) found that the method performs better than CombSUM (with standard or rank-sim normalization) and CombMNZ (Lee 1997). For score aggregation, historical queries were used, and only 25–50 seemed enough for good end-results. The method seems very promising, however, unnecessary complicated as we explain next.

8.2 The aggregate historical CDF method

By definition, F is monotonically increasing since it is a CDF. Its quantile function F −1 is also monotonically increasing, and since it is applied as a constant transformation to all engines it has no effect on rankings or the comparability of normalized scores across engines. Thus, at least in distributed retrieval setups where normalized ranked lists are simply merged, F −1 has no impact and it can safely be removed from the calculation. However, F −1 can make a difference if the resulting scores are going to be linearly combined, as e.g. in meta-search/fusion setups, because it is non-linear. Nevertheless, its impact and interpretation is unclear.

The distribution in question is roughly approximated by the “average distribution of several good scoring systems”, not a very well-defined concept. The transformation seems to be an attempt to turn the probability back into something that looks a little more like a score, so that it can be operated on as if it were a score—for example, summed with other scores.

Consequently, we find it hard to see why the combination of functions in Eq. 1 returns a meaningful number, and since F −1 is constant across engines we could settle for the simpler method

$$ HIS: \quad s' = P(S_{HIS}\le s) $$
(2)

where his refers to the fact that historical queries are used for aggregating the SD that the random variable S HIS follows. his normalizes input scores s to the probability of a historical query scoring at or below s. The aggregate historical SD is an average which can be seen as produced by an ‘average’ historical query. In this respect, his normalizes the SD of the ‘average’ query to uniform in [0,1]. Cormack et al. (1999) takes a similar approach, by averaging the distribution over queries; see also the discussion in Hawking and Robertson (2003).

8.3 Signal-to-noise methods

The his method was found to be very robust and well-performing score normalization method in distributed retrieval (Arampatzis and Kamps 2009). The same study went further to suggest normalization methods based on the assumption that scores consist of a signal and a noise component. The distributions of signal and noise over scores were approximated by submitting appropriate sets of artificial queries to each participating search engine, in a similar fashion to the his method. These signal-to-noise methods are essentially dual distribution methods without reference to relevance, and they were found to perform better than his. We will not expand further here but refer the reader to the last-cited study.

8.4 Caveats

With the exception of z-score, the single distribution approaches we analyzed above characterize an engine with a single score transfer function. The underlying implicit assumption for doing that, instead of doing it per query as mixture models do, is that systems produce scores comparable across queries. It is possible, however, that a system’s scores are affected by query characteristics independent of relevance (e.g. query length, sum of query term IDFs, etc.)

The notion of whether or not scores are comparable across queries is a somewhat complex one. For example, one may argue that any scoring function that involves a linear sum of term weights must yield scores which are not comparable across queries, because it clearly can get larger with more terms in the query. But that is not necessarily a good argument—if what is needed is a probability of relevance, then it may simply be that with a longer query one can assign a higher probability of relevance to some documents. As another example, BM25 has a much more subtle dependence on the query—arising from the fact that it ignores the prior probability of relevance (because it does not affect the per-query ranking)—so that the scores for queries with many or few relevants in total should not be comparable. Consequently, there are all sorts of reasons to doubt score comparability across queries.

The single SD approaches analyzed above cannot introduce non-convexity since they do not affect ranking order; they are monotonic transformations of the input score. But even if they perform better than mixture models in some setups, e.g. where a particular mixture does not fit well or relevance is sparse making fitting the relevant component distribution difficult, they are (with the exception of z-score) based on the dubious assumption of score comparability across queries. Thus, they may not be theoretically sound. In practice, the problem can be dealt with by profiling SDs in ranges of values of affecting query features. This, however, opens up many questions such as which the affecting features are, what their suitable value ranges are, etc., and possibly introduces many parameters by increasing the dimensionality of the problem.

At any rate, the aggregate SD methods may be computationally expensive but practically feasible and efficient, since transfer functions can be pre-calculated offline and may only have to change with significant collection updates. Nevertheless, it is not clear—if it is even possible—how using a single SD or z-score can be applied to thresholding, where for optimizing most common measures a reference to (or probabilities of) relevance are needed.

9 Logistic regression

One of the main purposes of the SD analysis is to help to discover a good form of score normalization, preferably one that turns a score into a probability of relevance. An alternative approach would be to attempt to devise new scoring functions that have good distributional properties, or seek a calibration function by trying out different transformations on the scores of an existing system. Following the discussion on independence of Sect. 1, we make a connection with the work of Cooper et al. (1992), who argue that systems should give users explicit probability-of-relevance estimates, and use logistic regression techniques to achieve this. The idea of using logistic regression in this context dates back in Robertson and Bovey (1982), and re-iterated by many others. Footnote 4

Given some training data, logistic regression has been used to calibrate scores in some specific systems, mainly just with a view to ranking (Robertson and Bovey 1982), but partly also to give calibrated probabilities (Cooper et al. 1992; Robertson and Walker 2000; Nottelmann and Fuhr 2003). In Cooper’s approach, it was found necessary to do the regression in two stages, in order to compensate for systematic biases introduced into probabilistic models at the first stage by statistical independence assumptions. However, the model in Cooper et al. (1994) did not fit the data well. In the case of Robertson and Walker, logistic regression was applied to a score produced by BM25, simply in order to calibrate it correctly for thresholding, and it did pretty well in adaptive filtering. Nottelmann and Fuhr compared logistic against linear regression for mapping probabilities of inference to probabilities of relevance in a distributed retrieval context, and found that logistic functions yield better results.

In theory, the scores produced by any system could be calibrated using a combination of logistic regression and well-chosen transformations. Basic logistic regression assumes a linear relationship between the independent variables, in this case the uncalibrated score and log-odds. Thus any non-linearity in this relationship would have to be dealt with by an initial transformation of the independent variable. Appropriate transformations might need to be guessed (this is potentially a disadvantage of this method) or perhaps investigated using a technique such as that discussed in Craswell et al. (2005). An advantage would be that any dependence of the scores on query features such as length could potentially be taken account of, by including such features as additional independent variables. The result of this process would be a normalised score, either as log-odds on a (−∞, ∞) scale or as a probability in a (0,1) range.

This approach is non-parametric—that is, it is not dependent on any assumptions about or analysis of score distributions. In effect, the role played by distributional assumptions in the other methods discussed here is taken over by the transformations question. However, it is not applicable if there are no training data, and the coefficients estimated depend heavily on the choice of the training sample (Fuhr et al. 1993). Also, while there is some agreement on which query features affect scores and should be taken as independent variables, there are also variations; e.g. Fuhr et al. (1993) use the sums of the logged IDFs of the matched terms while Cooper et al. (1994) use the means.

At any rate, the resulting probabilities of relevance are sufficient for merging rankings in distributed retrieval and fusion setups, and for some of the thresholding tasks identified in the introduction but not for all—some require more complete distributional information. Given probabilities of relevance, however, we may find it easier to perform SD analysis and the chances of discovering a universal pair of distributions greater. Thus, logistic regression, or some other transformation, may play a calibrating role helping out in further distributional analysis. This is an under-explored avenue worth pursuing.

10 Conclusions and directions for future research

The empirical evidence so far confirm that SD methods are effective for thresholding in filtering or ranked lists, as well as score normalization in meta-search. Specifically, the normal-exponential model seems to fit best vector space or geometric and BM25 retrieval models. Some mixtures have theoretical problems with an unclear practical impact. For example, the impact of non-convexity of the normal-exponential model on thresholding seems insignificant, however, elsewhere the effect may vary. Latest improvements of the model, namely, using truncated component densities alleviate the non-convexity problem—providing also better fits on data and better end-effectiveness in thresholding—without eliminating it (Arampatzis et al. 2009).

The classic methods assume a binary relevance. A different approach would have to be taken, if degrees of relevance are assumed. For example, in TREC Legal 2008, there was a 3-way classification into non-relevant, relevant, and highly relevant. This complicates the analysis considerably, suggesting the need for three distributions. In this respect, it would fit more naturally with a model where both or all distributions came from the same family. It is difficult to see how one could adapt something like the normal-exponential combination to this situation. However, the recently-proposed model of n-normals-gamma (Kanoulas et al. 2009) may provide a starting point. On the flip-side, approaches that analyze SDs without reference to relevance are just beginning to spring up (Fernández et al. 2006a, b; Arampatzis and Kamps 2009); although effective for score normalization in distributed IR and seemingly suitable for fusion, they seem unsuitable for thresholding tasks.

An alternative approach to the modeling problem would be to attempt to devise new scoring functions that have good distributional properties, or seek a calibration function by trying out different transformations on the scores of an existing system. These could be achieved by means of logistic regression producing probabilities of relevance. Probability of relevance itself is sufficient for the tasks of distributed retrieval and fusion and for some of the thresholding tasks identified in the introduction but not for all—some require more complete distributional information. However, given probabilities of relevance we may find it easier to perform SD analysis and the chances of discovering a universal pair of distributions greater.

A universal pair should satisfy some conditions from an IR perspective. Although the two new hypotheses we introduced do not seem to align their demands with each other or with the older one, the pair that seems more ‘bullet-proof’ is that of the two gamma suggested by Baumgarten (1999). The gamma can also become normal via a GCL or exponential via k = 1, thus allowing for the two exponential and normal-exponential combinations which are also likely depending on which conditions/hypotheses one considers. The increased degrees of freedom offered by the two gamma, however, is a two-edged sword: it may just allow too much. Parameter estimation methods introduce another layer of complexity, approximations, and new problems, as voiced by most previous experimental studies and more recently by Arampatzis and Kamps (2008). At any rate, the distributions in question do not necessarily have to be known ones.