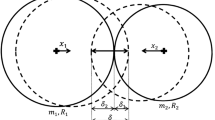
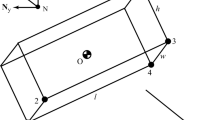
Different models of a perfectly inelastic collision of rigid bodies in plane motion are compared. Formulas for the impact impulses are derived for the Kane–Levinson–Whittaker model based on the kinematic restitution factor, the Routh model based on the kinetic restitution factor, and the Stronge model based on the energy restitution factor. It is shown that these formulas coincide if the collision of rough rigid bodies in plane motion is perfectly inelastic
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
N. V. Butenin, Ya. L. Lunts, and D. R. Merkin, Course of Theoretical Mechanics [in Russian], Vol. 2, Nauka, Moscow (1979).
N. N. Bukhgol’ts, Basic Course in Theoretical Mechanics [in Russian], Part 2, Nauka, Moscow (1966).
V. F. Zhuravlev, Fundamentals of Theoretical Mechanics [in Russian], Fizmatlit, Moscow (2001).
A. P. Ivanov, Dynamics of Systems Undergoing Mechanical Impacts [in Russian], Mezhd. Progr. Obraz., Moscow (1997).
V. V. Kosarchuk and A. V. Agarkov, “Predicting the life of rails based on a contact fatigue crack initiation criterion,” DETUT, Ser. Tekhn. Tekhnol., 20, 77–90 (2012).
Ya. G. Panovko, An Introduction to the Theory of Mechanical Shock [in Russian], Nauka, Moscow (1977).
G. Gilardi and I. Sharf, “Literature survey of contact dynamics modeling,” Mechanism and Machine Theory, 37, 1213–1239 (2002).
W. Goldsmith, Impact: The Theory and Physical Behavior of Colliding Solids, Edward Arnold London (1960).
T. T. Kane and D. A. Levinson, Dynamics. Theory and Applications, McGraw-Hill New York (2005).
V. D. Kubenko, “Stress state of an elastic half-plane under nonstationary loading,” Int. Appl. Mech., 51, No. 2, 121–129 (2015).
V. B. Larin, “Algorithms for solving a unilateral quadratic matrix equation and the model updating problem,” Int. Appl. Mech., 50, No. 3, 321–334 (2014).
A. A. Martynyuk and N. V. Nikitina, “On periodic motion in three-dimensional systems,” Int. Appl. Mech., 51, No. 4, 369–379 (2015).
N. P. Plakhtienko, “Translation of a rigid body with gravity–friction seismic dampers,” Int. Appl. Mech., 45, No. 7, 786–796 (2009).
E. J. Routh, Dynamics of a System of Rigid Bodies, Edward Arnold London (1860).
W. J. Stronge, Impact Mechanics, Cambridge University Press, Cambridge (2000).
W. J. Stronge, “Unraveling paradoxical theories for rigid body collisions,” ASME J. Appl. Mech., 58, No. 4, 1049–1055 (1991).
E. T. Whittaker, A Treatise on the Analytical Dynamics of Particles and Rigid Bodies, Cambridge University Press, Cambridge (1917).
Author information
Authors and Affiliations
Corresponding author
Additional information
Translated from Prikladnaya Mekhanika, Vol. 52, No. 5, pp. 137–144, September–October, 2016.
Rights and permissions
About this article
Cite this article
Zabuga, A.G. Modeling the Collision with Friction of Rigid Bodies. Int Appl Mech 52, 557–562 (2016). https://doi.org/10.1007/s10778-016-0776-0
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10778-016-0776-0