Skip to main content
SpringerLink
Log in

Exact Solution of Some Axisymmetric Problems for Elastic Cylinders of Finite Length Taking Into Account Specific Weight

  • Published:
International Applied Mechanics Aims and scope

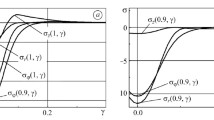
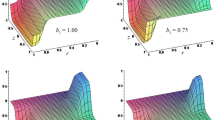
The finite Hankel transform is used to find the exact solution of two axisymmetric problems of elasticity for solid and hollow cylinders of finite length taking their specific weight into account. The boundary conditions at the lower end and on the lateral faces of the cylinders are sliding restraint. Axisymmetric normal and tangential forces act on the upper end. The transforms of the displacements and stresses are obtained. The calculated normalized stresses on the outside and inside cylindrical surfaces are plotted for different height ratios

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Similar content being viewed by others

References

  1. B. L. Abramyan and A. Ya. Aleksandrov, “An axisymmetric problem of elasticity,” in: Proc. 2nd All-Union Congr. on Theoretical and Applied Mechanics [in Russian], Issue 3, Nauka, Moscow (1966), pp. 7–37.

  2. G. N. Bukharinov, “Revisiting the problem of the equilibrium of an elastic circular cylinder,” Vestn. Leningrad. Univ., No. 2, 3–23 (1952).

  3. A. N. Guz and Yu. N. Nemish, Statics of Noncanonical Elastic Bodies in Vol. 2 of the six-volume series Three-Dimensional Problems in Elasticity and Plasticity [in Russian], Naukova Dumka, Kyiv (1984).

  4. O. O. Kapshivyi, “Applying p-analytic functions in an axisymmetric problem of elasticity,” Visn. Kyiv. Univ., Ser. Mat. Mekh., 1, No. 5, 76–89 (1962).

  5. M. A. Koltunov, Yu. N. Vasil’ev, and V. A. Chernykh, Elasticity and Strength of Cylindrical Bodies [in Russian], Vysshaya Shkola, Moscow (1975).

  6. G. Ya. Popov, “A method of integral transforms applied to find the exact solutions of boundary-value problems of mathematical physics,” Mat. Met. Fiz.-Mekh. Polya, 46, No. 3, 74–89 (2003).

  7. G. Ya. Popov, “Axisymmetrical boundary-value problems of elasticity theory for finite-length cylinders and cones,” Dokl. Phys., 56, No. 7, 407–412 (2011).

  8. G. Ya. Popov and Yu. S. Protserov, “Axisymmetric problem for an elastic cylinder of finite length with clamped lateral surface under gravity,” Mat. Met. Fiz.-Mekh. Polya, 57, No. 1, 57–68 (2014).

  9. M. Abramowitz and I. A. Stegun (eds.), Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, Dover, New York (1972).

    MATH  Google Scholar 

  10. E. Jahnke, F. Emde, and F. Losch, Tafeln hoherer Funktionen, B. G. Teubner Verlagsgesellschaft, Stuttgart (1960).

  11. H. Bateman and A. Erdelyi, Higher Transcendental Functions, Vol. 2: Bessel Functions, Parabolic Cylinder Functions and Orthogonal Polynomial, McGraw-Hill, New York (1953).

  12. K. T. Chau and X. C. Wei, “Finite solid circular cylinders subjected to arbitrary surface load. Part I. Analytic solution,” Int. J. Solids Struct., 37, No. 40, 5707–5732 (2000).

    Article  MATH  Google Scholar 

  13. S. D. Conte, K. Z. Miller, and C. B. Sensenig, “The numerical solution of axisymmetric problems in elasticity,” Ballist. Missile Space Techn., No. 4, 173–202 (1969).

  14. Ya. M. Grigorenko and A. Ya. Grigorenko, “Static and dynamic problems for anisotropic inhomogeneous shells with variable parameters and their numerical solution (review),” Int. Appl. Mech., 49, No. 2, 123–197 (2013).

  15. Ya. M. Grigorenko and L. S. Rozhok, “Applying discrete Fourier series to solve problems of the stress state of hollow noncircular cylinders,” Int. Appl. Mech., 50, No. 2, 105–127 (2014).

  16. V. V. Meleshko, “Equilibrium of an elastic finite cylinder. Filon’s problem revisited,” J. Eng. Math., 40, 355–376 (2003).

    Article  MathSciNet  Google Scholar 

  17. G. Ya. Popov, “New transforms for the resolving equations in elastic theory and new integral transforms, with applications to boundary-value problems of mechanics,” Int. Appl. Mech., 39, No. 12, 1400 – 1424 (2003).

  18. V. P. Revenko, “Investigation of the stress–strain state of a finite cylinder under the action of compressive forces,” Mater. Sci., 46, No. 3, 330–335 (2010).

    Article  Google Scholar 

  19. T. A. Vasil’ev and V. A. Shaldyrvan, “Local stress singularities in mixed axisymmetric problems of the bending of circular cylinders,” Int. Appl. Mech., 48, No. 2, 176–187 (2012).

    Article  MATH  MathSciNet  ADS  Google Scholar 

  20. X. X. Wei and K. T. Chan, “Three-dimensional analytical solution for finite circular cylinders subjected to indirect tensile test,” Int. J. Solids Struct., 50, No. 14, 2395–2406 (2000).

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. I. I. Mechnikov Odessa National University, 2 Dvoryanskaya St, Odessa, Ukraine, 65082

    G. Ya. Popov, Yu. S. Protserov & I. A. Gonchar

Authors
  1. G. Ya. Popov
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yu. S. Protserov
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. I. A. Gonchar
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to G. Ya. Popov.

Additional information

Translated from Prikladnaya Mekhanika, Vol. 51, No. 4, pp. 31–44, July–August 2015.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Popov, G.Y., Protserov, Y.S. & Gonchar, I.A. Exact Solution of Some Axisymmetric Problems for Elastic Cylinders of Finite Length Taking Into Account Specific Weight. Int Appl Mech 51, 391–402 (2015). https://doi.org/10.1007/s10778-015-0699-1

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10778-015-0699-1

Keywords

Search

Navigation