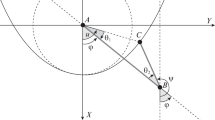
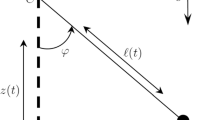
The equation of in-plane vertical motion of a double pendulum suspended at some point of a horizontal elastic string is derived using a hybrid model of this mechanical system. The conditions for the asymptotic stability of the stationary motion of the pendulum interacting with the string are established
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Lj. T. Grujic, A. A. Martynyuk, and M. Ribbens-Pavella, Large-Scale Systems Stability under Structural and Singular Perturbations, Springer-Verlag, Berlin (1987).
R. Courant and D. Hilbert, Methods of Mathematical Physics, Vol. 1, Wiley, New York (1989).
D. M. Lila, Sufficient Stability Conditions for Nonstationary Large-Scale Mechanical Systems [in Ukrainian], Author’s Abstract of PhD Thesis in Theoretical Mechanics (01.02.01), Kyiv (2009).
D. M. Lila, Sufficient Stability Conditions for Nonstationary Large-Scale Mechanical Systems [in Ukrainian], PhD Thesis, Kyiv (2009).
A. P. Markeev, Theoretical Mechanics [in Russian], Nauka, Moscow (1990).
L. A. Pars, A Treatise on Analytical Dynamics, Wiley, New York (1965).
A. N. Tikhonov and A. A. Samarskii, Equations of Mathematical Physics [in Russian], Izd. MGU, Moscow (2004).
I. Z. Shtokalo, “(In)stability criterion for the solutions of linear differential equations with quasi-periodic coefficients,” Mat. Sb., 19 (61), No. 2, 263–286 (1946).
I. Z. Shtokalo, Linear Differential Equations with Variable Coefficients, Gordon & Breach, New York (1961).
A. A. Burov, “Planar motion of an orbital pendulum with periodically oscillating point of suspension,” Cosmic Research, 45, No. 2, 167–169 (2007).
A. Y. T. Leung and J. L. Kuang, “On the chaotic dynamics of a spherical pendulum with a harmonically vibrating suspension,” Nonlin. Dynam., 43, No. 3, 213–238 (2006).
D. M. Lila, “Stability of motion of quasiperiodic systems in critical cases,” Int. Appl. Mech., 46, No. 2, 229–240 (2010).
D. M. Lila, “Stability of some solutions of phase-matched generation equations for optically coupled lasers,” Int. Appl. Mech., 45, No. 3, 317–318 (2009).
D. M. Lila and A. A. Martynyuk, “Construction and applications of the matrix-valued Liapunov functions for some quasi-periodic systems,” Diff. Eqs. Dynam. Syst., 17, No. 1–2, 91–104 (2009).
D. M. Lila and A. A. Martynyuk, “On stability of some solutions for equations of locked lasing of optically coupled lasers with periodic pumping,” Nonlin. Oscill., 12, No. 4, 464–473 (2009).
D. M. Lila and A. A. Martynyuk, “On the theory of stability of matrix differential equations,” Ukr. Math. J., 61, No. 4, 556–565 (2009).
D. M. Lila and A. A. Martynyuk, “Setting up Lyapunov functions for the class of systems with quasiperiodic coefficients,” Int. Appl. Mech., 44, No. 12, 1421–1429 (2008).
D. M. Lila and A. A. Martynyuk, “Stability of periodic motions of quasilinear systems,” Int. Appl. Mech., 44, No. 10, 1161–1172 (2008).
A. A. Martynyuk, Stability of Motion. The Role of Multicomponent Liapunov Functions, Cambridge Sci. Publ., Cambridge (2007).
Author information
Authors and Affiliations
Corresponding author
Additional information
Translated from Prikladnaya Mekhanika, Vol. 46, No. 12, pp. 110–122, December 2010.
Rights and permissions
About this article
Cite this article
Lila, D.M. Stability of the stationary motion of a double pendulum interacting with a string. Int Appl Mech 46, 1428–1439 (2011). https://doi.org/10.1007/s10778-011-0437-2
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10778-011-0437-2