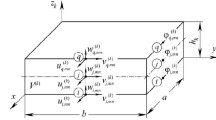
A new approach is followed to study the effect of mixed mechanical boundary conditions on the effectiveness of active damping of the forced resonant vibrations of thermoviscoelastic orthotropic plates. The problem is solved by the Bubnov–Galerkin method. Formulas for the voltage that should be applied to the actuator to damp the first vibration mode are derived. It is shown that the mechanical boundary conditions, the dissipative properties of the material, and the dimenstions of the sensors and actuators have a strong effect on the effectiveness of active damping of the vibrations of plates
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
V. G. Karnaukhov and V. V. Mikhailenko, Nonlinear Thermomechanics of Piezoelectric Inelastic Bodies under Monoharmonic Loading [in Russian], ZhGTU, Zhitomir (2005).
T. V. Karnaukhova, “Active damping of vibrations of plates subject to unknown pressure,” Int. Appl. Mech., 46, No. 5, 562–566 (2010).
T. V. Karnaukhova, “Damping the vibrations of a clamped plate using the sensor’s readings,” Int. Appl. Mech., 46, No. 6, 683–686 (2010).
U. Gabbert and H. S. Tzou, Smart Structures and Structronic Systems, Kluwer, Dordrecht–Boston–London (2001).
T. V. Karnaukhova and E. V. Pyatetskaya, “Basic relations for thermoviscoelastic plates with distributed actuators under monoharmonic loading,” Int. Appl. Mech., 45, No. 2, 200–214 (2009).
T. V. Karnaukhova and E. V. Pyatetskaya, “Damping the resonant flexural vibration of a hinged plate with actuators,” Int. Appl. Mech., 45, No. 4, 448–456 (2009).
T. V. Karnaukhova and E. V. Pyatetskaya, “Damping the flexural vibration of a clamped viscoelastic rectangular plate with piezoelectric actuators,” Int. Appl. Mech., 45, No. 5, 546–557 (2009).
T. V. Karnaukhova and E. V. Pyatetskaya, “Basic relations of the theory of thermoviscoelastic plates with distributed sensors,” Int. Appl. Mech., 45, No. 6, 660–669 (2009).
T. V. Karnaukhova and E. V. Pyatetskaya, “Resonant vibrations of a hinged viscoelastic rectangular plate,” Int. Appl. Mech., 45, No. 7, 762–771 (2009).
J. Tani, T. Takagi, and J. Qiu, “Intelligent material systems: Applications of functional materials,” Appl. Mech. Rev., 51, 505–521 (1998).
H. S. Tzou and L. A. Bergman, Dynamics and Control of Distributed Systems, Cambridge Univ. Press, Cambridge (1998).
Author information
Authors and Affiliations
Corresponding author
Additional information
Translated from Prikladnaya Mekhanika, Vol. 46, No. 9, pp. 71–74, September 2010.
Rights and permissions
About this article
Cite this article
Karnaukhova, T.V. Active damping of the vibrations of a plate using sensor data: effect of boundary conditions. Int Appl Mech 46, 1027–1030 (2011). https://doi.org/10.1007/s10778-011-0394-9
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10778-011-0394-9