Skip to main content
SpringerLink
Log in

Plane instability problem for a composite reinforced with a periodic row of short parallel fibers

  • Published:
International Applied Mechanics Aims and scope

Abstract

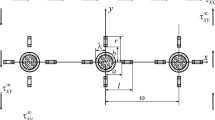
The instability of a composite material reinforced with a periodic row of parallel short fibers is studied considering the interaction of neighboring fibers. Emphasis is on the mutual influence of short fibers in the matrix during loss of stability, depending on the distance between them. A piecewise-homogeneous medium model and the three-dimensional linearized theory of stability of deformable bodies are used

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. I. V. Zolotukhin, “Carbon nanotubes,” Sorosovsk. Obraz. Zh., No. 3, 111–115 (1999).

  2. M. L. Kerber, “Composite materials,” Sorosovsk. Obraz. Zh., No. 5, 33–41 (1999).

  3. A. N. Guz, Fundamentals of the Three-Dimensional Theory of Stability of Deformable Bodies, Springer-Verlag, Berlin-Heilberg (1999).

    MATH  Google Scholar 

  4. A. N. Guz, “Constructing the three-dimensional theory of stability of deformable bodies,” Int. Appl. Mech., 37, No. 1, 1–37 (2001).

    Article  Google Scholar 

  5. A. N. Guz, “Three-dimensional theory of stability of a carbon nanotube in a matrix,” Int. Appl. Mech., 42, No. 1, 19–31 (2006).

    Article  MathSciNet  Google Scholar 

  6. A. N. Guz and V. A. Dekret, “Interaction of two parallel short fibers in the matrix at loss of stability,” Computer Modeling in Engineering & Sciences, 13, No. 3, 165–170 (2006).

    Google Scholar 

  7. A. N. Guz, V. A. Dekret, and Yu. V. Kokhanenko, “Planar stability problem of composite weakly reinforced by short fibers,” Mech. Adv. Mater. Struct., 12, 313–317 (2005).

    Article  Google Scholar 

  8. A. N. Guz and I. A. Guz, “On models in the theory of stability of multiwalled carbon nanotubes in matrix,” Int. Appl. Mech., 42, No. 6, 617–628 (2006).

    Article  MathSciNet  Google Scholar 

  9. A. N. Guz, A. A. Rodger, and I. N. Guz, “Developing a compressive failure theory for nanocomposites,” Int. Appl. Mech., 41, No. 3, 3–37 (2005).

    Article  Google Scholar 

  10. A. N. Guz, J. J. Rushchitsky, and I. A. Guz, “Establishing fundamentals of the mechanics of nanocomposites,” Int. Appl. Mech., 43, No. 3, 247–271 (2007).

    Article  Google Scholar 

  11. V. A. Dekret, “Two-dimensional buckling problem for a composite reinforced with a periodic row of collinear short fibers,” Int. Appl. Mech., 42, No. 6, 684–691 (2006).

    Article  Google Scholar 

  12. Yu. V. Kokhanenko, “Numerical study of three-dimensional stability problems for laminated and ribbon-reinforced composites,” Int. Appl. Mech., 37, No. 3, 317–345 (2001).

    Article  MathSciNet  Google Scholar 

  13. G. M. Odegard, V. M. Harik, K. E. Wise, and T. S. Gates, Constitutive Modeling of Nanotube-Reinforced Polymer Composite Systems, Technical Report, NASA-2001-tm 211044 (2001).

  14. S. P. Xiao and W. Y. Hou, “Fracture of vacancy-defected carbon nanotubes and their embedded nanocomposites,” Physical Review, B73, 115406, 415–406 (2006).

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. S. P. Timoshenko Institute of Mechanics, National Academy of Sciences of Ukraine, Kyiv, Ukraine

    V. A. Dekret

Authors
  1. V. A. Dekret
    View author publications

    You can also search for this author in PubMed Google Scholar

Additional information

__________

Translated from Prikladnaya Mekhanika, Vol. 44, No. 5, pp. 22–31, May 2008.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Dekret, V.A. Plane instability problem for a composite reinforced with a periodic row of short parallel fibers. Int Appl Mech 44, 498–504 (2008). https://doi.org/10.1007/s10778-008-0062-x

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10778-008-0062-x

Keywords

Search

Navigation