Skip to main content
SpringerLink
Log in

Stabilization of a wheeled robotic vehicle

  • Published:
International Applied Mechanics Aims and scope

Abstract

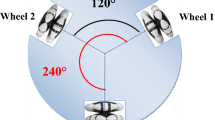
The paper addresses the problem of synthesizing a stabilization system for a robotic vehicle with two steerable wheels with allowance for dynamic effects. A solution is presented for the case of coasting. The general case of stabilization where dynamic effects are taken into account is examined

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. H. Kwakernaak and R. Sivan, Linear Optimal Control Systems, Wiley, New York (1972).

    MATH  Google Scholar 

  2. V. B. Larin, “On stabilization of motions of system with nonholonomic constraints,” J. Autom. Inform. Sci., 38, No. 4, 8–22 (2006).

    Article  MathSciNet  Google Scholar 

  3. A. M. Bloch, Nonholonomic Mechanics and Control, Springer-Verlag, New York (2003).

    MATH  Google Scholar 

  4. A. M. Bloch, M. Reyhanoglu, and A. McClamroch, “Control and stabilization of nonholonomic dynamic systems,” IEEE Trans., Automat. Control, 37, No. 11, 1746–1757 (1992).

    Article  MATH  MathSciNet  Google Scholar 

  5. Fazal-ur-Rehman, “Steering of nonholonomic mobile robots by using differential geometric approach,” Appl. Comp. Math., 1, No. 2, 131–141 (2002).

    MathSciNet  Google Scholar 

  6. V. B. Larin, “Motion planning for a wheeled robot (kinematic approximation),” Int. Appl. Mech., 41, No. 2, 187–196 (2005).

    Article  Google Scholar 

  7. V. B. Larin, “Control of wheeled robots,” Int. Appl. Mech., 41, No. 4, 441–448 (2005).

    Article  MathSciNet  Google Scholar 

  8. V. B. Larin, “Motion planning for a mobile robot with two steerable wheels,” Int. Appl. Mech., 41, No. 5, 552–559 (2005).

    Article  MathSciNet  Google Scholar 

  9. V. B. Larin, “Motion planning in the presence of nonholonomic constraints,” Int. J. Appl. Math. Mech., 2, 96–108 (2005).

    Google Scholar 

  10. V. B. Larin, “Stabilization of a wheeled robotic vehicle subject to dynamic effects,” Int. Appl. Mech., 41, No. 9, 1061–1070 (2006).

    Article  Google Scholar 

  11. R. M. Murray and S. S. Sastry, “Nonholonomic motion planning: Steering using sinusoids,” IEEE Trans., Automat. Control, 38, No. 5, 700–716 (1993).

    Article  MATH  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. S. P. Timoshenko Institute of Mechanics, National Academy of Sciences of Ukraine, Kyiv

    V. B. Larin

Authors
  1. V. B. Larin
    View author publications

    You can also search for this author in PubMed Google Scholar

Additional information

__________

Translated from Prikladnaya Mekhanika, Vol. 43, No. 7, pp. 114–124, July 2007.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Larin, V.B. Stabilization of a wheeled robotic vehicle. Int Appl Mech 43, 800–808 (2007). https://doi.org/10.1007/s10778-007-0081-z

Download citation

  • Received:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10778-007-0081-z

Keywords

Search

Navigation