Skip to main content
SpringerLink
Log in

Three-dimensional stability of a rectangular plate under uniaxial tension

  • Published:
International Applied Mechanics Aims and scope

Abstract

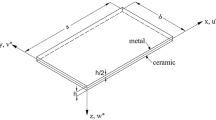
The paper studies the three-dimensional stability of an isotropic, linear elastic, rectangular plate under a uniform tensile load applied to its sides. The concept of free strains is used to reduce the three-dimensional problem to a two-dimensional one. It is solved using the three-dimensional linearized theory of stability. An approximate solution of the buckling problem is obtained by the finite-difference method. Numerical results are presented

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. N. M. Belyaev, Resistance of Materials [in Russian], Nauka, Moscow-Leningrad (1949).

    Google Scholar 

  2. A. N. Guz, Fundamentals of the Three-Dimensional Theory of Stability of Deformable bodies [in Russian], Vyshcha Shkola, Kyiv (1986).

    Google Scholar 

  3. I. N. Molchanov, A. V. Popov, and A. N. Khimich, “Algorithm to solve the partial eigenvalue problem for large profile matrices,” Cybern. Syst. Anal., 28, No. 2, 281–286 (1992).

    Article  MathSciNet  MATH  Google Scholar 

  4. E. Yu. Gladun, A. N. Guz, and Yu. V. Kokhanenko, “Estimating the error of the beam approximation in the plate stability problem for a rectangular plate with a central crack,” Int. Appl. Mech., 40, No. 11, 1290–1296 (2004).

    Article  Google Scholar 

  5. A. N. Guz, “On two-scale model of fracture mesomechanics of composites with cracks under compression, ” Int. Appl. Mech., 41, No. 5, 582–585 (2005).

    Article  MathSciNet  Google Scholar 

  6. A. N. Guz and V. N. Chekhov, “On the determination of loads upon the ground support in underground mine workings,” Int. Appl. Mech., 41, No. 11, 1239–1245 (2005).

    Article  Google Scholar 

  7. Yu. V. Kokhanenko, “Edge effect in a sandwich plate: A plane problem,” Int. Appl. Mech., 40, No. 12, 1411–1418 (2004).

    Article  Google Scholar 

  8. Yu. V. Kokhanenko, “Plane problem of three-dimensional stability for a hinged plate with two symmetric end cracks,” Int. Appl. Mech., 41, No. 4, 381–385 (2005).

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. S. P. Timoshenko Institute of Mechanics, National Academy of Sciences of Ukraine, Kyiv

    Yu. V. Kokhanenko

Authors
  1. Yu. V. Kokhanenko
    View author publications

    You can also search for this author in PubMed Google Scholar

Additional information

__________

Translated from Prikladnaya Mekhanika, Vol. 42, No. 7, pp. 116–123, July 2006.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Kokhanenko, Y.V. Three-dimensional stability of a rectangular plate under uniaxial tension. Int Appl Mech 42, 825–831 (2006). https://doi.org/10.1007/s10778-006-0151-7

Download citation

  • Received:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10778-006-0151-7

Keywords

Search

Navigation