Abstract
Quantum teleportation is the protocol of transmitting quantum states without physically moving them. After the proposal for the first scheme of quantum teleportation in 1993, different schemes have been proposed, according to the application required. In this paper, a new quantum teleportation protocol is proposed for an arbitrary number of users. First, an initial entangled stated made of n + 1 qubits is distributed between the sender and n users. In each run, the sender decides which user is the receiver of the transmitted state. The receiver can retrieve the sent state with the collaboration of the other users. The applications of this protocol are in quantum networks, cloud computing and also quantum cryptography.
Similar content being viewed by others
References
Bennett, C.H., Brassard, G., Crépeau, C., Jozsa, R., Peres, A., Wootters, W.K.: Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels. Phys. Rev. Lett. 70(13), 1895–1899 (1993)
Bouwmeester, D., Pan, J.W., Mattle, K., Eibl, M., Weinfurter, H., Zeilinger, A.: Experimental quantum teleportation. Nature. 390. 80(6), 575 (1997)
Furusawa, A., Sørensen, J.L., Braunstein, S.L., Fuchs, C.A., Kimble, H.J., Polzik, E.S.: Unconditional quantum teleportation. 282(5389), 706–709 (1998)
Nielsen, M.A., Knill, E., Laflamme, R.: Complete quantum teleportation using nuclear magnetic resonance. Nature. 396(6706), 52 (1998)
Karlsson, A., Bourennane, M.: Quantum teleportation using three-particle entanglement. Phys. Rev. A. 58, 4394 (1998)
Yang, K., Huang, L., Yang, W., Song, F.: Quantum teleportation via GHZ-like state. Int. J. Theor. Phys. 48(2), 516–521 (2009)
Shi, B.S., Tomita, A.: Teleportation of an unknown state by W state. Phys. Lett. A. 296(Issues), 4–5 (2002)
Tian, D., Tao, Y., Qin, M.: Teleportation of an arbitrary two-qubit state based on the non-maximally four-qubit cluster state. Sci. China, Ser. G. 51(10), 1523–1528 (2008)
Cardoso, W.B.: Teleportation of GHZ-states in QED-Cavities without the explicit Bell-state measurement. Int. J. Theor. Phys. 47, 977–982 (2008)
Yang, C.P., Han, S.: A scheme for the teleportation of multiqubit quantum information via the control of many agents in a network. Phys. Lett. A. 343(4), (2005)
Deng, F.G., Li, C.Y., Li, Y.S., Zhou, H.Y., Wang, Y.: Symmetric multiparty-controlled teleportation of an arbitrary two-particle entanglement. Phys. Rev. A. 72, 022338 (2005)
Wang, Y.H., Song, H.S.: Preparation of partially entangled W state and deterministic multi-controlled teleportation. Opt. Commun. 281(3), (2008)
Wang, X.W., Su, Y.H., Yang, G.J.: Controlled teleportation against uncooperation of part of supervisors. Quantum Inf. Process. 8, 319–330 (2009)
Yin, W.T., Yan, W.Q.: Controlled quantum teleportation with Bell states. Chin. Phys. B. Vol 20. (2011)
Yang, C.P., Chu, S.I., Han, S.: Efficient many-party controlled teleportation of multiqubit quantum information via entanglement. Phys. Rev. A. 70(2), (2004)
Shukla, C., Banerjee, A., Pathak, A.: Bidirectional controlled teleportation by using 5-qubit states: A generalized view. Int. J. Theor. Phys. 52(10), 3790–3796 (2013)
Li, Y.H., Li, X.I., Sang, M.H., Nie, Y.Y., Wang, Z.S.: Bidirectional controlled quantum teleportation and secure direct communication using five-qubit entangled state. Quantum Inf. Process. 12, 3835–3844 (2013)
Duan, Y.J., Zha, X.W.: Bidirectional quantum controlled teleportation via a six-qubit entangled state. Int. J. Theor. Phys. 53, 3780–3786 (2014)
Chen, Y.: Bidirectional controlled quantum teleportation by using five-qubit entangled state. Int. J. Theor. Phys. 53(5), 1454–1458 (2014)
Duan, Y.J., Zha, X.W., Sun, X.M., Xia, J.F.: Bidirectional quantum controlled teleportation via a maximally seven-qubit entangled state. Int. J. Theor. Phys. 53(8), 2697–2707 (2014)
Chen, Y.: Bidirectional quantum controlled teleportation by using a genuine six-qubit entangled state. Int. J. Theor. Phys. 54, 269–272 (2015)
Hong, W.Q.: Asymmetric bidirectional controlled teleportation by using a seven-qubit entangled State. Int. J. Theor. Phys. 55, 384–387 (2016)
Wang, J.W., Shu, L.: Bidirectional quantum controlled teleportation of qubit state via partially entangled GHZ-type states. Int. J. Mod. Phys. B. 29(18), 1550122 (2015)
Zhang, D., Zha, X.W., Li, W., Yu, Y.: Bidirectional and asymmetric quantum controlled teleportation via maximally eight-qubit entangled state. Quantum Inf. Process. 14(10), 3835–3844 (2015)
Sang, M.H.: Bidirectional quantum controlled teleportation by using a seven-qubit entangled state. Int. J. Theor. Phys. 55, 380–383 (2016)
Hassanpour, S., Houshmand, M.: Bidirectional quantum controlled teleportation by using EPR states and entanglement swapping. In: 23th Iranian Conference on Electrical Engineering (ICEE), arXiv:1502.03551 (2015)
Li, Y.H., Nie, L.P., Li, X.L., Sang, M.H.: Asymmetric bidirectional controlled teleportation by using six-qubit cluster state. Int. J. Theor. Phys. 55, 3008–3016 (2016)
Hassanpour, S.H., Houshmand, M.: Bidirectional teleportation of a pure EPR state by using GHZ states. Quantum Inf. Process. 15, 905–912 (2016)
Li, Y.H., Jin, X.M.: Bidirectional controlled teleportation by using nine-qubit entangled state in noisy environments. Quantum Inf. Process. 15, 929–945 (2016)
SadeghiZadeh, M., Houshmand, M., Aghababa, H.: Bidirectional quantum teleportation of a class of n-qubit states by using (2n+2)-qubit entangled states as quantum channel. Int. J. Theor. Phys. 57, 175–183 (2018)
SadeghiZadeh, M., Houshmand, M., Aghababa, H.: Bidirectional teleportation of a two-qubit state by using eight-qubit entangled state as a quantum channel. Int. J. Theor. Phys. 56, 2101–2112 (2017)
Hassanpour, SH., Houshmand, M.: Bidirectional quantum teleportation via entanglement swapping, In: 23th Iranian Conference on Electrical Engineering (ICEE), Print ISSN: 2164–7054 (2015)
Bolokian, M., Sadeghizadeh, M. S., Hooshmand, M.: Simultaneous quantum distribution of a single qubit state to three receivers. Accepted at the 27th National Electricity Conference of Iran, Yazd, (1398)
Ishizaka, S., Hiroshima, T.: Quantum teleportation scheme by selecting one of multiple output ports. Phys. Rev. A. 79(4), 042306 (2009)
Yu, Y., Zha, X.W., Li, W.: Quantum broadcast scheme and multi-output quantum teleportation via four-qubit cluster state. Quantum Inf. Process. 16, 41 (2017)
Nakahara, M., Ohmi, T.: Quantum computing: from linear algebra to physical realizations, CRC Press; International Standard Book number-13:978-1-4200-1229-3, (2008)
Nielsen, M.A., Chuang, I.L.: Quantum computation and quantum information. American Journal of Physics. 70, 558 (2002)
Hillery, M., Vladimír, B., André, B.: Quantum secret sharing. Phys. Rev. A. 59(3), (1999)
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix: Proving the correctness of the protocol
Appendix: Proving the correctness of the protocol
In this section, we prove that the qubit belongs to Bobn according to the result of Alice’s measurement and the number of even / odd values of “-” in the measurements of other users, corresponds to Table 2. Proof is done by mathematical induction. First we prove the correctness of Table 2 for the k = 2 state (minimum number of receivers for this protocol). Then we show that if the table correctness is valid for k = n − 1, then it is also valid for k = n.
1.1 The proof for k = 2
In this section, we rewrite the protocol for dual-receiver mode. Alice first generates the channel used in this protocol as follows.
She then holds the qubit A, sends the qubit B1 to Bob1 and the qubit B2 to Bob2. The complete state of the system (by considering the state |φ⟩A) is as follows:
After applying the CNOT operator on qubit a as the control and qubit A as the target and then applying the Hadamard gate on the qubit a, the state of the system changes as follows.
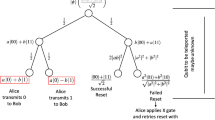
In the third step, Alice measures the two qubits according to computational basis a and A. According to Relation (16), the measurement results and post-measurement states of Bob1 and Bob2 can be seen in Table 4. Alice reveals the result of the measurement on the public channel.
In this step, suppose Bob2 is the receiver of Alice. Bob1 measures its qubit based on the X and declares the result. According to Relations (17) the collapsed stateB2 corresponds to Table 5.
According to Table 5, when the measurement result is “+”, it means that num{−} is an even number, and when it is “-”, it means that num{−} is an odd number, the post-measurement state is according to Table 2.
1.2 Inductive reasoning
Assume that k = n − 1 mode is valid for the correctness of Table 2. Now we prove that for k = n mode, the correctness of Table 2 is also valid. Proof is provided for the case that the result of Alice’s measurement is “00”. For other results, Alice’s measurement is in the same way.
According to the induction assumption, the α| 0〉⊗(n − 1) + β| 1〉⊗(n − 1) state can be written as follows.
Now by adding a user, the post-measurement state of Alice according to Table 1 is in the form of relation (19).
According to Relation (18), The Relation (19) can be written as follows:
Given the equality of Relation (21), which results from Relation (20), the correctness of Table 2 is proved
Rights and permissions
About this article
Cite this article
Bolokian, M., Houshmand, M., Sadeghizadeh, MS. et al. Multi-Party Quantum Teleportation with Selective Receiver. Int J Theor Phys 60, 828–837 (2021). https://doi.org/10.1007/s10773-020-04702-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10773-020-04702-y