Skip to main content
SpringerLink
Log in

Entanglement Properties of the Kerr-Down Conversion System

  • Published:
International Journal of Theoretical Physics Aims and scope Submit manuscript

Abstract

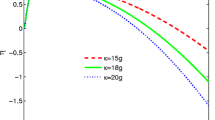
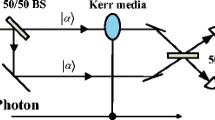
We investigate the entanglement properties of the Kerr-down conversion system with two entanglement criteria. We first obtain the exact analytic solutions for operators under certain condition. Using the exact analytic solutions, we show that the azimuth angle is independence of linear interaction; while the polar angle is independence of nonlinear interaction. By characterizing the degree of entanglement with two criteria, we see that the entanglement properties of the Kerr-down conversion system can be controlled by adjusting the nonlinear interaction and the linear interaction.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2

Similar content being viewed by others

References

  1. Einstein, A., Podolsky, B., Rosen, N.: Phys. Rev. 47, 777 (1935)

    Article  ADS  Google Scholar 

  2. Li, S.-S., Huang, Y.-B.: Int. J. Quant. Infrom. 6, 561 (2008)

    Article  Google Scholar 

  3. Jian, S.: Int. J Theor. Phys. 52, 2851 (2013)

    Article  Google Scholar 

  4. Kraus, B., Büchler, H.P., Diehl, S., Kantian, A., Micheli, A., Zoller, P.: Phys. Rev. A 78, 042307 (2008)

    Article  ADS  Google Scholar 

  5. Unanyan, R.G., Vitanov, N.V., Bergmann, K.: Phys. Rev. Lett. 87, 137902 (2001)

    Article  ADS  Google Scholar 

  6. Marr, C., Beige, A., Rempe, G.: Phys. Rev. A 68, 033817 (2003)

    Article  ADS  Google Scholar 

  7. Shi, B.-S., Tomita, A.: J. Opt. B: Quantum Semiclassical Opt. 4, 380 (2002)

    Article  ADS  MathSciNet  Google Scholar 

  8. Ma, P.-C., Chen, G.-B., Li, X.-W., Zhan, Y.-B.: Laser Phys. 26, 105201 (2016)

    Article  ADS  Google Scholar 

  9. El-Orany, F.A.A., Sebawe Abdalla, M., Peřina, J.: Eur. Phys. J. D 41, 391 (2007)

    Article  ADS  Google Scholar 

  10. Pezzé, L., Smerzi, A.: Phys. Rev. Lett. 102, 100401 (2009)

    Article  ADS  MathSciNet  Google Scholar 

  11. Tóth, G., Knapp, C., Gühne, O., Briegel, H.J.: Phys. Rev. Lett. 99, 250405 (2007)

    Article  ADS  Google Scholar 

  12. Senko, C., Smith, J., Richerme, P., Lee, A., Campbell, W.C., Monroe, H.C.: Science 345, 530 (2014)

    Article  Google Scholar 

  13. Braunstein, S.L., Caves, C.M.: Phys. Rev. Lett. 72, 3439 (1994)

    Article  ADS  MathSciNet  Google Scholar 

  14. Wootters, W.K.: Phys. Rev. D 23, 357 (1981)

    Article  ADS  MathSciNet  Google Scholar 

  15. Jin, G.-R., Liu, Y.-C., Liu, W.-M.: New J. Phys. 11, 073049 (2009)

    Article  ADS  Google Scholar 

  16. Li, S.-S.: Int. J Theor. Phys. 54, 3503 (2015)

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Electronic Commerce, Jiangxi University of Finance and Economics, Nanchang, 330013, People’s Republic of China

    Shu Jian

Authors
  1. Shu Jian
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Shu Jian.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Jian, S. Entanglement Properties of the Kerr-Down Conversion System. Int J Theor Phys 57, 1553–1558 (2018). https://doi.org/10.1007/s10773-018-3680-z

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10773-018-3680-z

Keywords

Search

Navigation