Faithful Pointer for Qubit Measurement

Abstract

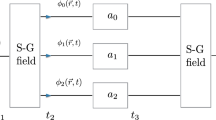
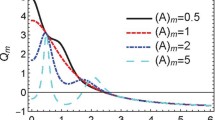
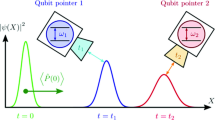
In the context of von Neumann projective measurement scenario for a qubit system, it is widely believed that the mutual orthogonality between the post-interaction pointer states is the sufficient condition for achieving the ideal measurement situation. However, for experimentally verifying the observable probabilities, the real space distinction between the pointer distributions corresponding to post-interaction pointer states play crucial role. It is implicitly assumed that mutual orthogonality ensures the support between the post-interaction pointer distributions to be disjoint. We point out that mutual orthogonality (formal idealness) does not necessarily imply the real space distinguishability (operational idealness), but converse is true. In fact, for the commonly referred Gaussian wavefunction, it is possible to obtain a measurement situation which is formally ideal but fully nonideal operationally. In this paper, we derive a class of pointer states, that we call faithful pointers, for which the degree of formal (non)idealness is equal to the operational (non)idealness. In other words, for the faithful pointers, if a measurement situation is formally ideal then it is operationally ideal and vice versa.