Abstract
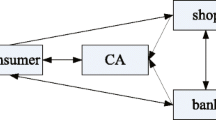
In an arbitrated quantum signature scheme, the signer signs the message and the receiver verifies the signature’s validity with the assistance of the arbitrator. We present an arbitrated quantum blind signature scheme by measuring four-particle cluster states and coding. By using the special relationship of four-particle cluster states, we cannot only support the security of quantum signature, but also guarantee the anonymity of the message owner. It has a wide application to E-payment system, E-government, E-business, and etc.
Similar content being viewed by others
References
Gottesman, D., Chuang, I.: Quantum digital signatures, arXiv:quant-ph/0105032v2 (2001)
Buhrman, H., Cleve, R., Watrous, J., et al.: Quantum fingerprinting. Phys. Rev. Lett. 87, 167902 (2001)
Buhrman, H., Crepeau, C., Gottesman, D., et al.: Authentication of quantum messages. pp. 449–458. IEEE Computer Society Press, Washington DC (2002)
Zeng, G.H., Keitel, C.H.: Arbitrated quantum-signature scheme. Phys. Rev. A 65, 042312 (2002)
Li, Q., Chan, W.H., Long, D.Y.: Arbitrated quantum signature scheme using Bell states. Phys. Rev. A 79, 054307 (2009)
Zou, X.F., Qiu, D.W.: Security analysis and improvements of arbitrated quantum signature schemes. Phys. Rev. A 82, 042325 (2010)
Gao, F., Qin, S.J., Guo, F.Z., Wen, Q.Y.: Cryptanalysis of the arbitrated quantum signature protocols. Phys. Rev. A 84, 022344 (2011)
Choi, J.W., Chang, K.Y., Hong, D.: Security problem on arbitrated quantum signature schemes. Phys. Rev. A 84, 062330 (2011)
Hwang, T., Luo, Y.P., Chong, S.K., Chong S.K.: Comment on: security analysis and improvements of arbitrated quantum signature schemes. Phys. Rev. A 85, 056301 (2012)
Cai, Q.Y.: The “Ping-Pong” Protocol Can Be Attacked without Eavesdropping. Phys. Rev. Lett. 91, 109801 (2003)
Gao, F., Guo, F.Z., Wen, Q.Y., Zhu, F.C.: Consistency of shared reference frames should be reexamined. Phys. Rev. A 77, 014302 (2008)
Gisin, N., Fasel, S., Kraus, B., Zbinden, H.: Ribordy, G.: Trojan-horse attacks on quantum-key-distribution systems. Phys. Rev. A 73, 022320 (2006)
Deng, F.G., Li, X.H., Zhou, H.Y., Zhang, Z.J.: Improving the security of multiparty quantum secret sharing against Trojan horse attack. Phys. Rev. A 72, 044302 (2005)
Zhang, K.J., Qin, S.J., Sun, Y., Song, T.T., Su, Q.: Reexamination of arbitrated quantum signature: The impossible and the possible. Quantum Inf. Proc. 12(7), 3127–3141 (2013)
Zhang, K.J., Li, D., Su, Q.: Security of the arbitrated quantum signature protocols revisited. Phys. Scr. 89, 015102 (2014)
Zhang, K.J., Zhang, W.W., Li, D.: Improving the security of arbitrated quantum signature against the forgery attack. Quantum Inf. Proc. 12(8), 2655–2669 (2013)
Yang, Y.G.: Multi-proxy quantum group signature scheme with threshold shared verification. Chin. Phys. B 17, 415 (2008)
Yang, Y.G., Wen, Q.Y.: Threshold proxy quantum signature scheme with threshold shared verification. Sci. Chin. Ser. G: Phys. Mech. Astron. 51, 1079C1088 (2008)
Yang, Y.G., Wang, Y., Teng, Y.W., Chai, H.P., Wen, Q.Y.: Scalable arbitrated quantum signature of classical messages with multi-signers. Commun. Theor. Phys. 54, 84 (2010)
Yang, Y.G., Wen, Q.Y.: Arbitrated quantum signature of classical messages against collective amplitude damping noise. Opt. Commun. 283, 3198–3201 (2010)
Wang, T. Y., Wen, Q.Y.: Fair quantum blind signatures. Chin. Phys. B 19, 060307 (2010)
Wang, T.Y., Wei, Z.L.: One-time proxy signature based on quantum cryptography. Quantum Inf. Proc. (2012). doi:10.1007/s11128-011-0258-6
Chaum, D.: Elections with unconditionally-secret ballots and disruption equivelent to breaking RAS. Advances in cryptology. In: Proceedings of Euro-Crypto88, p 177C189. Springer, Berlin (1988)
Brands, S.: Untraceble off-line cash in wallet with observers. Advances in cryptology. In: Proceeding of Crypto93, p 302C318. Springer, Berlin (1994)
Wang, T.Y., Cai, X.Q., Zhang, J.Z.: Off-line e-cash system with multiple banks based on elliptic curve. Comput. Eng. Appl. 33(15), 155C157 (2007)
Wen, X.J., Chen, Y.Z., Fang, J.B.: An inter-bank E-payment protocol based on quantum proxy blind signature. Quantum Inf. Process. 12(1), 549C558 (2013)
Cai, X.Q., Wei, C.Y.: Cryptanalysis of an inter-bank E-payment protocol based on quantum proxy blind signature. Quantum Inf. Process. 12(4), 1651C1657 (2013)
Harn, L.: Cryptanalysis of the blind signature based on the discrete logarithm. Electron. Lett. 31(14), 1136C1137 (1995)
Fan, C., Lei, C.: Efficient blind signature scheme based on quadratic residues. Electron. Lett. 32(9), 811C813 (1996)
Briegel, H.J., Raussendorf, R.: Persistent entanglement in arrays of interacting particles. Phys. Rev. Lett. 86(5), 910 (2001)
Shen, D.-S., Ma, W.-P., Wang, L.-l.: Two-party quantum key agreement with four-qubit cluster states. Quantum Inf. Process 13, 2313–2324 (2014)
Shukla, C., Kothari, V., Banerjee, A., Pathak, A.: On the group-theoretic structure of a class of quantum dialogue protocols. Phys. Lett. A 377, 518C527 (2013)
Bennett, C.H., Brassard, G.: Quantum cryptography: public key distribution and coin tossing. In: Proceedings of IEEE international conference on computers, systems, and signal processing, pp. 175–179. IEEE Press, New York (1984)
Ekert, A.K.: Quantum cryptography based on bell theorem. Phys. Rev. Lett. 67, 661–663 (1991)
Bennett, C.H.: Quantum cryptography using any two nonorthogonal states. Phys. Rev. Lett. 68, 3121–3124 (1992)
Bennett, C.H., Brassard, G., et al.: Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels. Phys. Rev. Lett. 70, 1895–1899 (1993)
Gao, F., Guo, F.Z., Wen, Q.Y., et al.: Quantum key distribution without alternative measurements and rotations. Phys. Lett. A 349, 53–58 (2006)
Boykin, P.O., Roychowdhury, V.: Optimal encryption of quantum bits. Phys. Rev. A 67, 042317 (2003)
Gao, F., Guo, F.Z., Wen, Q.Y., Zhu, F.C.: Comment on “Experimental demonstration of a quantum protocol for byzantine agreement and liar detection”. Phys. Rev. Lett. 101, 208901 (2008)
Zhang, Y.S., Li, C.F., Guo, G.C.: Comment on “Quantum key distribution without alternative measurements”. Phys. Rev. A 63, 036301 (2001)
Gao, F., Qin, S.J., Wen, Q.Y., Zhu, F.C.: A simple participant attack on the bradler-dusek protocol. Quantum Inf. Comput. 7, 329 (2007)
Gao, F., Wen, Q.Y., Zhu, F.C.: Teleportation attack on the QSDC protocol with a random basis and order. Chin. Phys. B 17, 3189 (2008)
Gao, F., Qin, S.J., Guo, F.Z., Wen, Q.Y.: Dense-coding attack on three-party quantum key distribution protocols. IEEE J. Quantum Electron. 47, 630 (2011)
Qin, S.J., Gao, F., Wen, Q.Y., Zhu, F.C.: Improving the security of multiparty quantum secret sharing against an attack with a fake signal. Phys. Lett. A 357, 101 (2006)
W’ojcik, A.: Eavesdropping on the Ping-Pong quantum communication protocol. Phys. Rev. Lett. 90, 157901 (2003)
W’ojcik, A.: Comment on “Quantum dense key distribution”. Phys. Rev. A 71, 016301 (2005)
Gao, F., Wen, Q.Y., Zhu, F.C.: Comment on: “Quantum exam”. Phys. Lett. A 360, 748 (2007)
Gao, F., Lin, S., Wen, Q.Y., Zhu, F.C.: A special eavesdropping on one-sender versus N-receiver QSDC protocol. Chin. Phys. Lett. 25, 1561 (2008)
Gao, F., Lin, S., Wen, Q.Y., Zhu, F.C.: Cryptanalysis of multiparty controlled quantum secure direct communication using Greenberger-Horne-Zeilinger state. Opt. Commun. 283, 192 (2010)
Security of quantum digital signatures for classical messages Tian-Yin Wang, Xiao-Qiu Cai, Yan-Li Ren, Rui-Ling Zhang:Security of quantum digital signatures for classical messages. Scientific Reports 5, 9231 (2015)
Wang, T.-Y., Cai, X.-Q., Zhang, R.-L.: Security of a sessional blind signature based on quantum cryptograph. Quantum Inf. Process 13, 1677C1685 (2014)
Cai, X.-Q., Zheng, Y.-H., Zhang, R.-L.: Cryptanalysis of a batch proxy quantum blind signature scheme. Int. J. Theor. Phys. 53, 3109C3115 (2014)
Acknowledgments
This work is supported by NSFC (Grant Nos. 61272057, 61170270), Beijing Higher Education Young Elite Teacher Project (Grant Nos. YETP0475, YETP0477).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Fan, L. A Novel Quantum Blind Signature Scheme with Four-Particle Cluster States. Int J Theor Phys 55, 1558–1567 (2016). https://doi.org/10.1007/s10773-015-2793-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10773-015-2793-x