Abstract
The dynamics of a mixed spin system governed by XXZ model in additional to an intrinsic decoherence is investigated. The behavior of quantum correlation and the degree of entanglement between the two subsystems is quantified by using measurement-induced disturbance and the negativity, respectively. It is shown that, the phenomena of long-lived entanglement appears for larger values of intrinsic decoherence parameters. The degree of entanglement and quantum correlation depend on the dimensions of subsystems which are pass through the external field and the initial states setting. We show that the negativity for some initial classes is more robust than the measurement-induced disturbance, while for some other initial classes the quantum correlations are more robust than entanglement.
Similar content being viewed by others
1 Introduction
Nowadays, correlated systems represent one of the most important partners in the context of quantum communication [1, 2], quantum networks [3–5] and quantum computers. Probably it is difficult to generate entangled systems with the same dimensions. This task may be difficult if the used devices are imperfect. Moreover, one successes to generate maximum entangled states, but keeping them long-lived entangled is a very difficult task and may cost more [6–9]. These states could be subject to noise channels [10] or dissipative environment [11, 12].
Therefore, it is important to investigate the behavior of entanglement in the presence of a different type of noise. There are several efforts which have been done to investigate the amount of survival entanglement of different systems pass through a different type of noise. For example, Yu and Eberly showed that the dynamics of entanglement between two qubits system interacting independently with classical or quantum noise, displays the phenomena of entanglement decay and entanglement sudden death ESD [13–16]. The dynamics of entanglement and impurity for a bipartite system that passes through Block channels were investigated in [17–19].
One of the most important types of noise is called the intrinsic decoherence noise [20]. For example, M.-L Hu and H.-Li Lian in [21] have investigated the quantum state transfer and the distribution of entanglement in the model of Milburn’s intrinsic decoherence. In [22], R. J.-Amaro et. al have studied the interaction of a two-level atom and two fields, one of them is classical in the dispersive regime by using a model of intrinsic decoherence. The possibility of reducing intrinsic decoherence in a superconducting circuit by quantum error detection is discussed by Zhong, et al. [23]. The effects of inhomogeneous magnetic field on entanglement and teleportation in a two-qubit Heisenberg XXZ chain with intrinsic decoherence have been investigated [24, 25]
Therefore, we have motivated to investigate the behavior of quantum correlation for a system consists of two different dimensional subsystems in the presences of intrinsic decoherence. In this context, we can compare robustness of our suggested model and two-qubit systems to this type of noise. On other word, we need to investigate the effect of the dimensions of the system that pass through this type of noise on the degree of correlations between its subsystems. The rest of this paper is organized as follows. In Section 2, we introduce the suggested model and its analytical solution. Section 3 is devoted to investigate the dynamics of entanglement and quantum correlation by means of negativity [26] and measurement-induced disturbance [27], respectively, where we investigate the effect of different initial state setting, field’s parameters and intrinsic decoherence. Finally, we summarize our results in Section 4.
2 Suggested Model
Let us consider a system consists of spin \(\left (\frac {1}{2}, \frac {3}{2}\right )\), which is described by Heisenberg XXZ model in the presence of a uniform of magnetic field. The Hamiltonian of this system is given by [28]
where J is the coupling constant, k stands for the anisotropy parameter, B i (i = 1,2) is magnetic field applied along the z− direction and \(s_{1}^{\ell },~S_{2}^{\ell }(\ell =x,y,z)\) are the operators for the subsystems of spins \(\frac {1}{2}\) and \(\frac {3}{2}\), respectively. Explicitly, these spin operators can be written as [29]
To investigate the dynamics of a system that doesn’t evolve continuously for a short time steps under unitary operator, one use the model which is introduced by Milburn [20], where the system evolves under the effect of an stochastic sequence of identical unitary transformations. The system is governed by the following differential equation
where γ is the phase decoherence rate, ρ(t) is the density operator of the system and \(\mathcal {H}\) is the Hamiltonian which describes the system. It is clear that from (1), the normal Schrödinger equation can be recovered in the limit γ→0 [22]. For the time t>0, the general solution of this system can be given by
where E m and |ψ m 〉 are the eigenvalues and the corresponding eigenvectors of \(\mathcal {H}\) given in (1) and ρ(0) is the initial density operator of the system. In basis \(\bigl | x,y\bigr \rangle \) \((x=-\frac {1}{2},\frac {1}{2}\) and \(y=-\frac {3}{2},-\frac {1}{ 2},\frac {1}{2},\frac {3}{2})\) , the eigenvalues are given by
where Δ=B 1−B 2. Moreover, the corresponding eigenvectors of these eigenvalues are given by
where
and
To clarify out task, we consider that the system is initially prepared in the state
where
Now, by using (5–10), we can obtain the final state of the system in the basis (8) as a matrix of order 8×8. The non zero elements of this state are given by
with \(\rho _{52}=\rho _{25}^{\ast }\) and \(\rho _{74}=\rho _{47}^{\ast }\).
3 Dynamics Correlations
It is well known that there are some systems could be entangled but have a zero negativity and non-zero values of quantum correlations. This means that there are some quantum correlation can not be predicted by using the negativity as a measure of entanglement [26]. However, by using the measurement-induced disturbance as a measure of quantum correlation, one can quantify the unpredicted quantum correlation [27, 30]. Therefor, we are motivated to investigate the effect of a type of noise called intrinsic decoherence on the negativity and the measurement-induced disturbance
In this section, we investigate the behavior of entanglement in the presences of intrinsic decoherence, by means of negativity \(\mathcal {N}\). This measure states that if {λ μ } represents the eigenvalues of \(\rho _{ab}^{T_{2}}\), then the negativity is given by [26],
where T 2 refers to the partial transposition for the second subsystem. By using this definition for our system, the negativity can be calculated explicitly as,
To quantify the degree of quantum correlation between the two subsystems, Luo in [27] has introduced an acceptable measure called measurement-induced disturbance \(\mathcal {M}_{ID}\). This measure is defined as the difference between the total information of the traveled system I t o t and the classical correlation I c l . It is defined as,
where \(I_{tot}=\mathcal {S}(\rho _{a})+\mathcal {S}(\rho _{b})+\mathcal {S} (\rho _{ab})\) is mutual information of the system and \(\mathcal {S}(.)\) is the von Neumann entropy of the state ρ i ,i = a,b,a b. On the other hand, the classical information I c l is given by the von-Neumann of the state π(ρ), where
Explicitly, one can express the \(\mathcal {M}_{ID}\) as
where
In the following subsection, we investigate numerically the behavior of negativity and measurement-induced disturbance, respectively. This behavior is investigated for different initial state setting, fields polarizations and different values of the intrinsic decoherence.
3.1 Negativity
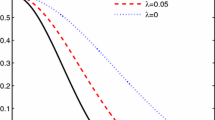
In Fig. 1, we assume that the system is initially prepared in the state |ϕ 1(0)〉, namely, we set ζ 1 = 1 and ζ 2 = 0, for different values of B 1 and B 2. Figure 1a describes the behavior of negativity for small value of the intrinsic decoherence parameter γ. When, B 1 = B 2 = 0, the upper and lower bounds entanglement decrease as the time increases. However, when the fields are switched on different polarization, namely, the parameter Δ increases, the lower and upper bounds of entanglement are increased. This shows that the entanglement increases as the time increases. As Δ increases, the lower and maximum bound of entanglement increase. Figure 1b describes the behavior of negativity for larger value of intrinsic decoherence parameter γ. It is clear that, for small values of time t, the behavior is similar to that which predicted in Fig. 1a. As time t increases, the behavior of negativity becomes stable and there is only tiny fluctuations which disappear for larger values of time t.
The negativity \(\mathcal {N}\) as a function of time t when the system is initially prepared in \(|\protect \phi _{1}(0)\rangle \), for different values of external magnetic field (solid line represents B 1 = B 2 = 0.0, dotted line represents B 1 = −B 2 = 0.1 and dashed line represents B 1 = −B 2 = 0.2), with J = k = 1 and different values of \( \protect \gamma :\) where in (a) \(\protect \gamma =0.05\) and in (b) \(\protect \gamma =0.2\)
From Fig. 1, one can conclude that the degree of entanglement between the subsystems can be increased, if the two fields are switch on different directions. The fluctuations of negativity disappear for larger values of intrinsic decoherence parameter γ and the phenomena of long-lived entanglement appears [32].
In Fig. 2, we investigate the behavior of negativity in the presence of intrinsic decoherence when only one field is switched on, where we set γ = 0.1, B 1 = 0 and different values of B 2. It is clear that, the general behavior of entanglement is similar to that shown in Fig. 1. However, the upper and lower bounds of entanglement decrease as the strength of the second field increases as shown in Fig. 2a. Moreover, the amplitudes of the oscillations decrease as the time increases. Figure 2b shows the behavior of negativity for larger values of intrinsic decoherence parameter, where we set γ = 0.5. In this case, the oscillations collapse for small values of time t and the phenomena of long-lived entanglement appear much earlier than that depicted in Fig. 1b.
The negativity \(\mathcal {N}\) as a function of time t, when the system is initially prepared in the state \(|\protect \phi _{1}(0) \rangle \). For (a) and (b), the solid, dotted and dashed curves are evaluated for B 1 = 0,B 2 = 0.1,0,3,0.5,respectively. For (c) and (d), the solid, dotted and dashed curves are evaluated for B 2 = 0,B 1 = 0.1,0,3,0.5 respectively. For the panels (a) and (c), we consider \(\protect \gamma =0.1\) while for (b) and (d), we set \(\protect \gamma =0.5\)
In Fig. 2c, we assume that only one qubit is subjected to the external field. In this case, the behavior is similar to that depicted in Fig. 2a. However, the upper value of negativity is much larger than that has shown in Fig. 2a. A similar behavior is seen for larger values of intrinsic decoherence parameter γ, where the entanglement is much better than that has displayed in Fig. 2b.
Figure 2 shows that, the degree of entanglement decreases as one of the field’s strength increases. The phenomena of long-lived entanglement appears for larger values of intrinsic decoherence parameter γ. However, the rate decay of entanglement depend on the subsystem which is subjected to the external field.
In Fig. 3, the behavior of negativity is described for different initial state setting, where we consider that the system is initially prepared in the state |ϕ 2(0)〉, namely, we set ζ 1 = 0 and ζ 2 = 1. The behavior of the negativity is similar to that depicted in Fig. 1. For small values of intrinsic decoherence parameter γ = 0.1, the oscillations are shifted as time t increases and the difference between the field’s strength increases i.e. Δ increases. Moreover, for larger values of time t, the upper and lower bound are smaller than their corresponding in Fig. 1a. On the other hand, as one increases the intrinsic decoherence parameter γ, the long-lived entanglement appears but they are smaller than that shown in Fig. 1b.
The negativity \(\mathcal {N}\) as a function of time t when the system is initially prepared in the state \(\bigl |\protect \phi _{2}(0) \bigr \rangle \) and \(\protect \gamma =0.1\) while the others parameters as the same in Fig. 1a
From Figs. 1 and 3, it is clear that the behavior of entanglement depends on the initial state setting. Although that both of the initial states are maximum, but their robustness to the noise is different. These results are similar to that shown for Bell states, where some of them are more robust than the others for some types of noisy.
3.2 Measurement-Induced Disturbance
The amount of quantum correlation between the two subsystems is quantified by means of the measurement-induced disturbance \(\mathcal {M}_{ID}\). The behavior of \(\mathcal {M}_{ID}\) is investigated for different initial states setting. Moreover, the effect of field’s parameters and the intrinsic decoherence noisy on the behavior of quantum correlation are investigated. In Fig. 4, the behavior of \(\mathcal {M}_{ID}\) is described for a system which initially prepared in the state ϕ 1(0)〉. The behavior of \(\mathcal {M}_{ID}\) is similar to that predicated for the negativity as shown in Fig. 1. However, for \(\mathcal {M}_{ID}\) the upper and lower bounds are smaller than that shown for the negativity. Also the amplitudes of the oscillations decrease as the noisy strength increases. Therefore, as time t increases the phenomena of long-lived quantum correlations is displayed clearly.
The behavior of measurement-induced disturbance \(\mathcal {M}_{ID}\) , where the same parameters are considered as Fig. 1
Figure 5 displays the behavior of \(\mathcal {M}_{ID}\), when only one field is switched on, where we fixed all the parameter which are used in Fig. 1. In Fig. 5a, we assume that the only one qubit is subjected to the external field, then the upper bounds of the measurement-induced disturbance decrease faster than the behavior of the negativity which is displayed in Fig. 2a. The behavior of \(\mathcal {M}_{ID}\) when the only one qubit is subjected to the external field is displayed in Fig. 5c. The general behavior is similar to that depicted in Fig. 5a, but the upper bounds are larger. The same result can be seen from Fig. 5b and d, where we consider larger values of intrinsic decoherence parameter γ. This means that the subsystems lose their quantum correlations if any of the subsystems is subject to an external field. However, the system lose more correlation when the larger dimensional subject to the external field. From Fig. 5b and d, it is clear that, for larger values of intrinsic decoherence parameter γ, the phenomena of long-lived quantum correlation between the two subsystems appear as time t increases.
The behavior of measurement-induced disturbance \(\mathcal {M}_{ID}\) , where the same parameters are considered as Fig. 2
The effect of a different initial state setting is described in Fig. 6, where it is assumed that the system is initially prepared in the state |ϕ 2(0)〉. In this case, the behavior of measurement-induced disturbance is completely difference than that shown for negativity (see Fig. 3). It is clear that the upper and lower bounds are much better than that shown for negativity. This means that, the quantum correlation between the two subsystems which are initially prepared in |ϕ 2(0)〉 is more robust than that shown for the system that initially prepared in |ϕ 1(0)〉.
The behavior of measurement-induced disturbance \(\mathcal {M}_{ID}\) where the same parameters are considered as Fig. 3
From the previous discussion, we can conclude that the larger dimensional systems are more robust than the small dimensional systems for this type of noise, where it is shown that for two-qubit systems, the degree of entanglement vanishes as time t increases [34, 35], while for the larger dimensional systems one gets a long-lived entanglement.
4 Conclusion
The dynamics of a composite system consists of two different dimensional subsystem is investigated in the presence of intrinsic decoherence noisy, where the final state of the evolved system is obtained analytically. We discussed two measures: one is called negativity which measures the degree of entanglement between the two subsystems, while the second is called measurement-induced disturbance which measures the total quantum correlation between the two subsystems.
The behavior of these two phenomenon, negativity and measurement-induced disturbance, is discussed for two different initial states setting. It is shown that, the negativity of one state is more robust than measurement-induced disturbance. However, for the second state measurement-induced disturbance is more robust. This shows that, the amount of entanglement and quantum correlation are depend on the initial state setting.
The intrinsic decoherence noisy has an important effect on both two measures, where as one increases the values of intrinsic decoherence’s parameter, the oscillations’s amplitudes decrease with time and consequently the upper bounds decrease and the lower bounds increase for both phenomena. However as time increases, the phenomena of long-lived entanglement and quantum correlations appear.
The behavior of entanglement and measurement-induced disturbance is investigated for different polarization and values of the field’s strengths. Our results show that, when the two fields are switched on different directions, the negativity and measurement-induced disturbance increase as the strengths of the field increase. However, the increasing rate of negativity is larger than that depicted for measurement-induced disturbance, this means that the state contains more quantum information. On the other hand, if only one field is switched on, the upper bounds of both measures decrease. Moreover, if the larger subsystem is subjected to the external field, the decay rate is larger than that shown if the small dimensional subsystem is subjected to the external field.
In conclusion, if we have the ability of controlling the devises, one can generate entangled state with large degree of entanglement and quantum correlation. Although, the presence of intrinsic decoherence decreases the degree of entanglement and quantum correlation, but the survival amount of entanglement and correlations can be used as a long-lived entanglement and quantum correlation. If we can control on the external field, we can improve the degree of correlations between the two subsystems. These results are very important in the context of quantum communication
References
Vedral, V.: Introduction to Quantum Information Science. Oxford University Press, Oxford (2008)
Barnett, S.M.: Quantum Information. Oxford University Press, Oxford (2009)
Metwally, N.: Entangled network and quantum communication. Phys. Lett. A 375, 4268 (2011)
Giraud, O., Georgeot, B., Shepelynasky, D.L.: Quantum computing of delocalization in small-world networks. Phys. Rev. E 72, 036303 (2005)
Metwally, N.: Entanglement routers via a wireless quantum network based on arbitrary two qubit systems. Phys. Scr. 89, 125103 (2014)
Bennett, C.H., Brassard, G., Popescu, S., Schumacher, B., Smolin, J.A., Wootters, W.K.: Purification of noisy entanglement and faithful teleportation via noisy channels. Phys. Rev. Lett. 76, 722 (1996)
Bennett, C.H., DiVincenzo, D.P., Smolin, J.A., Wootters, W.K.: Mixed-state entanglement and quantum error correction. Phys. Rev. A 54, 3824 (1996)
Metwally, N.: More efficient purification protocol. Phys. Rev. A 66, 054302 (2002)
Metwally, N., Obada, A.-S.F.: More efficient Purifying scheme via Controlled-Controlled NOT gate. Phys. Lett. A 352, 45 (2006)
Huang, P., Zhu, J., He, G., Zeng, G.: Study on the security of discrete-variable quantum key distribution over non-Markovian channels. J. Phys. B: At. Mol. Opt. Phys. 45, 135501 (2012)
Hussain, M.I., Ikram, M.: Entanglement engineering of a close bipartite atomic system in a dissipative environment. J. Phys. B: At. Mol. Opt. Phys. 45, 115503 (2012)
Metwally, N.: Information loss in local dissipation environments. Int. J. Theor. Phys. 49, 1571 (2010)
Yu, T., Eberly, J.: Finite-time disentanglement via spontaneous emission. Phys. Rev. Lett. 93, 140404 (2004)
Yu, T., Eberly, J.: Sudden death of entanglement: Classical noise effects. Opt. Commun. 264, 393 (2006)
Metwally, N.: Quantum dense coding and dynamics of information over Bloch channels. J. Phys. A: Math. Theor. 44, 055305 (2011)
Abdel-Aty, M., Yu, T.: Entanglement sudden birth in two three–level trapped ions interacting with a time-dependent laser field. J. Phys. B: At. Mol. Opt. Phys. 41, 235503 (2008)
Ban, M., Kitajima, A., Shibata, F.: Decoherence of entanglement in the Bloch channel. J. Phys. A: Math. Gen. 38, 4235 (2005)
Ban, M., Kitajima, A.-S., Shibata, F.: Decoherence of quantum information in the non-Markovian qubit channel. J. Phys. A: Math. Gen. 38, 7161 (2005)
Metwally, N.: Abrupt decay of entanglement and quantum communication through noise channels. Quantum Inf. Process 9, 429 (2010)
Milburn, G.J.: Intrinsic decoherence in quantum mechanics. Phys. Rev. A 44, 5401 (1991)
Hu, M.L., Li Lian, H.: State transfer in intrinsic decoherence spin channels. Eur. Phys. J. D 55, 711 (2009)
Ju´arez-Amaro, R., Escudero-Jim´enez, J.L., Moya-Cessa, H.: Intrinsic decoherence in the interaction of two fields with a two-level atom. Annalen der Physik 18, 454 (2009)
Zhong, Y.P., Wang, Z. L., Wang, H., John, M., Martinis, M., Cleland, A.N.: Reducing the impact of intrinsic dissipation in a superconducting circuit by quantum error detection. Nat. Commun. 5, 3135 (2014)
Guo, J.-L., H.-S. Song: Effects of inhomogeneous magnetic field on entanglement and teleportation in a two-qubit Heisenberg XXZ chain with intrinsic decoherence. Phys. Scr. 78, 045002 (2008)
Zidan, N.: Quantum teleportation via two-qubit Heisenberg XYZ chain. Can. J. Phys. 92, 406 (2014)
Zyczkowski, K., Horodecki, P., Sanpera, A., Lewenstein, M.: Volume of the set of separable states. Phys. Rev. A 58, 883 (1998)
Luo, S.: Using measurement-induced disturbance to characterize correlations as classical or quantum. Phys. Rev. A 77, 022301 (2008)
Yang, G.-H., Zhou, L.: Entanglement properties of a two-qubit, mixed-spin, Heisenberg chain under a nonuniform magnetic field. Phys. Scr. 78, 025703 (2008)
Nielsen, M.A., Chuang, I.L.: Quantum computation and quantum information. Cambridge University Press, Cambridge (2000)
Song, L., Yang, G.-H.: Entanglement and measurement-induced disturbance about two-qubit Heisenberg XYZ model. Int. J. Theor. Phys. 53, 1985 (2014)
Shadman, Z., Kampermann, H., Macchiavello, C., Bruss, D.: Optimal super dense coding over noisy quantum channels. New J. Phys. 12, 073042 (2010)
Metwally, N.: Single and double changes of entanglement. J. Opt. Soc. Am. B 31, 691 (2014)
Zhang, J., Chen, L., Abdel-Aty, M., Chen, A.: Sudden death and robustness of quantum correlations in the weak- or strong-coupling regime. Eur. Phys. J. D 66, 1 (2012)
Liang, Q.: Quantum correlation in a two-qubit Heisenberg XX model under intrinsic decoherence. Commun. Theor. Phys. 60, 391 (2013)
Xu, X.-B., Liu, J.M., Yu, P.-F.: Entanglement of a two-qubit anisotropic Heisenberg XYZ chain in nonuniform magnetic fields with intrinsic decoherence. Chin. Phys. B 17, 456 (2008)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Zidan, N. Dynamics of Correlations in the Presences of Intrinsic Decoherence. Int J Theor Phys 55, 1274–1284 (2016). https://doi.org/10.1007/s10773-015-2768-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10773-015-2768-y