Abstract
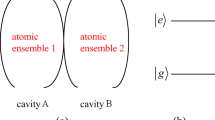
Based on two-photon Jaynes-Cummings Hamiltonian for the n coupled optical cavities each of them containing a single three level atom, the n-qubit and n-photonic state transfer between the corresponding atoms and cavities is investigated. In fact, we consider that the cavities are located at the nodes (vertices) of the complete network (graph) K n at which all of the nodes are connected, so that the cavities are interact with each other (via two photon exchange) completely. Then, quantum state transfer, photon transition between cavities and entanglement generations between n atoms are discussed. More clearly, by employing the consistency of number of photons and atomic excitations (the symmetry of Hamiltonian), the hamiltonian of the system is reduced from 3n dimensional space into 2n dimensional one. Moreover, by introducing suitable basis for the atom-cavity state space based on Fourier transform, the reduced Hamiltonian is block-diagonalized, with 2 dimensional blocks. Then, the initial state of the system is evolved under the corresponding Hamiltonian and the suitable times T at which the initially unentangled atoms, become maximally entangled, are determined in terms of the hopping strength ξ between cavities.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Bouwmeester, D. et al.: The Physics of Quantum Information. Springer, Berlin Heidelberg New York (2000)
Christandl, M., Datta, N., Ekert, A., Landahl, A.J.: Phys. Rev. Lett. 92, 187902 (2004)
Christandl, M., Datta, N., Dorlas, T.C., Ekert, A., Kay, A., Landahl, A.J.: Phys. Rev. A. 71, 032312 (2005)
Facer, C., Twamley, J., Cresser, J.: Phys. Rev. A 77, 012334 (2008)
Burgarth, D., Bose, S.: Phys. Rev. A 71, 052315 (2005)
Burgarth, D., Bose, S.: New J. Phys. 7, 135 (2005)
Yung, M.H., Bose, S.: Phys. Rev. A 71, 032310 (2005)
Yung, M.H.: Phys. Rev. A 74, 030303 (2006)
Jafarizadeh, M.A., Sufiani, R.: Phys. Rev. A 77, 022315 (2008)
Jafarizadeh, M.A., et al.: J. Phys. A: Math. Theor. 41, 475302 (2008)
Jafarizadeh, M.A., et al.: J. Stat. Mech., 05014 (2011)
Turchette, Q.A., Hood, C.J., Lange, W., Mabuchi, H., Kimble, H.J.: Phys. Rev. Lett. 75, 4710 (1995)
Brune, M., et al.: Phys. Rev. Lett. 77, 4887 (1996)
Mattle, K., Weinfurter, H., Kwiat, P.G., Zeilinger, A.: Phys. Rev. Lett. 76, 4656 (1996)
Biswas, A., Agarwal, G.S.: Phys. Rev. A 70, 022323 (2004)
Cirac, J.I., Zoller, P., Kimble, H.J., Mabuchi, H.: Phys. Rev. Lett. 78, 3221 (1997)
Alexanian, M., et al.: J. Mod. Opt. 45, 2519 (1998)
Alexanian, M.: Phys. Rev. A 83, 023814 (2011)
Alexanian, M.: arXiv:quant-ph:12034173 (2012)
Dong, Y.-L., et al.: Phys. Rev. A 85, 023833 (2012)
Hardal, A.Ü.C., Mstecaplioglu, Ö.E.: J. Opt. Soc. Am. B 29, 1822–1828 (2012)
Sufiani, R.: Quantum state transfer in atom-cavity systems with uncolored Cayley interacting networks. Int. J. Theor. Phys. (2014). doi:10.1007/s10773-014-2213-7
Puri, R.R.: Mathematical Methods of Quantum Optics. Springer, Berlin Heidelberg New York (2001)
Scully, M.O., Zubairy, M.S.: Quantum Optics. Cambridge University Press, Cambridge, UK (1997)
Hillery, M.: Acta physica slovaca. Rev. Tutor. 59, 1 (2009)
DellAnno, F., De Siena, S., Illuminati, F.: Phys. Rep. 428, 53 (2006)
Buzek, V., Hladky, B.: J. Mod. Opt. 40, 1309 (1998)
Peres, A.: Phys. Rev. Lett. 77, 1413–1415 (1996)
Horodecki, M. et al.: Phys. Lett. A 223, 1–8 (1996)
Wootters, W.K.: Phys. Rev. Lett. 80, 2245–2248 (1998)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Sufiani, R., Darkhosh, A. Atomic and Photonic Entanglement Generation in n Coupled Atom-Cavity Systems. Int J Theor Phys 54, 2299–2311 (2015). https://doi.org/10.1007/s10773-014-2452-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10773-014-2452-7