Abstract
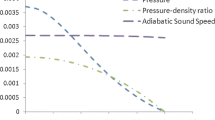
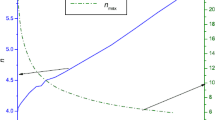
We present a spherically symmetric solution of the general relativistic field equations in isotropic coordinates for perfect fluid, compatible with a super dense star modeling. The solution is well behaved for all the values of u lying in the range 0<u≤0.12. Further, we have constructed a super-dense star model with all degree of suitability and by assuming the surface density ρ b =2×1014 g/cm3. Corresponding to u=0.12, the resulting well behaved model has maximum mass M=0.912M Θ with radius R b ≈11.27 km and Moment of inertia 0.97×1045 gm cm2. The good matching of our results for Vela pulsars show the stoutness of our model.


Similar content being viewed by others
References
Delgaty, M.S.R., Lake, K.: Comput. Phys. Commun. 115, 395 (1998)
Tolman, R.C.: Phys. Rev. 55, 364 (1939)
Adler, R.J.: J. Math. Phys. 15, 727 (1974)
Heintzmann, H.: Z. Phys. 228, 489 (1969)
Finch, N.R., Skea, J.E.F.: Class. Quantum Gravity 6, 467 (1989)
Patwardhan, G.K., Vaidya, P.C.: J. Univ. Bombay 12, 23 (1943). Part III
Mehra, A.L.: J. Aust. Math. Soc. 6, 153 (1966)
Kuchowicz, B.: Acta Phys. Pol. 34, 131 (1968)
Matese, J.J., Whitman, P.G.: Phys. Rev. D 22, 1270 (1980)
Durgapal, M.C.: J. Phys. A, Math. Gen. 15, 2637 (1982)
Nariai, S.: Sci. Rep. Tohoku Univ., Ser. 1 34, 160 (1950)
Goldman, S.P.: Astrophys. J. 226, 1079 (1978)
Pant, N.: Astrophys. Space Sci. 331, 633 (2011)
Maurya, S.K., Gupta, K.: Astrophys. Space Sci. (2011). doi:10.1007s10509-011-0705-y
Pant, N., et al.: Astrophys. Space Sci. 330, 353 (2010)
Pant, N., et al.: Astrophys. Space Sci. 340, 407 (2012)
Ivanov, B.V.: Gen. Relativ. Gravit. 44, 1835 (2012)
Kramer, D.: J. Math. Phys. 33, 1458 (1992)
Banerjee, A., Chatterjee, S., Dadhich, N.: Mod. Phys. Lett. A 35, 2335 (2002)
Tewari, B.C.: Astrophys. Space Sci. 342, 73 (2012)
Pant, N., Negi, P.S.: Astrophys. Space Sci. 338, 163 (2012)
Canuto, V., Lodenquai, J.: Phys. Rev. C 12, 2033 (1975)
Pant, N., et al.: Appl. Math. Comput. 218, 8260 (2012). doi:10.1016/j.amc.2012.01.044
Hajj Boutros, J.: J. Math. Phys. 27, 1363 (1986)
Bejger, M., Haensel, P.: Astron. Astrophys. 396, 917 (2002)
Acknowledgement
One of us (Neeraj Pant) is grateful to Air Marshal K.S. Gill AVSM YSM VM, the Commandant NDA Khadakwasla Pune for his motivation and encouragement. We are grateful to the anonymous referees for making constructive and relevant suggestions.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Pant, N., Fuloria, P. & Pradhan, N. An Exact Solution of Perfect Fluid in Isotropic Coordinates, Compatible with Relativistic Modeling of Star. Int J Theor Phys 53, 993–1002 (2014). https://doi.org/10.1007/s10773-013-1892-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10773-013-1892-9