Skip to main content
SpringerLink
Log in

Quantum Signature Scheme with Weak Arbitrator

  • Published:
International Journal of Theoretical Physics Aims and scope Submit manuscript

Abstract

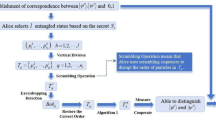
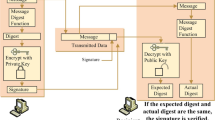
In this paper, we propose one quantum signature scheme with a weak arbitrator to sign classical messages. This scheme can preserve the merits in the original arbitrated scheme with some entanglement resources, and provide a higher efficiency in transmission and reduction the complexity of implementation. The arbitrator is costless and only involved in the disagreement case.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1

Similar content being viewed by others

References

  1. Shor, P.W.: SIAM J. Comput. 26(5), 1484–1509 (1997)

    Article  MathSciNet  MATH  Google Scholar 

  2. Dumais, P., Mayers, D., Salvail, L.: Advances in Cryptology-Eurocrypt 2000, LNSC vol. 1807, pp. 300–315. Springer, Berlin (2000),

    Book  Google Scholar 

  3. Crépeau, C., Légaré, F., Salvail, L.: In: Proc. Euro Advances in Cryptology (2001)

  4. Kashefi, E., Kerenidis, I.: Theor. Comput. Sci. 378(1), 101–116 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  5. Kawachi, A., Kobayashi, H., Koshiba, T., Putra, R.H.: Theor. Comput. Sci. 345, 370–385 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  6. Zeng, G.H., Keitel, C.H.: Phys. Rev. A 65, 042312 (2002)

    Article  MathSciNet  ADS  Google Scholar 

  7. Lee, H., Hong, C., Kim, H., Lim, J., Yang, H.J.: Phys. Lett. A 321, 295 (2004)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  8. Wen, X.J., Liu, Y., Sun, Y.: Z. Naturforsch. A, J. Phys. Sci. 62a, 147 (2007)

    Google Scholar 

  9. Zeng, G.H., Lee, M., Guo, Y., He, G.Q.: Int. J. Quantum Inf. 5, 553 (2007)

    Article  MATH  Google Scholar 

  10. Gottesman, D., Chuang, I.L.: e-print arXiv:quant-ph/0105032

  11. Li, Q., Chan, W.H., Long, D.Y.: Phys. Rev. A 79, 054307 (2009)

    Article  MathSciNet  ADS  Google Scholar 

  12. Greenberger, D.M., Horne, M.A., Zeilinger, A.: In: Bell’s Theorem, Quantum Theory, and Conceptions of the Universe, pp. 73–76. Kluwer Academics, Dordrecht (1989)

    Google Scholar 

  13. Goldreich, O.: Foundations of Cryptography. Cambridge University Press, Cambridge (2001)

    Book  MATH  Google Scholar 

  14. Aharonov, D., Ta-shma, A.: arXiv:quant-ph/0301023

  15. Buhrman, H., Cleve, R., Watrous, J., de Wolf, R.: Phys. Rev. Lett. 87, 167902 (2001)

    Article  ADS  Google Scholar 

  16. Braunstein, S.L., Caves, C.M.: Phys. Rev. Lett. 72, 3439–3443 (1994)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  17. Walgate, J., Short, A.J., Hardy, L., Vedral, V.: Phys. Rev. Lett. 85, 4972–4975 (2000)

    Article  ADS  Google Scholar 

  18. Xiang, G.Y., Li, J., Guo, G.C.: Phys. Rev. A 71, 044304 (2005)

    Article  ADS  Google Scholar 

  19. Nikolopoulos, G.M.: Phys. Rev. A 77, 032348 (2008)

    Article  MathSciNet  ADS  Google Scholar 

Download references

Acknowledgements

This work is supported by the National Natural Science Foundation of China (Nos. 61003287, 61170272); the Specialized Research Fund for the Doctoral Program of Higher Education (No. 20100005120002), and the Fundamental Research Funds for the Central Universities (No. SWJTU11BR174).

Author information

Authors and Affiliations

  1. Information Security Center, Beijing University of Posts and Telecommunications, Beijing, 100876, China

    Ming-Xing Luo, Xiu-Bo Chen & Yi-Xian Yang

  2. State Key Laboratory of Information Security, Graduate University of Chinese Academy of Sciences, Beijing, 100049, China

    Ming-Xing Luo, Xiu-Bo Chen & Yi-Xian Yang

  3. Information Security and National Computing Grid Laboratory, School of Information Science and Technology, Southwest Jiaotong University, Chengdu, 610031, China

    Ming-Xing Luo, Xiu-Bo Chen & Yi-Xian Yang

  4. Institute of Computer Science, Sichuan University of Science & Engineering, Zigong, 643000, China

    Deng Yun

Authors
  1. Ming-Xing Luo
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Xiu-Bo Chen
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Deng Yun
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Yi-Xian Yang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Ming-Xing Luo.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Luo, MX., Chen, XB., Yun, D. et al. Quantum Signature Scheme with Weak Arbitrator. Int J Theor Phys 51, 2135–2142 (2012). https://doi.org/10.1007/s10773-012-1093-y

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10773-012-1093-y

Keywords

Search

Navigation