Skip to main content
SpringerLink
Log in

Phantom Accretion onto the Schwarzschild Anti de-Sitter Black Hole

  • Published:
International Journal of Theoretical Physics Aims and scope Submit manuscript

Abstract

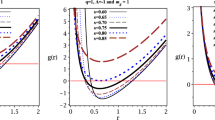
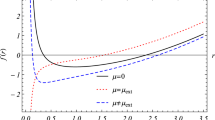
In this paper we study phantom energy accretion onto the Schwarzschild anti de-Sitter black hole. We obtain critical point where the speed of flow is equal speed of sound. We find that the critical point is near the black hole horizon.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Bondi, H.: Mon. Not. R. Astron. Soc. 112, 195 (1952)

    MathSciNet  ADS  Google Scholar 

  2. Michel, F.C.: Astrophys. Space Sci. 15, 153 (1972)

    Article  ADS  Google Scholar 

  3. Babichev, E., Dokuchaev, V., Eroshenko, Y.: Phys. Rev. Lett. 93, 021102 (2004)

    Article  ADS  Google Scholar 

  4. Jamil, M., Rashid, M., Qadir, A.: Eur. Phys. J. C 58, 325 (2008)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  5. Babichev, E., Chernov, S., Dokuchaev, V., Eroshenko, Y.: J. Exp. Theor. Phys. 112784 (2011)

  6. Jiménez Madrid, J.A., González-Diaz, P.F.: Gravit. Cosmol. 14(3), 213–225 (2008)

    Article  MathSciNet  ADS  Google Scholar 

  7. Sharif, M., Abbas, G.: Mod. Phys. Lett. A 26, 1731 (2011)

    Article  ADS  Google Scholar 

  8. Sharif, M., Abbas, G.: Phantom accretion onto the Schwarzschild de-Sitter black hole. [arXiv:1109.1043 [gr-qc]] (2011)

  9. Sung-Won, K.: J. Korean Phys. Soc. 24, 118 (1991)

    Google Scholar 

  10. Chang, J.-F., Shen, Y.-G.: Massive quasinormal modes of a Schwarzschild-de Sitter black hole with a global monopole. Int. J. Theor. Phys. 45(12), 2357 (2006)

    Article  MathSciNet  Google Scholar 

  11. Hossain Ali, M., Atiqur Rahman, M.: Transverse wave propagation in relativistic two-fluid plasmas around Schwarzschild-de Sitter black hole. Int. J. Theor. Phys. 48, 1717 (2009)

    Article  MATH  Google Scholar 

  12. Chang, J.-F., Huang, J., Shen, Y.-G.: Quasi-resonant modes of massive scalar fields in Schwarzschild–de Sitter space-time. Int. J. Theor. Phys. 46, 2617 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  13. Sen, A.: Developments in superstring theory. hep-th/9810356 v 2 (1998)

  14. Maldacena, J.: Adv. Theor. Math. Phys. 2, 231 (1998)

    MathSciNet  ADS  MATH  Google Scholar 

  15. Witten, E.: Adv. Theor. Math. Phys. 2, 253 (1998)

    MathSciNet  MATH  Google Scholar 

  16. Zeng, X.-X., Lin, K., Yang, S.-Z.: Hawking radiation from the higher-dimensional Schwarzschild de Sitter and anti-de Sitter black holes via covariant anomaly. Int. J. Theor. Phys. 47, 2533 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  17. Han, Y.-W., Yang, S.-Z.: Quantum corrections to the radiation of Schwarzschild-anti-de Sitter black hole with topological defect. Commun. Theor. Phys. 47, 1145 (2007)

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

It is pleasure to thank Islamic Azad University, Ayatollah Amoli Branch for supporting this manuscript.

Author information

Authors and Affiliations

  1. Department of Physics, Ayatollah Amoli Branch, Islamic Azad University, P.O. Box 678, Amol, Iran

    A. R. Amani & H. Farahani

Authors
  1. A. R. Amani
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. H. Farahani
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to H. Farahani.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Amani, A.R., Farahani, H. Phantom Accretion onto the Schwarzschild Anti de-Sitter Black Hole. Int J Theor Phys 51, 1498–1502 (2012). https://doi.org/10.1007/s10773-011-1025-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10773-011-1025-2

Keywords

Search

Navigation