Might Dark Matter and Energy be Intrinsic Properties of Space?

Abstract

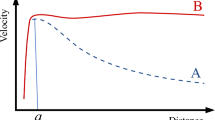
It is shown that if a volume element V, of space is assumed to have intrinsic energy E, then basic principles of mechanics, thermodynamics and special relativity lead to the equation of state: E=pV, where p is the pressure. When this equation of state is incorporated in the Einstein equations it leads to the prediction that the orbital speed of matter circling a visible galaxy embedded in a spherical galactic halo should be relativistic, in disagreement with observations. However, it also leads directly to the interesting notion that the inertial mass of such a medium can be understood as a resistance to being compressed via Lorentz contraction. It is then shown that the mathematical structure of thermodynamics suggests another plausible definition of pressure if we allow for the possibility that the intrinsic energy of spacetime may not be described by the same work-energy relationship as ordinary matter. This additional possibility leads to the equation of state: E=−pV. While both of these equations of state describe forms of energy that are quite unlike ordinary energy, neither alone is able to account for observed rotational velocity curves of matter orbiting visible galaxies. Therefore, the possibility that space has two distinct components of energy is investigated. This results in a plausible, two-component equation of state in which the former equation of state is tentatively identified as the “dark matter” (DM) component, the latter as the “dark energy” (DE) component. The effective equation of state of space, accounting for the presence of both components, may then be written in the form: p=w ε, where ε is the total energy density, p the total pressure, and w represents the fractional excess of DM over DE (and therefore satisfies: −1≤w≤+1). Given the wide range of possible spacetime properties implied by this equation it appears to be a viable candidate for explaining observations presently attributed to the presence of both DM and DE. Specifically, the static, spherically symmetric solution of Einstein’s field equations, neglecting effects of ordinary matter, predicts the inverse r ² distribution of intrinsic space energy required to explain observed constant rotational velocity curves for matter in circular orbits around visible galaxies embedded within spherically symmetric galactic halos. The proposed equation of state is also capable of describing regions of space undergoing accelerated expansion as regions where DE is dominant (i.e., w<−1/3).