Abstract
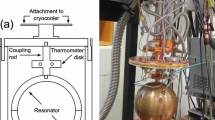
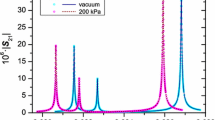
Single-pressure refractive index gas thermometry (SPRIGT) is a new type of primary thermometry, which needs an extremely stable working pressure (stability < 4 ppm). In practice, the pressure control system at room temperature is located above the cold resonator at 5 K to 25 K, and a long pressure tube is used to connect them, which entails a hydrostatic pressure correction (HPC). To this end, a three-dimensional (3D) Computational Fluid Dynamics (CFD) simulation model of the pressure tube has been developed and compared with experimental results. First, to verify the simulation results, the helium-4 gas pressure in the center of the resonator was measured using a determination of the refractive index by microwave resonance coupled with the knowledge of the temperature. Results of simulation and experiment showed good agreement. Thereafter, based on this CFD simulation, the non-linear temperature distribution in the vertical pressure tube and the uncertainty caused by this non-linear phenomenon were calculated. After this, the validity of the isothermal assumption to simplify the calculation of the HPC was verified. Finally, the effect of heating on the pressure was studied and its impact found to be negligible. To the best of our knowledge, this is the first time experimental and simulation results have been compared for the HPC. The results are expected to be more generally applicable to the accurate determination of pressure in cryostats.










Similar content being viewed by others
References
B. Gao, L. Pitre, E.C. Luo et al., Feasibility of primary thermometry using refractive index measurements at a single pressure. Measurement 103, 258–262 (2017)
P.M.C. Rourke, NRC microwave refractive index gas thermometry implementation between 24.5 K and 84 K. Int. J. Thermophys. 38, 1–27 (2017)
L. Pitre, M.R. Moldover, W.L. Tew, Acoustic thermometry: new results from 273 K to 77 K and progress towards 4 K. Metrologia 43, 142–162 (2006)
B. Gao, C.Z. Pan, L. Pitre et al., Chinese SPRIGT realizes high temperature stability in the range of 5–25 K. Sci. Bull. 63, 733–734 (2018)
B. Gao, C.Z. Pan, Y.Y. Chen et al., Realization of an ultra-high precision temperature control in a cryogen-free cryostat. Rev. Sci. Instrum. 89, 104901 (2018)
H.Y. Zhang, W.J. Liu, B. Gao et al., A high-stability quasi-spherical resonator in SPRIGT for microwave frequency measurement at low temperatures. Sci. Bull. 64, 286–288 (2019)
D.X. Han, B. Gao, H. Chen et al., Ultra-stable pressure is realized for Chinese single pressure refractive index gas thermometry in the range 30–90 kPa. Sci. Bull. 63, 1601–1603 (2018)
C. Meyer, M. Reilly, Realization of the ITS-90 at the NIST in the range 0.65 K to 5.0 K using the 3He and 4He vapour-pressure thermometry. Metrologia 33, 383–389 (1996)
K.D. Hill, Realizing the ITS-90 below 4.2 K at the National Research Council of Canada. Metrologia 39, 41–49 (2002)
A. Peruzzi, R. Bosma, M.J. de Groot et al., 4He interpolating constant-volume gas thermometry in the range 3.0 K to 24.5561 K. Metrologia 47, 325–333 (2010)
D.N. Astrov, L.B. Beliansky, Y.A. Dedikov, S.P. Polunin, A.A. Zakharov, Precision gas thermometry between 2.5 K and 308 K. Metrologia 26, 151–166 (1989)
F. Sparasci, L. Pitre, D. Truong, L. Risegari, Realization of a 3He–4He vapor-pressure thermometer for temperatures between 0.65 K and 5 K at LNE-CNAM. Int. J. Thermophys. 32, 139–152 (2011)
F. Pavese, G.M.M. Beciet, Modern gas-based temperature and pressure measurements (Springer Science & Business Media, Berlin, 2012)
P.P.M. Steur and F. Pavese, Recent progress with the IMGC 3He gas thermometer, in 19th International Congress of Refrigeration, The Hague, Netherlands, August 20-25 1995, poster B53 in Physica B + C, Proceedings vol. IIIb, 1241–1246 (1995)
Y.Y. Chen, H.Z. Zhang, Y.N. Song et al., Thermal response characteristics of a SPRIGT primary thermometry system. Cryogenics 97, 1–6 (2019)
C. Pan, T. Zhang, J. Wang, Y. Zhou, CFD study of heat transfer and pressure drop for oscillating flow in helical rectangular channel heat exchanger. Int. J. Thermal Sci. 129, 106–114 (2018)
Y.P. Banjare, R.K. Sahoo, S.K. Sarangi, CFD simulation of a Gifford–McMahon type pulse tube refrigerator. Int. J. Thermal Sci. 48, 2280–2287 (2009)
L. Wang, T. Yan, J. Wang et al., CFD investigation on thermodynamic characteristics in liquid hydrogen tank during successive varied-gravity conditions. Cryogenics 103, 102973 (2019)
ANSYS Academic (Version: 19.2) https://www.ansys.com/en-in/academic/free-student-products
Eric W. Lemmon, Marcia L. Huber and Mark O. McLinden. NIST reference fluid thermodynamic and transport properties—REFPROP Version 9.1 (2013)
E.D. Marquardt, J.P. Le, R. Radebaugh, Cryogenic material properties database//Cryocoolers 11 (Springer, Boston, 2002), pp. 681–687
F. Sharipov, Data on the velocity slip and temperature jump on a gas–solid interface. J. Phys. Chem. Ref. Data 40, 023101 (2011)
J. Ferziger, M. Peric, Computational method for fluid dynamics (Springer, Berlin, 2002)
G.H. Schiroky, F. Rosenberger, Free convection of gases in a horizontal cylinder with differentially heated end walls. Int. J. Heat Mass Tran. 27, 587–598 (1984)
J.W. Schmidt, R.M. Gavioso, E.F. May, M.R. Moldover, Polarizability of helium and gas metrology. Phys. Rev. Lett. 98, 254504 (2007)
P.M.C. Rourke, C. Gaiser, B. Gao et al., Refractive-index gas thermometry. Metrologia 56, 032001 (2019)
N.J. Simon, E.S. Drexler, R.P. Reed, Properties of Copper and Copper Alloys at Cryogenic Temperatures (NIST Monograph 177 (National Institute of Standards and Technology, Boulder, 1992)
NIST Cryogenic Materials Properties Database, OFHC Copper (UNS C10100/C10200) entry, revised 02 Mar 2010
C. Gaiser, B. Fellmuth, Polarizability of helium, neon, and argon: new perspectives for gas metrology. Phys. Rev. Lett. 120, 123203 (2018)
L.W. Bruch and F. Weinhold, Nuclear motion and Breit–Pauli corrections to the diamagnetism of atomic helium. J. Chem. Phys. 117(7) 3243–3247 (2002) and Erratum J. Chem. Phys. 119, 638 (2003)
M.R. Moldover, R.M. Gavioso, J.B. Mehl et al., Acoustic gas thermometry. Metrologia 51, R1–R19 (2014)
K.R.S. Shaul, A.J. Schultz, D.A. Kofke, Path-integral Mayer-sampling calculations of the quantum Boltzmann contribution to virial coefficients of helium-4. J. Chem. Phys. 137, 184101 (2012)
K.H. Berry, NPL-75: a low temperature gas thermometry scale from 2.6 K to 27.1 K. Metrologia 15, 89–115 (1979)
J. Fischer, M. De Podesta, K.D. Hill et al., Present estimates of the differences between thermodynamic temperatures and the ITS-90. Int. J. Thermophys. 32, 12–25 (2011)
B. Fellmuth, J. Engert, T. Shimazaki and F. Sparasci. Guide to the realization of the ITS-90, Chapter 3: Vapour Pressure Scales and Pressure Measurements (Sèvres: Bureau International des Poids et Mesures) p. 22. https://bipm.org/en/committees/cc/cct/guide-its90.html. Accessed 1 Jan 2018
J. Engert, and B. Fellmuth.3He Vapour‐pressure measurements at PTB//AIP, in Proc. temperature: its measurement and control in science and industry, Vol. 7, Ed. D.C. Ripple et al. (AIP, Melville, New York) 684(1) 113–118 (2003)
Acknowledgments
This work was supported by the National Key R&D Program of China (Grant No. 2016YFE0204200), the National Natural Science Foundation of China (Grant No. 51627809), the International Partnership Program of the Chinese Academy of Sciences (Grant No. 1A1111KYSB20160017) and the European Metrology Research Programme (EMRP) Joint Research Project 18SIB02 “Real-K”. Changzhao Pan was supported by funding provided by a Horizon 2020 Marie Skłodowska Curie Individual Fellowship 2018 (No. 834024). The authors thank Duowu Su from NIM for the measurement of g at TIPC (Technical Institute of Physics and Chemistry, Chinese Academy of Sciences) in Langfang.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Appendix
Appendix
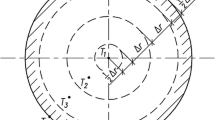
1.1 Uncertainty Budget for the Determination of the HPC at the Temperature of the Neon Triple Point
References to the literature are given for the electromagnetic and density virial coefficients.
Working pressure | 30 kPa | 60 kPa | 90 kPa |
|---|---|---|---|
Pressure in the resonator/Pa | |||
Uncertainty component, type B | |||
T of neon triple point | 0.527 | 0.998 | 1.530 |
\(A_{\varepsilon }\) [29] | 0.003 | 0.007 | 0.01 |
\(B_{\varepsilon }\) [30] | 0.048 | 0.187 | 0.422 |
\(C_{\varepsilon }\) [25] | 0.001 | 0.004 | 0.014 |
\(A_{\mu }\) [31] | 0.002 | 0.001 | 0.001 |
B [32] | 0.001 | 0.005 | 0.012 |
C [32] | – | – | – |
D [32] | – | – | – |
0.051 | 0.105 | 0.157 | |
Uncertainty component, type A | |||
\(f + g_{0} /f + g_{p}\) | 0.035 | 0.032 | 0.104 |
T stability | 0.012 | 0.025 | 0.037 |
Pressure at room temperature/Pa | |||
Uncertainty components, type B | |||
p calibration | 0.306 | 0.606 | 0.903 |
Uncertainty components, type A | |||
p stability | 0.003 | 0.003 | 0.004 |
Combined standard uncertainty/Pa | |||
HPC | 0.617 | 1.188 | 1.836 |
Rights and permissions
About this article
Cite this article
Pan, C., Chen, H., Han, D. et al. Numerical and Experimental Study of the Hydrostatic Pressure Correction in Gas Thermometry: A Case in the SPRIGT. Int J Thermophys 41, 108 (2020). https://doi.org/10.1007/s10765-020-02686-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10765-020-02686-9