Abstract
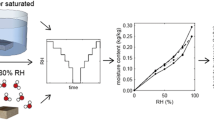
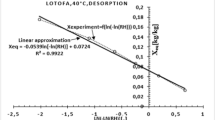
Sorption isotherms relate the equilibrium condition between the moisture content of a solid material and the relative humidity of ambient where such material is placed. Isotherms are useful in many fields where the water vapor of ambient affects the properties of materials. In particular, the information given by the sorption isotherms is useful in the moisture conditioning of solid materials, which are used for the calibration of moisture meters for grains, cereals and wood, among others. There are many isotherm models (almost one for each material). However, most of them do not estimate the uncertainty or, in some cases, the estimation is incomplete. On the other hand, the most known method for uncertainty evaluation is given by the Guide to the Expression of Uncertainty in Measurement (GUM). However, this guide has some restrictions to be satisfactorily used; for example, the model of measurand must be linear and have a known probability distribution function for the model inputs and similar uncertainty values. So often, the sorption isotherm models used for grains are highly nonlinear. Therefore, the GUM could not provide reliable results. To overcome this, an alternative method is the use of Monte Carlo simulation method, which is suggested for nonlinear models in the GUM supplement. In this paper, the uncertainty estimation was done with the GUM and Monte Carlo methods applied to some sorption isotherms, which are used for grains and cereals. The results with both methods showed some discrepancies, which are due mainly to the nonlinearity of models.




Similar content being viewed by others
References
S.M. Henderson, A basic concept of equilibrium moisture. Agric. Eng. 33, 29–32 (1952)
S. Brunauer, The Adsorption of Gases and Vapors, Volume I-Physical Adsorption (Oxford University Press, Oxford, 1943)
R.D. Andrade, R. Lemus, C.E. Pérez, Models of sorption isotherms for food: uses and limitations. Vitae Colomb. 18, 325–334 (2011)
Joint Committee for Guides in Metrology, Evaluation of Measurement Data-Guide to the Expression of Uncertainty of Measurement (GUM), JCGM 100 (2008)
E.O. Timmermann, J. Chirife, H.A. Iglesias, Water sorption isotherms of foods and foodstuffs: BET or GAB parameters? J. Food Eng. 48, 19–31 (2001)
C.C. Chen, Modification of Oswin EMC/ERH equation. J. Agric. Res. China 39, 367–376 (1990)
ASAE D245.5 JAN01, Moisture Relationships of Plant-Based Agricultural Products (2001)
T.V. Anderson, Efficient, Accurate, and Non-Gaussian Statistical Error propagation Through Nonlinear, Closed-Form, Analytical System Models. Master of Science Thesis, Brigham Young University (2011)
Joint Committee for Guides in Metrology, Evaluation of Measurement Data- Supplement 1 to the “Guide to the expression of uncertainty of Measurement”-Propagation of Distributions using Monte Carlo Method, JCGM 101 (2008)
M.G. Cox, M.P. Dainton, P.M. Harris, 2001 Software Support for Metrology Best Practice Guide No. 6: Uncertainty and Statistical Modeling NPL (2001)
I. Farrance, R. Frenkel, Uncertainty in measurement: a review of monte carlo simulation using microsoft excel for the calculation of uncertainties through functional relationships, including uncertainties in empirically derived constants. Clin. Biochem. Rev. 35, 37 (2014)
A. Yegnan, D.G. Williamson, A.J. Graettinger, Uncertainty analysis in air dispersion modelling. Environ. Modell. Softw. 17, 639–649 (2002)
Author information
Authors and Affiliations
Corresponding author
Additional information
Selected Papers of the 13th International Symposium on Temperature, Humidity, Moisture and Thermal Measurements in Industry and Science.
Rights and permissions
About this article
Cite this article
Martines-López, E., Lira-Cortés, L. Uncertainty Estimation of Some Sorption Isotherms Used for the Moisture Conditioning of Grains. Int J Thermophys 39, 138 (2018). https://doi.org/10.1007/s10765-018-2457-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10765-018-2457-1