A Thermo-mechanical Shock Problem for Generalized Theory of Thermoviscoelasticity

Abstract

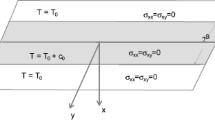
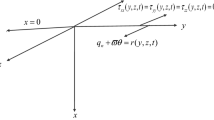
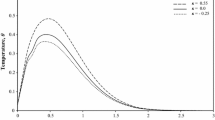
A one-dimensional problem for a viscoelastic half space is considered in the context of the generalized theory of thermoviscoelasticity with one relaxation time. The bounding plane is acted upon by a combination of thermal and mechanical shock acting for short times. The Laplace transform technique is used to solve the problem. The solution in the transformed domain is obtained by a direct approach. The inverse transforms are obtained in an approximate analytical manner using asymptotic expansions valid for small values of time. The temperature, displacement, and stress are computed and represented graphically.

Appendix

 

$$\begin{aligned} v_0&= \sqrt{g_0^2 -4\tau _0 \left( {1-B_1 } \right)} \\ v_1&= 2g_0 g_1 -4\left( {1-B_1 -\tau _0 \beta B} \right)_1 \\ v_2&= g_1^2 +2g_0 g_2 +4B_1 \beta \left( {1+\beta \tau _0 } \right)\\ v_3&= 2\left( {g_0 g_3 +g_1 g_2 } \right)+4B_1 \beta ^{2}\left({1+\beta \tau _0 } \right) \\ v_4&= g_2^2 +2\left( {g_0 g_4 +g_1 g_3 } \right)+4B_1 \beta ^{3}\left( {1+\beta \tau _0 } \right) \\ g_0&= 1+\tau _0 \left( {1-B_1 -\varepsilon \left( {B_2 -B_3 } \right)^{2}} \right) \\ g_1&= 1-B_1 -\varepsilon \left( {B_2 -B_3 } \right)^{2}+\tau _0 \varepsilon B_1 2 \\ g_2&= -\left( {B_1 \beta +\tau _0 \varepsilon B_3^2 \beta ^{2}+\tau _0 B_1 \beta ^{2}} \right) \\ g_3&= -\left( {B_1 \beta ^{2}+2\tau _0 \varepsilon B_3^2 \beta ^{3}+\tau _0 B_1 \beta ^{3}+\varepsilon B_3^2 \beta ^{2}} \right) \\ g_4&= -\left( {B_1 \beta ^{3}+3\tau _0 \varepsilon B_3^2 \beta ^{4}+\tau _0 B_1 \beta ^{4}+2\varepsilon B_3^2 \beta ^{3}} \right)\\ B_1&= \alpha _1 A_1 +2\alpha _2 A_2 \\ B_2&= 3\alpha _1 +2\alpha _2 \\ B_3&= 3\alpha _1 A_1 +2\alpha _2 A_2 \\ B_4&= B_2 -B_3\\ n_{10}&= g_0 +v_0 \\ n_{11}&= \frac{2g_1 v_0 +v_1 }{2v_0 } \\ n_{12}&= \frac{8g_2 v_0^3 +4v_2 v_0^2 -v_1^2 }{8v_0^3 } \\ n_{13}&= \frac{16g_3 v_0^5 -4v_2 v_1 v_0^2 +v_1^3 +8v_3 v_0^4 }{16v_0^5 } \\ n_{14}&= \frac{128g_3 v_0^7 +64v_4 v_0^6 -32v_3 v_1 v_0^4 -16v_0^4 v_2^2 +24v_1^2 v_2 v_0^2 -5v_1^4 }{128v_0^7 } \\ n_{20}&= g_0 -v_0 \\ n_{21}&= \frac{2g_1 v_0 -v_1 }{2v_0 } \\ n_{22}&= \frac{8g_2 v_0^3 -4v_2 v_0^2 +v_1^2 }{8v_0^3 } \\ n_{13}&= \frac{16g_3 v_0^5 +4v_2 v_1 v_0^2 -v_1^3 -8v_3 v_0^4 }{16v_0^5 } \\ n_{14}&= \frac{128g_3 v_0^7 -64v_4 v_0^6 +32v_3 v_1 v_0^4 +16v_0^4 v_2^2 -24v_1^2 v_2 v_0^2 +5v_1^4 }{128v_0^7 } \end{aligned}$$

$$\begin{aligned} a_{i0}&= \frac{n_{i0} }{2\left( {1-B_1 } \right)} \\ a_{ij}&= \frac{1}{2}\left[ {\frac{n_{ij} }{\left( {1-B_1 } \right)}+B_1 \sum _{k=j}^1 {\frac{\beta ^{k}n_{ij-k} }{\left( {1-B_1 } \right)^{k+1}}} } \right], \quad i=1,2, \quad j=1,2,3,4 \\ b_{i0}&= \sqrt{a_{i0} },\quad b_{i1} =\frac{a_{i1} }{2b_{i0} },\quad b_{i2} =\frac{4a_{i0} a_{i2} -a_{i1}^2 }{8b_{i0}^3 } \quad i=1,2 \\ b_{i3}&= \frac{8a_{i3} a_{i0}^2 -4a_{i1} a_{i2} a_{i0} +a_{i1}^3 }{16b_{i0}^5 }, \\ b_{i4}&= \frac{64a_{i4} a_{i0}^3 -32a_{i1} a_{i3} a_{i0}^2 -16a_{i2}^2 a_{i0}^2 +24a_{i1}^2 a_{i2} a_{i0} -5a_{i1}^4 }{128b_{i0}^7 } \\ a_0&= \left( {1-B_1 } \right)\left( {a_{10} -a_{20} } \right) \\ a_1&= \left( {1-B_1 } \right)\left( {a_{11} -a_{21} } \right)-B_1 \beta \left( {a_{10} -a_{20} } \right) \\ a_2&= \left( {1-B_1 } \right)\left( {a_{12} -a_{22} } \right)-B_1 \beta \left( {a_{11} -a_{21} } \right)-B_1 \beta ^{2}\left( {a_{10} -a_{20} } \right) \\ a_3&= ( {1-B_1 } )( {a_{13} -a_{23} } )-B_1 \beta ( {a_{12} -a_{22} } )-B_1 \beta ^{2}( {a_{11} -a_{21} } )-B_1 \beta ^{3}( {a_{10} -a_{20} } ) \\ a_4&= \left( {1-B_1 } \right)\left( {a_{14} -a_{24} } \right)-B_1 \beta \left( {a_{13} -a_{23} } \right)-B_1 \beta ^{2}\left( {a_{12} -a_{22} } \right)\\&-B_1 \beta ^{3}\left( {a_{11} -a_{21} } \right)-B_1 \beta ^{4}\left( {a_{10} -a_{20} } \right) \\ b_0&= \frac{1}{a_0 } \\ b_1&= \frac{-a_1 }{a_0^2 } \\ b_2&= \frac{a_1^2 -a_0 a_2 }{a_0^3 } \\ b_3&= \frac{2a_1 a_2 a_0 -a_3 a_0^2 -a_1^3 }{a_0^4 } \\ b_4&= \frac{2a_1 a_3 a_0^2 -a_4 a_0^3 +a_2^2 a_0^2 -3a_0 a_2 a_1^2 +a_1^4 }{a_0^5 } \\ c_0&= \frac{b_0 }{B_4 } \\ c_1&= \frac{b_1 B_4 +b_0 \beta B_3 }{B_4^2 } \\ c_2&= \frac{b_2 B_4^2 +b_1 \beta B_3 B_4 +b_0 \beta ^{2}B_3 B_2 }{B_4^3 } \\ c_3&= \frac{b_3 B_4^3 +b_2 \beta B_3 B_4^2 +b_1 \beta ^{2}B_3 B_2 B_4 +b_0 \beta ^{3}B_3 B_2^2 }{B_4^4 } \\ c_4&= \frac{b_4 B_4^4 +b_3 \beta B_3 B_4^3 +b_2 \beta ^{2}B_3 B_2 B_4^2 +b_1 \beta ^{3}B_3 B_2^2 B_4 +b_0 \beta ^{4}B_3 B_2^3 }{B_4^5 } \\ d_{i0}&= \left( {1-B_1 } \right)a_{i0} -1 \\ d_{i1}&= \left( {1-B_1 } \right)a_{i1} -B_1 \beta a_{i0} \end{aligned}$$

$$\begin{aligned} d_{i2}&= \left( {1-B_1 } \right)a_{i2} -B_1 \beta a_{i1} -B_1 \beta ^{2}a_{i0} \quad \quad , i = 1,2 \\ d_{i3}&= \left( {1-B_1 } \right)a_{i3} -B_1 \beta a_{i2} -B_1 \beta ^{2}a_{i1} -B_1 \beta ^{3}a_{i0} \\ d_{i4}&= \left( {1-B_1 } \right)a_{i4} -B_1 \beta a_{i3} -B_1 \beta ^{2}a_{i2} -B_1 \beta ^{3}a_{i1} -B_1 \beta ^{4}a_{i0} \\ d_0&= d_{10} d_{20} \\ d_1&= d_{10} d_{21} +d_{11} d_{20} \\ d_2&= d_{10} d_{22} +d_{11} d_{21} +d_{12} d_{20} \\ d_3&= d_{10} d_{23} +d_{11} d_{22} +d_{12} d_{21} +d_{13} d_{20} \\ d_4&= d_{10} d_{24} +d_{11} d_{23} +d_{12} d_{22} +d_{13} d_{21} +d_{14} d_{20} \\ \theta _{i0}&= b_0 d_{i0} \\ \theta _{i1}&= b_0 d_{i1} +b_1 d_{i0} \\ \theta _{i2}&= b_0 d_{i2} +b_1 d_{i1} +b_2 d_{i0}, \quad i = 1,2 \\ \theta _{i3}&= b_0 d_{i3} +b_1 d_{i2} +b_2 d_{i1} +b_3 d_{i0} \\ \theta _{i4}&= b_0 d_{i4} +b_1 d_{i3} +b_2 d_{i2} +b_3 d_{i1} +b_4 d_{i0} \\ \theta _{m0}&= d_0 c_0 \\ \theta _{m1}&= d_0 c_1 +d_1 c_0 \\ \theta _{m2}&= d_0 c_2 +d_1 c_1 +d_2 c_0 \\ \theta _{m3}&= d_0 c_3 +d_1 c_2 +d_2 c_1 +d_3 c_0 \\ \theta _{m4}&= d_0 c_4 +d_1 c_3 +d_2 c_2 +d_3 c_1 +d_4 c_0 \\ \sigma _0&= B_4 b_0 \\ \sigma _1&= B_4 b_1 -B_3 \beta b_0 \\ \sigma _2&= B_4 b_2 -B_3 \beta \left( {b_1 +\beta b_0 } \right) \\ \sigma _3&= B_4 b_3 -B_3 \beta \left( {b_2 +\beta b_1 +\beta ^{2}b_0 } \right) \\ \sigma _4&= B_4 b_4 -B_3 \beta \left( {b_3 +\beta b_2 +\beta ^{2}b_1 +\beta ^{3}b_0 } \right) \\ u_{i0}&= \sigma _0 b_{i0} \\ u_{i1}&= \sigma _0 b_{i1} +\sigma _1 b_{i0} \\ u_{i2}&= \sigma _0 b_{i2} +\sigma _1 b_{i1} +\sigma _2 b_{i0} \\ u_{i3}&= \sigma _0 b_{i3} +\sigma _1 b_{i2} +\sigma _2 b_{i1} +\sigma _3 b_{i0} \\ u_{i2}&= \sigma _0 b_{i4} +\sigma _1 b_{i3} +\sigma _2 b_{i2} +\sigma _3 b_{i1} +\sigma _4 b_{i0} \\ v_{10}&= b_{10} \theta _{20} \\ v_{11}&= b_{10} \theta _{21} +b_{11} \theta _{20} \\ v_{12}&= b_{10} \theta _{22} +b_{11} \theta _{21} +b_{12} \theta _{20} \\ v_{13}&= b_{10} \theta _{23} +b_{11} \theta _{22} +b_{12} \theta _{21} +b_{13} \theta _{20} \\ v_{14}&= b_{10} \theta _{24} +b_{11} \theta _{23} +b_{12} \theta _{22} +b_{13} \theta _{21} +b_{14} \theta _{20} \\ v_{20}&= b_{20} \theta _{10} \\ v_{21}&= b_{20} \theta _{11} +b_{21} \theta _{10} \\ v_{22}&= b_{20} \theta _{12} +b_{21} \theta _{11} +b_{22} \theta _{10} \\ v_{23}&= b_{20} \theta _{13} +b_{21} \theta _{12} +b_{22} \theta _{11} +b_{23} \theta _{10} \\ v_{24}&= b_{20} \theta _{14} +b_{21} \theta _{13} +b_{22} \theta _{12} +b_{23} \theta _{11} +b_{24} \theta _{10} \end{aligned}$$