Abstract
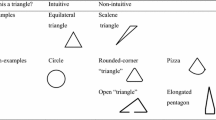
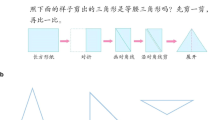
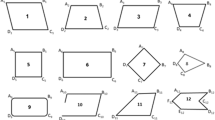
This study presents a characterization of prospective early childhood teachers’ (ECEPTs) and prospective elementary school mathematics teachers’ (EMEPTs) concept images and concept definitions of triangles through a defining task and an example generation task. Data consisted of 62 EMEPTs’ and 72 ECEPTs’ written statements for the definition of a triangle, drawings for examples and non-examples of triangles, and written reasons for drawings. The results showed that most of the prospective teachers wrote inappropriate statements for the definitions of a triangle by using necessary but not sufficient conditions or using neither necessary nor sufficient conditions with frequent inaccurate terminology usage. The appropriate statements for the definition of a triangle included necessary and sufficient conditions, but were mostly considerably not minimal and/or included inappropriate mathematical terminology. A very large portion of the examples drawn by the prospective teachers consisted of acute triangles with typical positions rather than right and obtuse triangles, which can be evaluated as the indication of prototypical concept images. Drawings of non-triangles also revealed that the prospective teachers mostly drew non-triangular non-examples that can be immediately accepted as non-triangles with the lack of a relatively long list of missing critical attributes, but they provided a small number of triangular non-examples that bear significant similarity to valid examples of a triangle. This result indicates that the prospective teachers’ concept images regarding non-triangles also formed by intuitive non-examples which can be considered as prototypes for non-triangles.


Similar content being viewed by others
References
Alatorre, S., & Sáiz, M. (2009). Triangles’ prototypes and teachers’ conceptions. In M. Tzekaki, M. Kaldrimidou, & H. Sakonidis (Eds.), Proceedings of the 33rd PME International Conference (Vol. 2, pp. 25–32). Thessaloniki, Greece: PME.
Alcock, L., & Simpson, A. (2017). Interactions between defining, explaining and classifying: The case of increasing and decreasing sequences. Educational Studies in Mathematics, 94(1), 5–19.
Ball, D. L., Thames, M. H., & Phelps, G. (2008). Content knowledge for teaching: what makes it special? Journal of Teacher Education, 59(5), 389–407.
Bills, L., Dreyfus, T., Mason, J., Tsamir, P., Watson, A., & Zaslavsky, O. (2006). Exemplification in mathematics education. In J. Novotna (Ed.), Proceedings of the 30th PME International Conference. Prague, Czech: PME.
Burger, W. F., & Shaughnessy, J. M. (1986). Characterizing the van Hiele levels of development in geometry. Journal for Research in Mathematics Education, 17(1), 31–48.
Clements, D. H., Swaminathan, S., Hannibal, M. A. Z., & Sarama, J. (1999). Young children’s concepts of shape. Journal for Research in Mathematics Education, 30, 192–212.
Cunningham, R. F., & Roberts, A. (2010). Reducing the mismatch of geometry concept definitions and concept images held by pre-service teachers. IUMPST: The Journal, 1, 1–17.
de Villiers, M., Govender, R., & Patterson, N. (2009). Defining in geometry. In T. V. Craine & R. Rubenstein (Eds.), Understanding geometry for a changing world, seventy-first yearbook (pp. 189–203). Reston, VA: NCTM.
Duval, R. (1995). Geometrical pictures: Kinds of representation and specific processing. In R. Sutherland & J. Mason (Eds.), Exploiting mental imagery with computers in mathematics education (pp. 142–157). Berlin, Germany: Springer.
Duval, R. (1998). Geometry from a cognitive point of view. In C. Mammana & V. Villani (Eds.), Perspectives on the teaching of geometry for the 21st century: An ICMI study (pp. 37–52). Dordrecht, The Netherlands: Kluwer.
Edwards, B., & Ward, M. (2008). The role of mathematical definitions in mathematics and in undergraduate mathematics courses. In M. Carlson & C. Rasmussen (Eds.), Making the connection: Research and teaching in undergraduate mathematics (pp. 221–230). Washington, DC: Mathematical Association of America.
Fischbein, E. (1987). Intuition in science and mathematics: an educational approach. Dordrecht, The Netherlands: Reidel.
Fischbein, E. (1993). The theory of figural concepts. Educational Studies in Mathematics, 24(2), 139–162.
Fischbein, E., & Nachlieli, T. (1998). Concepts and figures in geometrical reasoning. International Journal of Science Education, 20(10), 1193–1211.
Guo, J. P., & Pang, M. F. (2011). Learning a mathematical concept from comparing examples: the importance of variation and prior knowledge. European Journal of Psychology of Education, 26(4), 495–525.
Gutiérrez, A., & Jaime, A. (1999). Preservice primary teachers' understanding of the concept of altitude of a triangle. Journal of Mathematics Teacher Education, 2(3), 253–275.
Hannibal, M. Z. (1999). Young children’s developing understanding of geometric shapes. Teaching Children Mathematics, 5(6), 353–358.
Hershkowitz, R. (1987). The acquisition of concepts and misconceptions in basic geometry—or when a little learning is a dangerous thing. In J. D. Novak (Ed.), Proceedings of the second international seminar on misconceptions and educational strategies in science and mathematics (Vol. 3, pp. 236–251). Ithaca, NY: Cornell University.
Hershkowitz, R. (1989). Visualization in geometry: Two sides of the coin. Focus on Learning Problems in Mathematics, 11(1), 61–76.
Johnson, H. L., Blume, G. W., Shimizu, J. K., Graysay, D., & Konnova, S. (2014). A teacher’s conception of definition and use of examples when doing and teaching mathematics. Mathematical Thinking and Learning, 16(4), 285–311.
Jones, K. (2000). Teacher knowledge and professional development in geometry. Proceedings of the British society for research into learning mathematics, 20(3), 109–114.
Kaur, H. (2015). Two aspects of young children’s thinking about different types of dynamic triangles: Prototypicality and inclusion. ZDM, 47(3), 407–420.
Leikin, R., & Zazkis, R. (2010). On the content-dependence of prospective teachers’ knowledge: A case of exemplifying definitions. International Journal of Mathematical Education in Science and Technology, 41(4), 451–466.
Linchevsky, L., Vinner, S., & Karsenty, R. (1992). To be or not to be minimal? Student teachers' views about definitions in geometry. In In W. Geeslin & K. Graham (Eds.), Proceedings of the 16th international conference for the psychology of mathematics education (Vol. 2, pp. 48–55). Durham, England: NH.
Miles, M. B., & Huberman, A. M. (1994). Qualitative data analysis. Thousand Oaks, CA: Sage Publications.
Miyakawa, T. (2017). Comparative analysis on the nature of proof to be taught in geometry: The cases of French and Japanese lower secondary schools. Educational Studies in Mathematics, 94, 37–54.
Petty, O. S., & Jansson, L. C. (1987). Sequencing examples and nonexamples to facilitate concept attainment. Journal for Research in Mathematics Education, 18(2), 112–125.
Shulman, L. S. (1986). Those who understand: Knowledge growth in teaching. Educational Researcher, 15(2), 4–14.
Tall, D., & Vinner, S. (1981). Concept image and concept definition in mathematics with particular reference to limits and continuity. Educational Studies in Mathematics, 12(2), 151–169.
Tsamir, P., Tirosh, D., Levenson, E., Barkai, R., & Tabach, M. (2015). Early-years teachers’ concept images and concept definitions: triangles, circles, and cylinders. ZDM, 47, 497–509.
Tsamir, P., Tirosh, S., & Levenson, E. (2008). Intuitive non examples: The case of triangles. Educational Studies in Mathematics, 69(2), 81–95.
Ubuz, B., & Aydın, U. (2018). Geometry knowledge test about triangles: Evidence on validity and reliability. ZDM, 50(4), 659–673.
Usiskin, Z., Griffin, J., Witonsky, D., & Willmore, E. (2008). The classification of quadrilaterals: a study in definition. Charlotte, NC: Information Age Publishing.
Van der Sandt, S., & Nieuwoudt, H. D. (2003). Grade 7 teachers' and prospective teachers' content knowledge of geometry. South African Journal of Education, 23(3), 199–205.
Van Dormolen, J., & Zaslavsky, O. (2003). The many facets of a definition: The case of periodicity. The Journal of Mathematical Behavior, 22(1), 91–106.
Vinner, S. (1983). Concept definition, concept image and the notion of function. International Journal of Mathematical Education in Science and Technology, 14(3), 293–305.
Vinner, S. (1991). The role of definitions in the teaching and learning of mathematics. In D. Tall (Ed.), Advanced mathematical thinking (pp. 65–81). Dordrecht, The Netherlands: Kluwer.
Vinner, S. (2011). The role of examples in the learning of mathematics and in everyday thought processes. ZDM, 43(2), 247–256.
Vinner, S., & Hershkowitz, R. (1980). Concept images and some common cognitive paths in the development of some simple geometric concepts. In R. Karplus (Ed.), Proceedings of the 4th PME International Conference (pp. 177–184). Berkeley, CA: Berkley.
Vinner, S., Linchevski, L., & Karsenty, R. (1993). How much information should include a geometrical definition? Zentralblatt für Didaktik der Mathematik, 25, 164–170.
Vygotsky, L. S. (1978). Mind in society. Cambridge, MA: Harvard University Press.
Ward, R. A. (2004). An investigation of K-8 preservice teachers' concept images and mathematical definitions of polygons. Issues in Teacher Education, 13(2), 39–56.
Watson, A., & Mason, J. (2005). Mathematics as a constructive activity: Learners generating examples. Mahwah, NJ: Lawrence Erlbaum Associates.
Weisstein, E. W. (2020). MathWorld-A Wolfram Web: Polygon. Retrieved March 24, 2020 from http://mathworld.wolfram.com/Polygon.html.
Winicki-Landman, G., & Leikin, R. (2000). On equivalent and non-equivalent definitions: Part 1. For the Learning of Mathematics, 20(1), 17–21.
Yin, R. K. (2009). Case study research: Design and methods. Thousand Oaks, CA: Sage.
Zandieh, M., & Rasmussen, C. (2010). Defining as a mathematical activity: A framework for characterizing progress from informal to more formal ways of reasoning. The Journal of Mathematical Behavior, 29(2), 57–75.
Zaslavsky, O., & Shir, K. (2005). Students' conceptions of a mathematical definition. Journal for Research in Mathematics Education, 36(4), 317–346.
Zazkis, R., & Leikin, R. (2007). Generating examples: From pedagogical tool to a research tool. For the Learning of Mathematics, 27(2), 15–21.
Zazkis, R., & Leikin, R. (2008). Exemplifying definitions: a case of a square. Educational Studies in Mathematics, 69(2), 131–148.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Ulusoy, F. Prospective Early Childhood and Elementary School Mathematics Teachers’ Concept Images and Concept Definitions of Triangles. Int J of Sci and Math Educ 19, 1057–1078 (2021). https://doi.org/10.1007/s10763-020-10105-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10763-020-10105-6