Abstract
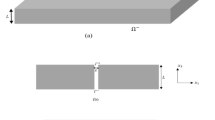
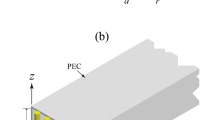
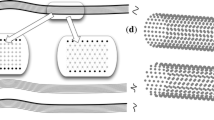
In this paper we evaluate methods for calculating dispersion relations for waves with wavelengths of the order of hundreds of nanometres propagating in square waveguides with imperfectly conducting walls. The methods considered here are based on those used previously for rectangular dielectric waveguides.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
T. W. Ebbesen, H. E. Lezec, H. F. Ghaemi, T. Thio and P. A. Wolff, “Extraordinary optical transmission through sub-wavelength hole arrays,” Nature 391, 667–669 (1998).
N.W. Ashcroft and N.D. Mermin, Solid State Physics (Holt, Rinehart and Winston, New York, 1976), Chap. 1.
J.A. Stratton, Electromagnetic Theory, (McGraw-Hill, New York, 1941), p. 526.
P.B. Catrysse, H. Shin and S. Fan, “Propagating modes in subwavelength cylindrical holes,” J. Vac. Sci. Technol. B 23/6, 2675–2678 (2005).
L. Novotny and C. Hafner, “Light propagation in a cylindrical waveguide with a complex metallic dielectric function,” Phys. Rev. E 50/5, 4094–4106 (1994).
E.A. Marcatili, “Dielectric rectangular waveguide and directional coupler for integrated optics,” Bell System Tech. J. 48, 2071–2102 (1969).
V.J. Menon, S. Bhattacharjee and K.K. Dey, “The rectangular dielectric waveguide revisited,” Optics Communications 85, 393–396 (1991).
A. S. Sudbø, “Why are accurate computations of mode fields in rectangular dielectric waveguides difficult?” J. Lightwave Technology 10/4, 418–419 (1992).
R.M. Knox and P.P. Tulios Proc. of the MRI Symposium on Submillimeter Waves, ed. J. Fox (Brooklyn: Polytechnic Press 1970) p. 497.
S.P. Pogossian, H. Le Gall, J. Gieraltowski and J. Loaec, “Determination of the parameters of rectangular dielectric waveguides by new effective index methods,” J. Modern Optics 42/2, 403–409 (1995).
E.A. Marcatili and A.A. Hardy, “The azimuthal effective-index method,” IEEE J Quantum Electonics 24/5, 766–774 (1988).
J.E. Goell, “A circular-harmonic computer analysis of rectangular dielectric waveguides,” Bell System Tech. J. 48, 2133–2160 (1969).
S.M. Saad, “Review of numerical methods for the analysis of arbitrarily-shaped microwave and optical dielectric waveguides,” IEEE Trans. Microwave Theory and Techniques 33/10, 894–897 (1985).
R. Gordon and A.G. Brolo, “Increased cut-off wavelength for a subwavelength hole in a real metal,” Optics Express 13/6, 1933–1938 (2005).
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Brand, G.F. LIGHTWAVE PROPAGATION IN SUBWAVELENGTH HOLES. Int J Infrared Milli Waves 27, 1445–1456 (2006). https://doi.org/10.1007/s10762-006-9148-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10762-006-9148-x