Abstract
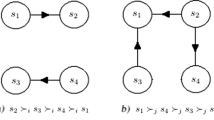
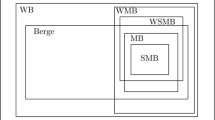
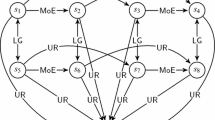
Explicit matrix representations of solution concepts in a graph model of a multiple-decision-maker conflict with preference uncertainty are developed. In a graph model, the relative preferences of each DM over the available states are crucial in determining which states are stable according to any stability definition (solution concept). Unfortunately, it is often difficult to obtain accurate preference information in practical cases, so models that allow preference uncertainty can be very useful. In this work, stability definitions are extended to apply to graph models with this feature. The extension is easiest to implement using the matrix representation of a conflict model, which was developed to ease the coding of logically-defined stability definitions. Another benefit of matrix representation is that it facilitates modification and extension of the definitions.
Similar content being viewed by others
References
Brams SJ, Wittman D (1981) Nonmyopic equilibria in 2 × 2 games. Confl Manag Peace Sci 6(1): 39–62
Brams SJ (1993) Theory of moves. Combridge University Press, Cambridge
Cohn H, Kleinberg R, Szegedy B, Umans C (2005) Group-theoretic algorithms for matrix multiplication. In: Proceedings of the 46th annual symposium on foundations of computer science, pp 379–388
Coppersmith D, Winograd S (1990) Matrix multiplication via arithmetic programming. J Symb Comput 9: 251–280
Fang L, Hipel KW, Kilgour DM (1993) Interactive decision making: the graph model for conflict resolution. Wiley, New York
Fang L, Hipel KW, Wang L (2002) Gisborne water export conflict study. In: Proceedings of 3rd international conference on water resources environment research 1:432–436
Fang L, Hipel KW, Kilgour DM, Peng X (2003a) A decision support system for interactive decision making, part 1: model formulation. IEEE Trans Syst Man Cybern Part C Appl Rev 33(1): 42–55
Fang L, Hipel KW, Kilgour DM, Peng X (2003b) A decision support system for interactive decision making, part 2: analysis and output interpretation. IEEE Trans Syst Man Cybern Part C Appl Rev 33(1): 56–66
Fischer GW, Jia J, Luce MF (2000a) Attribute conflict and preference uncertainty: the randMAU model. Manag Sci 46(5): 669–684
Fischer GW, Luce MF, Jia J (2000b) Attribute conflict and preference uncertainty: effects on judgment time and error. Manag Sci 46(1): 88–103
Fraser NM, Hipel KW (1979) Solving complex conflicts. IEEE Trans Syst Man Cybern 9: 805–817
Fraser NM, Hipel KW (1984) Conflict analysis: models and resolution. Wiley, New York
Hamouda L, Kilgour DM, Hipel KW (2004) Strength of preference in the graph model for conflict resolution. Group Decis Negot 13: 449–462
Hamouda L, Kilgour DM, Hipel KW (2006) Strength of preference in graph models for multiple-decision-maker conflicts. Appl Math Comput 179: 314–327
Howard N (1971) Paradoxes of rationality: theory of metagames and political behavior. MIT press, Cambridge
Kilgour DM, Hipel KW, Fraser NM (1984) Solution concepts in non-cooperative games. Large Scale Syst 6: 49–71
Kilgour DM (1985) Anticipation and stability in two-person noncooperative games. Dynamic model of international conflict. Lynne Rienner Press, Boulder, pp 26–51
Kilgour DM, Hipel KW, Fang L (1987) The graph model for conflicts. Automatica 23: 41–55
Kilgour DM, Hipel KW (2005) The graph model for conflict resolution: past, present, and future. Group Decis Negot 14: 441–460
Li KW, Hipel KW, Kilgour DM, Fang L (2004) Preference uncertainty in the graph model for conflict resolution. IEEE Trans Syst Man Cybern-Part A: Syst Hum 34: 507–520
Li KW, Kilgour DM, Hipel KW (2005) Status quo analysis in the graph model for conflict resolution. J Oper Res Soc 56: 699–707
Nash JF (1950) Equilibrium points in n-person games. In: Proceedings of the national academy of sciences 36:48–49
Nash JF (1951) Noncooperative games. Ann Math 54(2): 286–295
Neumann J, Morgenstern O (1944) Theory of games and economic behavior. Princeton University Press, Princeton
Stackelberg H (1934) Marktform und gleichgewicht. Springer, Vienna
Xu H, Hipel KW, Kilgour DM (2007a) Matrix representation of conflicts with two decision-makers. In: Proceedings of the 2007 IEEE international conference on systems, man and cybernetics, pp 1764–1769
Xu H, Kilgour DM, Hipel KW (2007b) Matrix representation of solution concepts in graph models for two decision-makers with preference uncertainty. Dyn Continuous Discret Impuls Syst 14(1): 703–707
Xu H, Hipel KW, Kilgour DM (2009a) Matrix representation of solution concepts in multiple decision maker graph models. IEEE Trans Syst Man Cybern Part A Syst Hum 39(1): 96–108
Xu H, Li KW, Hipel KW, Kilgour DM (2009) A matrix approach to status quo analysis in the graph model for conflict resolution. Appl Math Comput 212(2): 470–480
Xu H, Hipel KW, Kilgour DM (2009) Multiple-level hierarchies of preference in interactive strategic decisions. Discrete Appl Math 157: 3300–3313
Zagare FC (1984) Limited-move equilibria in games 2 × 2 games. Theory Decis 16: 1–19
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Xu, H., Kilgour, D.M. & Hipel, K.W. Matrix Representation of Conflict Resolution in Multiple-Decision-Maker Graph Models with Preference Uncertainty. Group Decis Negot 20, 755–779 (2011). https://doi.org/10.1007/s10726-010-9188-4
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10726-010-9188-4