Skip to main content
SpringerLink
Log in

Extended phase space thermodynamics and \(P-V\) criticality of charged black holes in Brans–Dicke theory

  • Research Article
  • Published:
General Relativity and Gravitation Aims and scope Submit manuscript

Abstract

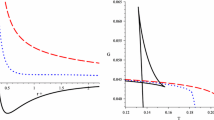
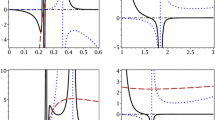
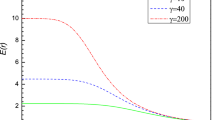
Motivated by conformal relation between dilaton gravity and Brans–Dicke theory, in this paper, we are taking into account extended phase space thermodynamics to investigate phase transition of charged black holes. We regard spherically symmetric charged black hole solutions in the presence of a scalar field in both Einstein and Jordan frames and calculate related conserved and thermodynamic quantities. Then, we study the analogy of the black hole solution with the Van der Waals liquid–gas system in the extended phase space by considering the cosmological constant proportional to thermodynamical pressure. We obtain critical values of thermodynamic coordinates and plot \(P-V\) and \(G-T\) diagrams to study the phase transition points and compare the results of dilaton gravity and Brans–Dicke theory.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10

Similar content being viewed by others

References

  1. Gibbons, G.W., Maeda, K.: Nucl. Phys. B 298, 741 (1988)

    Article  MathSciNet  ADS  Google Scholar 

  2. Garfinkle, D., Horowitz, G.T., Strominger, A.: Phys. Rev. D 43, 3140 (1991)

    Article  MathSciNet  ADS  Google Scholar 

  3. Chan, K.C.K., Horne, J.H., Mann, R.B.: Nucl. Phys. B 447, 441 (1995)

    Article  MATH  MathSciNet  ADS  Google Scholar 

  4. Chiba, T., Soda, J.: Prog. Theor. Phys. 96, 567 (1996)

    Article  ADS  Google Scholar 

  5. Cai, R.G., Myung, Y.S.: Phys. Rev. D 56, 3466 (1997)

    Article  MathSciNet  ADS  Google Scholar 

  6. Dehghani, M.H., Pakravan, J., Hendi, S.H.: Phys. Rev. D 74, 104014 (2006)

    Article  MathSciNet  ADS  Google Scholar 

  7. Hendi, S.H.: J. Math. Phys. 49, 082501 (2008)

    Article  MathSciNet  ADS  Google Scholar 

  8. Hendi, S.H., Katebi, R.: Eur. Phys. J. C 72, 2235 (2012)

    Article  ADS  Google Scholar 

  9. Clifton, T., Ferreira, P.G., Padilla, A., Skordis, C.: Phys. Rep. 513, 1 (2012)

    Article  MathSciNet  ADS  Google Scholar 

  10. Brans, C., Dicke, R.: Phys. Rev. 124, 925 (1961)

    Article  MATH  MathSciNet  ADS  Google Scholar 

  11. Scheel, M.A., Shapiro, S.L., Teukolsky, S.A.: Phys. Rev. D 51, 4208 (1995)

    Article  MathSciNet  ADS  Google Scholar 

  12. Scheel, M.A., Shapiro, S.L., Teukolsky, S.A.: Phys. Rev. D 51, 4236 (1995)

    Article  MathSciNet  ADS  Google Scholar 

  13. Kang, G.: Phys. Rev. D 54, 7483 (1996)

    Article  MathSciNet  ADS  Google Scholar 

  14. de Oliveira, H.P., Cheb-Terrab, E.S.: Class. Quantum Gravit. 13, 425 (1996)

    Article  MATH  ADS  Google Scholar 

  15. Hawking, S.W.: Commun. Math. Phys. 25, 167 (1972)

    Article  MathSciNet  ADS  Google Scholar 

  16. Teitelboim, Phys: Lett. B 158, 293 (1985)

    Article  ADS  Google Scholar 

  17. Creighton, J., Mann, R.B.: Phys. Rev. D 52, 4569 (1995)

    Article  MathSciNet  ADS  Google Scholar 

  18. Padmanabhan, T.: Class. Quantum Gravit. 19, 5387 (2002)

    Article  MATH  MathSciNet  ADS  Google Scholar 

  19. Kastor, D., Ray, S., Traschen, J.: Class. Quantum Gravit. 26, 195011 (2009)

    Article  MathSciNet  ADS  Google Scholar 

  20. Delsate, T., Mann, R.B.: J. High Energy Phys. 02, 070 (2015)

    Article  MathSciNet  ADS  Google Scholar 

  21. Rajagopal, A., Kubiznak, D., Mann, R.B.: Phys. Lett. B 737, 277 (2014)

  22. Dolan, B.P.: Class. Quantum Gravit. 28, 125020 (2011)

    Article  MathSciNet  ADS  Google Scholar 

  23. Kubiznak, D., Mann, R.B.: J. High Energy Phys. 07, 033 (2012)

    Article  MathSciNet  ADS  Google Scholar 

  24. Dolan, B.P.: Class. Quantum Gravit. 28, 235017 (2011)

    Article  MathSciNet  ADS  Google Scholar 

  25. Hendi, S.H., Vahidinia, M.H.: Phys. Rev. D 88, 084045 (2013)

    Article  ADS  Google Scholar 

  26. Hendi, S.H., Panahiyan, S., Eslam Panah, B.: Int. J. Mod. Phys. D (accepted). arXiv:1410.0352

  27. Hendi, S.H., Panahiyan, S., Momennia, M.: Int. J. Mod. Phys. D (accepted). arXiv:1503.03340

  28. Hawking, S.W., Page, D.N.: Commun. Math. Phys. 87, 577 (1983)

    Article  MathSciNet  ADS  Google Scholar 

  29. Chamblin, A., Emparan, R., Johnson, C., Myers, R.: Phys. Rev. D 60, 64018 (1999)

    Article  MathSciNet  ADS  Google Scholar 

  30. Niu, C., Tian, Y., Wu, X.N.: Phys. Rev. D 85, 24017 (2012)

    Article  ADS  Google Scholar 

  31. Sheykhi, A.: Phys. Rev. D 76, 124025 (2007)

    Article  MathSciNet  ADS  Google Scholar 

  32. Hansen, J., Yeom, D.H.: J. High Energy Phys. 10, 040 (2014)

    Article  MathSciNet  ADS  Google Scholar 

  33. Hwang, D.I., Yeom, D.H.: Class. Quantum Gravit. 27, 205002 (2010)

    Article  MathSciNet  ADS  Google Scholar 

  34. Dolan, B.P.: Mod. Phys. Lett. A 30, 1540002 (2015)

    Article  MathSciNet  ADS  Google Scholar 

  35. Cvetic, M., Gibbons, G.W., Kubiznak, D., Pope, C.N.: Phys. Rev. D 84, 024037 (2011)

    Article  ADS  Google Scholar 

Download references

Acknowledgments

We would like to thank the anonymous referees for valuable suggestions and Shahram Panahiyan for reading the manuscript. We also wish to thank the Shiraz University Research Council. This work has been supported financially by Research Institute for Astronomy and Astrophysics of Maragha, Iran.

Author information

Authors and Affiliations

  1. Physics Department and Biruni Observatory, College of Sciences, Shiraz University, Shiraz, 71454, Iran

    S. H. Hendi & Z. Armanfard

  2. Research Institute for Astrophysics and Astronomy of Maragha (RIAAM), P.O. Box 55134-441, Maragha, Iran

    S. H. Hendi

Authors
  1. S. H. Hendi
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Z. Armanfard
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to S. H. Hendi.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Hendi, S.H., Armanfard, Z. Extended phase space thermodynamics and \(P-V\) criticality of charged black holes in Brans–Dicke theory. Gen Relativ Gravit 47, 125 (2015). https://doi.org/10.1007/s10714-015-1965-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s10714-015-1965-6

Keywords

Search

Navigation