Skip to main content
SpringerLink
Log in

Curves in the Minkowski plane and their contact with pseudo-circles

  • Original Paper
  • Published:
Geometriae Dedicata Aims and scope Submit manuscript

Abstract

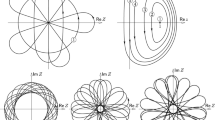
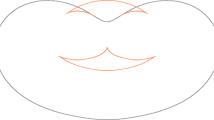
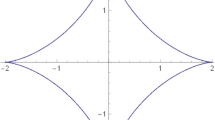
We study the caustic, evolute, Minkowski symmetry set and parallels of a smooth and regular curve in the Minkowski plane.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Arnol’d V.I.: Wave front evolution and equivariant Morse Lemma. Comm. Pure Appl. Math. 29, 557–582 (1976)

    Article  MathSciNet  MATH  Google Scholar 

  2. Arnol’d, V.I., Gusein-Zade, S.M., Varchenko, A.N.: Singularities of Differentiable Maps, vol. I. Birkhäuser (1986)

  3. Bruce J.W.: Wavefronts and parallels in Euclidean space. Math. Proc. Camb. Phil. Soc. 93, 323–333 (1983)

    Article  MathSciNet  MATH  Google Scholar 

  4. Bruce J.W.: A note on first order differential equations of degree greater than one and wavefront evolution. Bull. Lond. Math. Soc. 16, 139–144 (1984)

    Article  MathSciNet  MATH  Google Scholar 

  5. Bruce J.W., Giblin P.J.: Curves and Singularities. Cambridge University Press, Cambridge (1984)

    MATH  Google Scholar 

  6. Dara L.: Singularités génériques des équations differentielles multiformes. Bol. Soc. Brasil Math. 6, 95–128 (1975)

    Article  MathSciNet  MATH  Google Scholar 

  7. Davydov, A.A.: Qualitative Control Theory. Translations of Mathematical Monographs 142. AMS, Providence RI (1994)

  8. Giblin P.J., Brassett S.A.: Local symmetry of plane curves. Amer. Math. Mon. 92, 689–707 (1985)

    Article  MathSciNet  MATH  Google Scholar 

  9. Khesin B., Tabachnikov S.: Pseudo-Riemannian geodesics and billiards. Adv. Math. 221, 1364–1396 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  10. O’Neill B.: Semi-Riemannian Geometry. With applications to relativity. Pure and Applied Mathematics. Academic Press, London (1983)

    Google Scholar 

  11. Öztekin H.B., Ergüt M.: Eigenvalue equations for Nonnull curve in Minkowski plane. Int. J. Open Probl. Compt. Math. 3, 467–480 (2010)

    Google Scholar 

  12. Siddiqi, K., Pizer, S.M. (eds.): Medial Representations Mathematics, Algorithms and Applications. Computational Imaging and Vision, vol. 37 (2008)

  13. Tabachnikov S.: Parametrized plane curves, Minkowski caustics, Minkowski vertices and conservative line fields. Enseign. Math. 43, 3–26 (1997)

    MathSciNet  MATH  Google Scholar 

  14. Tari F.: Caustics of surfaces in the Minkowski 3-space. Q. J. Math. 00, 1–21 (2010). doi:10.1093/qmath.laq030

    Google Scholar 

Download references

Author information

Author notes

  1. Farid Tari

    Present address: Instituto de Ciências Matemáticas e de Computação—USP, Avenida Trabalhador São-Carlense, 400-Centro, São Carlos, SP, CEP 13566-590, Brazil

Authors and Affiliations

  1. Department of Mathematical Sciences, Science Laboratories, Durham University, South Road, Durham, DH1 3LE, UK

    Amani Saloom & Farid Tari

Authors
  1. Amani Saloom
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Farid Tari
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Farid Tari.

Additional information

Amani Saloom was supported by a PhD grant from King Abdulaziz University.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Saloom, A., Tari, F. Curves in the Minkowski plane and their contact with pseudo-circles. Geom Dedicata 159, 109–124 (2012). https://doi.org/10.1007/s10711-011-9649-1

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10711-011-9649-1

Keywords

Mathematics Subject Classification (2000)

Search

Navigation